倒角方形桥塔驰振特性分析及控制措施研究
孙 璐
(四川省交通运输厅公路规划勘察设计研究院,四川成都 610041)
1 研究背景
桥塔是桥梁结构体系的重要组成部分,高度会随着桥跨的增加而显著增大。对于大跨桥梁中的桥塔结构,当其截面形式较钝、结构较柔、质量轻、阻尼低时,将极易出现驰振问题[1]。驰振是一种经典的柔性结构气动失稳现象,是一种发散性的自激振动,具有低频率和横风向大振幅的特点[2]。Novak[3-4]对细长结构横风向驰振问题进行了理论研究;顾明等[5]以某一斜拉桥的初步设计方案为例,利用平均法推导了具有分段变截面的斜拉桥桥塔驰振响应计算公式;梁枢国等[6]在相关风洞试验提供的气动参数基础上,分析了正方形和长宽比为2的矩形截面高耸结构稳态响应计算公式及驰振发生与突变的临界条件;李胜利等[7]针对大跨径悬索桥施工期门型变截面桥塔,提出了一种有限元与计算流体动力学CFD相结合分析高耸结构驰振的实用数值方法。
抑制结构风致振动的工程措施可分为空气动力措施和机械措施[8]。空气动力措施是通过改变原结构的外形来改善物体绕流,从而达到抑制风致振动的目的,空气动力措施能够消除激励源,具有工作可靠、不需维护、费用低的优点;机械措施主要通过外加阻尼器来提高结构阻尼,从而达到降低和抑制风致振动的目的,我国广东崖门大桥[9]就通过应用大型TMD有效地抑制了预应力混凝土桥塔的风致振动,但与空气动力措施相比,机械措施的缺点是需要维护和增加额外工程费用。
带有倒角的正方形截面形式的独柱桥塔具有施工方便、结构轻盈、外形美观等特点,在实际桥梁中有所应用,但是倒角方形桥塔的驰振临界风速较低,存在驰振安全性问题。以在建的某斜拉桥梁倒角方形桥塔为例,其最低驰振临界风速只有33 m/s,已不能满足一般的桥梁抗风要求,本文即是以上述某斜拉桥桥塔为工程背景,如图1和图2所示,以气弹模型试验为辅进行结果验证的方式,研究了该截面形式桥塔的驰振特性,并找出了两种对桥塔驰性能有改善作用的空气动力措施,即在倒角处加设圆弧形导流板或矩形垂直翼板,并进一步研究了导流板圆弧半径大小和垂直翼板透风率对驰振改善效果的影响规律。本文所得结果为研究类似截面形状塔柱结构的驰振性能及寻找相应改善措施提供了参考。
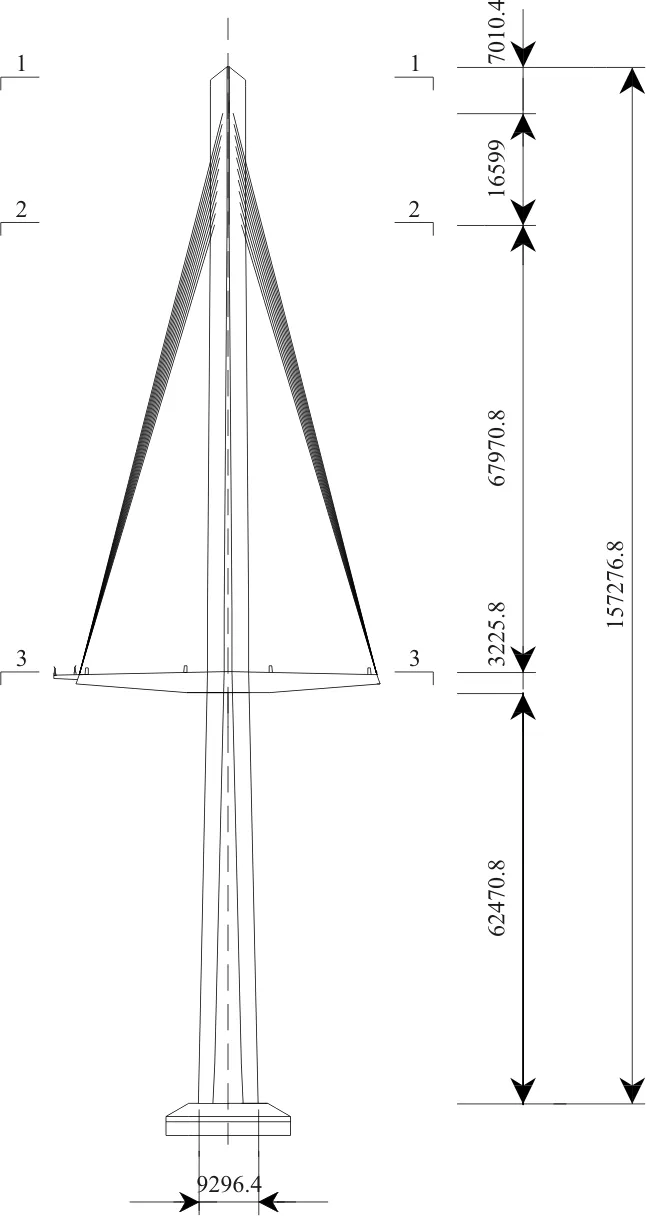
(a)立面

(b)侧面
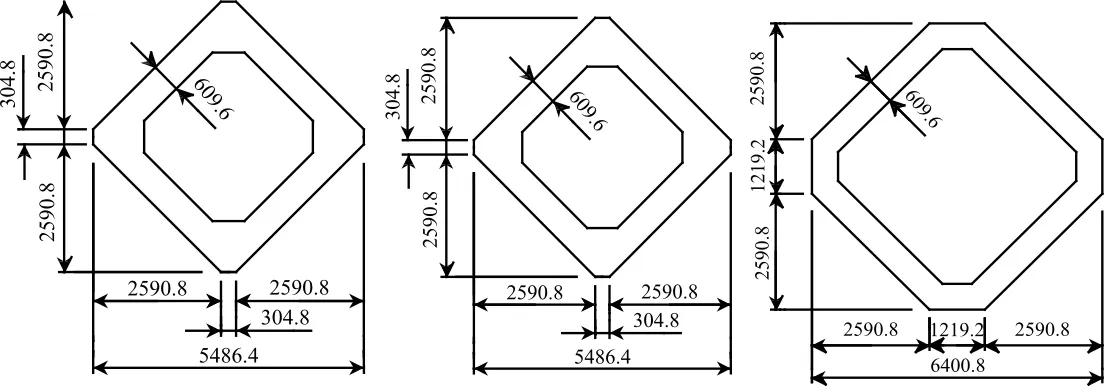
图2 西侧桥塔典型断面(单位:mm)
2 裸塔气弹模型风洞试验
根据该桥塔的具体情况,进行了裸塔状态(桥塔施工完成,尚无拉索连接)的气动弹性模型风洞试验,桥塔气弹模型的几何缩尺比为1∶80、风速比为9.1。气弹模型的刚度由金属芯梁来提供;由优质木材制作的外模来提供气动外形;不足的重量则由铅块等重物配在外模内予以调节;模型的阻尼则使用橡胶纸实现,通过反复调节橡胶纸的宽度和所放位置将阻尼值调整到一个合适值。
采用通用有限元软件ANSYS分析了原型桥塔自立状态下的动力特性,计算得到的独立裸塔固有频率特性和按相似律换算后的气弹模型试验参数见表1。对于表中频率,因为倒角方形桥塔的截面既是轴对称截面又是中心对称截面,所以桥塔每一阶的顺桥向和横桥向弯曲频率值是相等的;对于阻尼比,因为结构阻尼可以耗能,阻尼比的不同肯定会影响桥塔的驰振响应,实际桥塔阻尼比的具体值只有在建成后才可测出,对于桥梁结构阻尼比的估计值,《公路桥梁抗风设计规范》[10]中规定钢桥为0.5 %、钢混结合梁桥为1 %、混凝土桥为0.5 %,这些参考值主要是针对主梁而言,但对桥塔也具有参考意义,该在建斜拉桥梁的桥塔是混凝土材料,因此将气弹模型主要模态所对应的阻尼比,通过反复调节取至较小的0.5 %,这样得到的试验结果将是偏于安全的。风洞试验中的裸塔气弹模型如图3所示,试验来流偏安全地采用了均匀流。
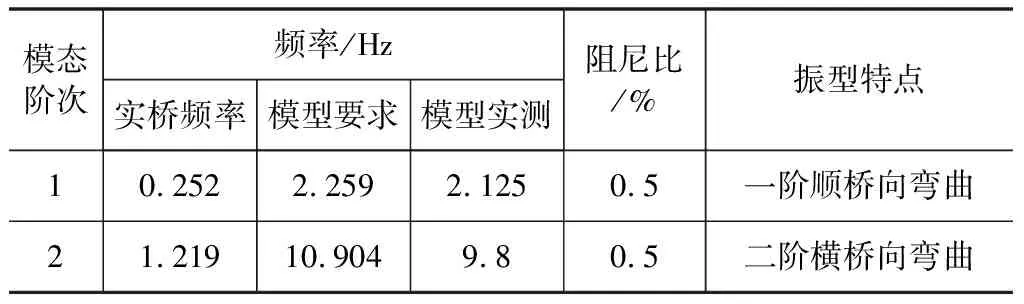
表1 桥塔气弹模型基本参数

图3 裸塔状态气动弹性模型
首先进行了-5°、0°、5°和10°风向角下,不加任何空气动力措施的桥塔风致振动试验。试验前已在在桥塔顶部布置了加速度传感器,该传感器可以测得塔顶在与0°风向角垂直方向振动的加速度均方根值,据此进而可以推算出塔顶的在该方向位移均方根值,图4不同风向角下塔顶位移随风速的变化情况,图中风速为换算后的实桥风速,位移均方根值也已通过相似准则换算至原型。

图4 各风向角下塔顶位移均方根值
通过图4可以看出,当风向角为10°时,随着风速的增加,塔顶位移基本保持为零,说明桥塔在10°风向角下具有非常良好的驰振稳定性。当风向角为-5°或5°时,在风速增大至75 m/s时,塔顶位移均方根值突然增大,有进入发射状态的趋势,说明桥塔在±5°风向角下会出现驰振失稳现象,但临界风速已经较高。而对于0°风向角的情况(此时测得的位移就是横风向位移),发现桥塔在20~28 m/s风速区间内还存在一个涡激振动锁定区间,这是通过静力试验不能发现的,值得注意;当风速升至33 m/s左右时,塔顶横风向位移出现了非常陡峭的增长趋势(横风向位移均方根值在很小的风速增长范围内便由100 mm左右增大到了800 mm左右),可以认为桥塔在33 m/s时便已经进入了振动发散状态(但图中尚有一点值得注意,就是风速继续增加至40 m/s左右时,塔顶位移反而有减小趋势,这是因为该桥塔在40 m/s风速之前又出现了第二个、第三阶振型涡激振动锁定区间,便发生了驰振和涡振耦合振动的现象,后来随着风速的增大,涡激振动现象消失,所以振动振幅相对反而变小,这并不代表桥塔在33 m/s时并未进入振动发散状态),33 m/s便是倒角方形桥塔在0°风向角处的驰振临界风速,这一风速值较低,显然不能满足一般抗风设计的要求。
为抑制桥塔的驰振,在裸塔气弹模型的上塔柱部分的4个倒角处加设圆弧形导流板和0 %透风率的矩形垂直翼板,分别如图5和图6所示。因为桥塔节段模型的缩尺比是1∶40,需按照缩尺比进行气动措施的尺寸换算,将圆弧形导流板的半径取为20 mm,而将矩形垂直翼板的高取为20 mm、厚取为2 mm。并进行加设两种气动措施后桥塔在0°风向角处的风致振动试验,为完全体现出气动措施对桥塔驰振性能的改善作用,将加设气动措施后桥塔主要模态对应的阻尼比也均调节至0.5 %(即消除结构阻尼的影响因素),试验结果如图7中所示,可以看出加设圆弧形导流板可以将桥塔驰振临界风速提高到70 m/s以上,这一风速已经很高,完全可以满足抗风设计的要求,这再次印证了圆弧形导流板可以提高倒角方形桥塔的驰振稳定性;还可以发现一点,即加设圆弧形导流板还可以有效抑制倒角方形桥塔涡激振动,静力试验是不能发现这一效果的。加设矩形垂直翼板同样可以有效提高桥塔进入驰振发射状态的临界风速、改善桥塔驰振稳定性,在50 m/s风速以下,桥塔不会再出现大幅振动现象,这和静力试验结果是完全相符的;但是,加设垂直翼板并不能有效抑制桥塔在25 m/s左右出现的第一阶涡激振动,且在55 m/s风速左右又会出现一个明显的涡振区,这需要引起特别地注意。

图5 加设圆弧形导流板的气弹模型

图6 加设矩形垂直翼板的气弹模型
3 结论
通过风洞试验,以节段模型静力试验为主,气弹模型为辅进行结果验证的方式,研究了在建的某斜拉桥梁中倒角方形桥塔的驰振性能,并找出了对桥塔驰振安全性有改善作用的空气动力措施:加设圆弧形导流板可以将实际桥塔的最低驰振临界风速提升至70 m/s以上,而且发现圆弧形导流板同样可以有效抑制倒角方形桥塔的涡激振动;并证实了矩形垂直翼板同样可以有效提高实际桥塔驰振临界风速、改善驰振稳定性的观点,但却发现矩形垂直翼板对倒角方形桥塔的涡激振动无抑制作用。
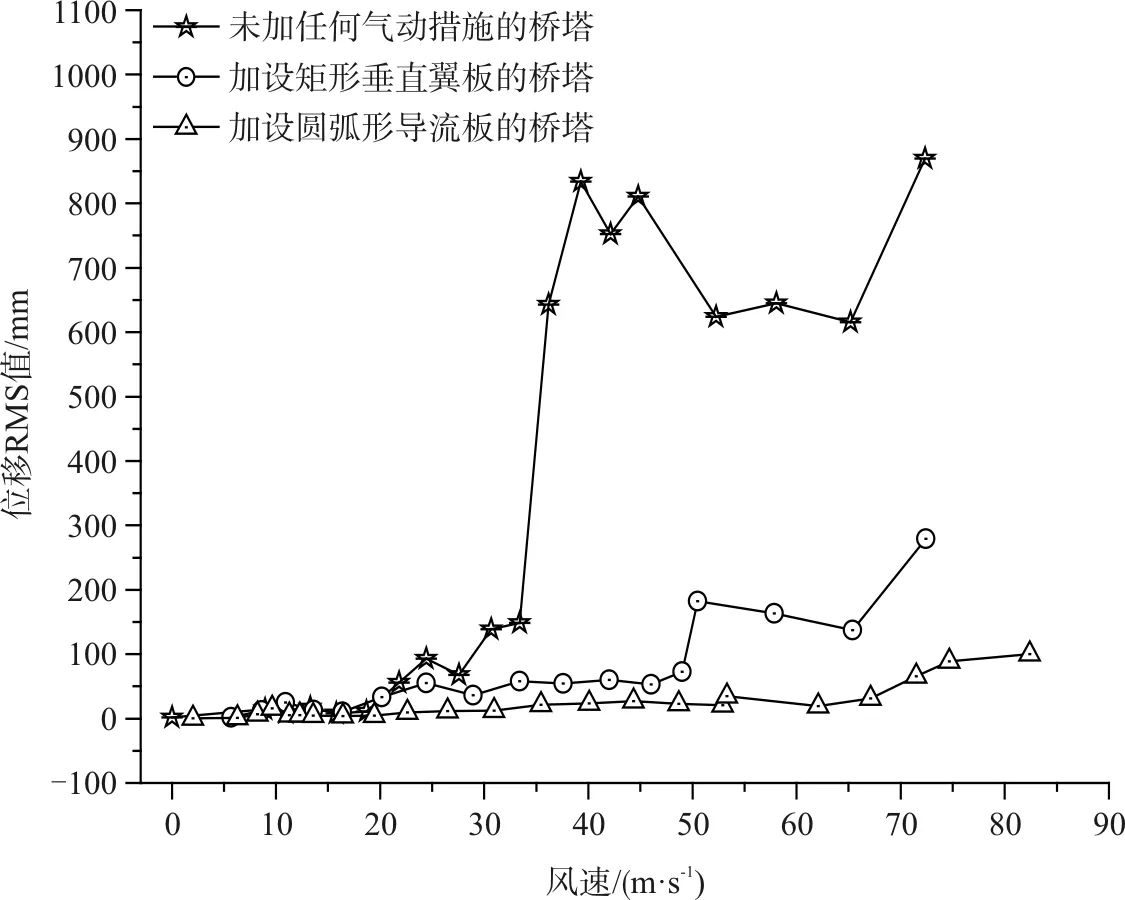
图7 加设气动措施后塔顶在0°风向角下的横风向位移均方根值

