基于多模态优化问题的粒子群算法研究

瞿博阳，谢 亮，李 超，刘凯松，乔百豪

(中原工学院 电子信息学院，河南 郑州 450007)

多模态优化(Multi-Modal Optimization，MMO)[1]问题是指包含多个全局或局部最优解的优化问题，如桁架结构优化、图像分割、电动汽车感应电机设计等都属于MMO问题。优化求解此类问题难度较高，要求算法在寻优过程中既要避免过早收敛(收敛于某个峰值点)，又要保证解的多样性(找到多个峰值点)。对于MMO问题而言，找到多个最优解具有许多好处：能为决策者提供更多有用的信息；有助于对问题中隐含的关系属性进行研究；能够为决策者提供更多可靠的选择；有助于提高算法求得全局最优解的概率。因此，提出一种能有效求解MMO问题的方法非常重要。

进化算法经常用于求解MMO问题，但存在求解过程复杂、效率不够高、多样性较差等不足之处[2]。粒子群算法(Particle Swarm Optimization，PSO)是由Kennedy J等提出的一种新兴的进化算法[3]。PSO算法的搜索原理来自对鸟类觅食行为的模仿，PSO算法中每个粒子以动态变化的速度在搜索空间中不断地搜索最优解，每个粒子在搜索空间中的位置坐标都代表待优化问题的“潜在可行解”。PSO算法结构简单，鲁棒性强，在工程实践领域有着十分广泛的应用[4-6]，具有很高的研究价值。针对MMO问题，本文研究了两种拓扑结构的PSO算法模型，在原算法的基础之上引入线性递减惯性权重进行改进，并使用15个多模态测试函数[7]对改进后的算法进行对比测试。

1 多模态优化问题

(1)

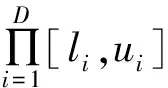
PSO算法中每个粒子包含两个动态变量：位置x(t)、速度v(t)。其中，x(t)表示候选解，x(t)∈X。通过PSO算法的不断优化，当种群中的某个粒子满足x(t)∈Xbest时，视为成功找到MMO问题的一个解。PSO算法的作用相当于一个“过滤器”，通过不断“筛选”，尽可能多地找到MMO问题的最优解Xbest(见图1)。

图1 PSO求解MMO问题

2 粒子群优化算法

PSO算法有许多不同的拓扑结构，主要有环型结构、星型结构、四群集型和冯·诺依曼型[8-9]4种，如图2所示。不同的拓扑结构决定了种群中粒子们共享信息的方式，同时还会影响算法的收敛速度和避免早熟的能力。

对于星型结构，每个粒子节点都处于连接状态，搜索信息在全局范围内共享，因此这种拓扑结构也被称作“全局拓扑(global topology)”或“全拓扑(all topology)”。对于环型结构，每个粒子个体与两个相邻的粒子相连接，仅仅与其左右两个邻居共享信息，因此粒子之间的平均距离非常大，形成了若干个局部搜索区。本文主要研究星型拓扑结构和环型拓扑结构的粒子群算法。

(a) 环型结构 (b) 星型结构 (c) 四群集型 (d) 冯·诺依曼型 图2 PSO算法的拓扑结构

2.1 星型拓扑结构粒子群算法

星型结构PSO算法的速度以及位置更新公式为：

vi(t+1)=wvi(t)+c1r1[pi-xi(t)]+c2r2[pg-xi(t)]

(2)

xi(t+1)=xi(t)+vi(t+1)

(3)

式中:vi(t+1)表示第i个粒子的当前速度；wvi(t)表示“速度部分”，代表历史速度对当前速度的影响；c1r1[pi-xi(t)]表示“认知部分”，代表粒子自身历史经验对当前速度的影响；c2r2[pg-xi(t)]表示“社会部分”，代表种群中其他粒子对当前粒子速度的影响；w表示惯性权重，取值小于1；c1和c2是两个加速常量；r1和r2是0到1范围内均匀分布的随机数；t表示当前迭代次数；pi表示第i个粒子所找到的历史最优解，即“个体最优”，pg表示种群中所找到的全局最优解，即“全局最优”；xi(t)和xi(t+1)分别表示第i个粒子的当前坐标位置以及下一时刻的坐标位置。

星型结构PSO算法的流程为：初始化种群，设定种群规模，随机生成对应数量的个体，根据式(1)中目标函数f(X)计算个体们的适应度值，更新个体最优和全局最优，随后根据式(2)、(3)更新粒子速度以及位置，循环迭代，直到找到所有最优解或达到评价次数为止(见图3)。

图3 星型结构PSO算法流程

2.2 环型拓扑结构粒子群算法

环型结构PSO算法的速度更新公式为：

vi(t+1)=wvi(t)+c1r1[pi-xi(t)]+c2r2[nbest,i-xi(t)]

(4)

环型结构PSO算法与星型结构PSO算法的不同点在于“社会部分”，c2r2[nbest,i-xi(t)]表示第i个粒子的“邻域最优”。nbest,i取pi-1、pi、pi+1中适应度值最高的一个。环型结构PSO的每个粒子通过左右相邻粒子的邻域最优与种群中其他粒子共享最优解的信息，如图4所示。图中，nbest,i=pi=nbest,i-1=nbest,i+1，依此类推。每3个相连的粒子相互形成一个小生境[10-12]，每个小生境中的粒子可能拥有同1个的邻域最优，也可能拥有3个不同的邻域最优，并朝着各自的领域最优移动。

图4 环型结构PSO的信息交流

环型结构PSO算法流程为：初始化种群，设定种群规模，随机生成对应数量的个体，根据式(1)中的目标函数f(X) 计算个体们的适应度值，更新个体最优和邻域最优，随后根据式(4)、(2)更新粒子速度以及位置，循环迭代，直到找到最优解或达到评价次数为止(见图5)。

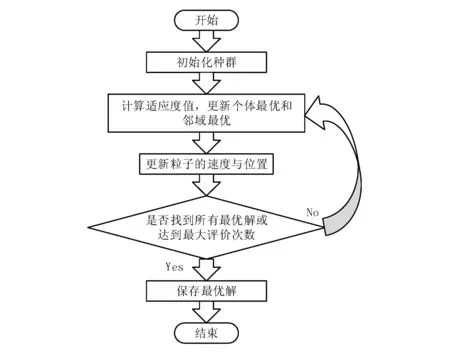
图5 环型结构PSO算法流程

2.3 线性递减惯性权重的引入

惯性权重w的大小从一定程度上决定了PSO算法的收敛速度以及搜索范围。当w的值比较大时，整个种群的全局搜索性能更强，而当w较小时，则更有利于粒子们进行局部搜索。算法刚开始搜索时，全局搜索更能增强算法跳出局部最优的能力，而随着搜索过程的不断进行，适当地减小w，加强局部搜索，可以提高解的精度。

为了使算法搜索的多样性以及精度得到提高，引入线性递减惯性权重，让w从wmax线性减小到wmin，具体计算公式为：

(5)

式中：wmax、wmin分别被设定为0.9、0.4；t为当前迭代次数；tmax为最大迭代次数。

3 评价方法

成功率(SR)和峰值比(PR)可用于评估算法求解MMO问题的能力。

SR是指成功找到所有最优解的次数NSR与总运行次数run的比例。计算成功率时，需要根据参数精确度ε和小生境半径radius来确定某一次运行是否成功找到最优解。当候选解对应的适应度值与实际最优值的误差在ε之内时，计算候选解与实际最优解的欧几里德距离，若所求得的距离差在radius以内，则视为成功找到了一次最优解。

PR按照公式(6)计算：

(6)

式中:run表示运行次数；NPFi表示每次运行所找到的最优解的个数；NPR表示运行run次后所找到的最优解的个数；NKP表示已知最优解的个数。PR值越大表示算法性能越好。

4 实验及结果分析

本文选取文献[7]中提出的15个复杂的测试函数对两种不同拓扑结构的PSO算法进行测试。表1中给出了这些多模态测试函数的相关属性。表中每个多模态测试函数包括3个不同的维度，每个维度下，测试函数所包含的最优解的数量也不同，因此，每种算法都需要对不同维度下的测试函数进行独立求解。

表1 测试函数简介表

表3给出了改进后两种PSO算法的成功率(对于二者求解成功率均为0的问题，表中未列出)。星型结构PSO算法求解5维f1时成功率为0.353，求解10维f1时成功率为0；环型结构PSO算法求解5维f1时成功率为0.627，求解10维f1时成功率为0.098；星型结构PSO算法求解2维f2时成功率为0，环型结构PSO算法求解2维f2时成功率为1。星型结构PSO算法求解5维f4时成功率为0.059，环型结构PSO算法求解5维f4时成功率为0.313。星型结构PSO算法求解6维f7时成功率为0，环型结构PSO算法求解6维f7时成功率为0.039。从实验结果可以看出，改进后的环型结构PSO算法成功率更高。

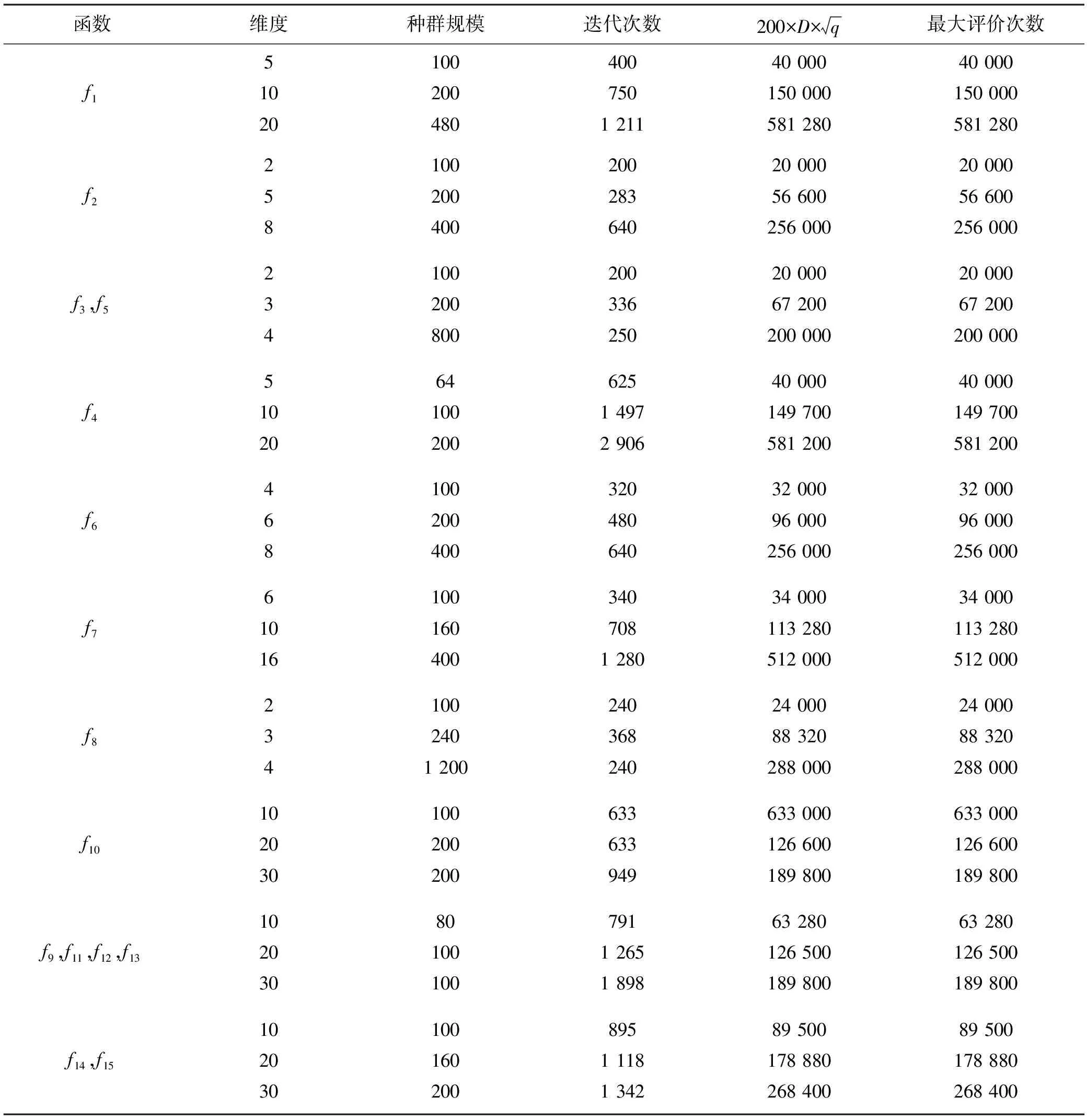
表2 参数设定表

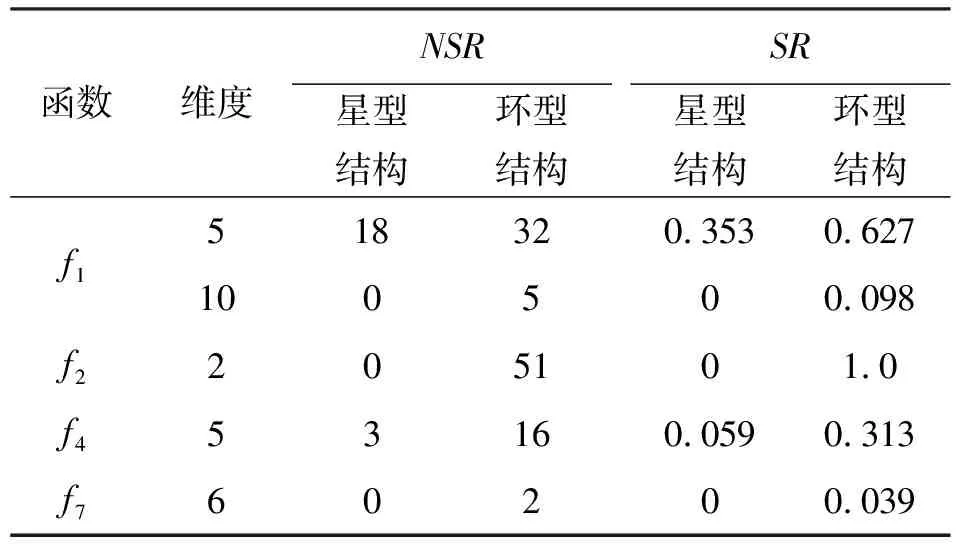
表3 两种PSO算法的成功率(SR)

表4给出了改进后两种PSO算法峰值比(对于二者均未成功找到最优解的问题，表中未列出)。对于5维f1，星型结构18次成功找到最优解，环型结构43次成功找到最优解，峰值比分别为0.353和0.843；对于10维f1，星型结构未能成功找到最优解，环型结构找到3次，峰值比分别为0和0.059。除去20维的f13，改进后环型结构PSO算法求解剩余测试函数的效果均远远优于改进后的星型结构PSO算法。

表4 两种PSO算法的峰值比(PR)

从表3和表4可以看出，通过成功率和峰值比的结果对比，改进后的环型结构PSO算法在求解MMO问题时，具有更高的精度和更好的搜索多样性。

5 结 语

针对传统算法在求解MMO问题时，存在求解过程复杂、多样性差等不足，提出用环型结构PSO算法和星型结构PSO算法求解MMO问题，并引入了线性递减惯性权重来提高算法的精度和多样性。通过仿真实验，改进后的环型结构PSO算法具有更强的全局搜索能力和局部搜索能力，能够避免陷入MMO问题的局部最优解，有着更好的稳定性，在求解MMO问题是有效和可行的。星型结构PSO算法则需要进一步提高其局部搜索能力。