基于粒子群的模糊神经网络养殖池塘溶氧预测研究

赵景波， 薛秉鑫

(青岛理工大学信息与控制工程学院，山东青岛 266520)

溶氧是水产养殖中的一项重要参考指标，对水产养殖的产量有重要影响。池塘溶氧受温度、光照、氨氮和浮游生物等多种因素影响，各影响因素之间存在复杂的相互关系，传统的经验估算无法准确判断溶氧量，错误判断会影响水产养殖的产量，造成经济损失。掌握水中溶氧变化情况、实现溶氧量的准确预测，对现代水产养殖具有十分重要的经济价值和现实意义。

目前，国内外学者提出一些对溶氧进行预测研究的方法。张垒等[1]建立基于小波神经网络的预测模型对天然水体溶氧进行预测研究；马从国等[2]研制了一种基于无线传感网的水产养殖池塘溶氧智能监控系统，实现对池塘溶氧的分布测量、智能控制和集中管理；Liu等[3]提出基于改进粒子群优化的最小二乘支持向量回归法，预测河蟹养殖中溶氧含量，并将预测结果与BP神经网络的预测结果进行对比；Emamgholizadeh等[4]建立人工神经网络和ANFIS模型对溶氧进行计算并得到了较好的试验结果；Heddam[5]提出基于去噪方法的自适应模糊神经网络对溶氧进行预测，并将其预测结果与多元线性回归模型进行比较分析；宦娟等[6]提出一种基于经验模态分解和自适应扰动粒子群优化最小二乘支持向量机的组合预测模型，提高了溶氧的预测精度和有效性。

本研究采用粒子群算法[7-11]优化的模糊神经网络[12-15]对溶氧进行预测，弥补了常规BP算法收敛速度慢、易陷入局部极值点的缺陷。采用池塘水体温度、氨氮、pH和亚硝酸盐氮作为模糊神经网络的输入变量，并采用小波包分析[16-18]对采集的信号进行消噪处理，神经网络的输出变量则是池塘溶氧。

1 溶氧影响因子确定和数据采集

1.1 溶氧影响因子确定

与溶氧量有关的因素有光照、风速、气压、水温、底泥耗氧、浮游动植物耗氧、化学耗氧以及注入新水和增氧机使用等。由于研究的是露天池塘，注入新水和增氧机使用都是人工调控。注入新水时溶氧增加较少，开增氧机的时间也基本固定，这些因素可以隐含在其他因素中，因此在输入项中省去这2个因素。由于条件限制，环境因素无法准确测量，所以选择在相似的晴朗天气下对数据进行采集，尽量避免由于天气变化对溶氧预测的干扰。在相关因素中，底泥和浮游动物的耗氧量较小，对溶氧量的影响很小，浮游植物在夜间呼吸耗氧量大，但无法对其进行检测，因此这3个因素也不予考虑。淡水池塘养殖中，化学耗氧量较高，对溶氧量影响较大，但其检测非常困难，因此本研究选择pH、氨氮和亚硝酸盐氮等3个可测因素来反映池塘的化学耗氧量，且这3个因素均在一定程度上会对溶氧量造成影响。

1.2 数据采集

试验选在青岛某水产养殖场，养殖场占地面积145 hm2，建有池塘循环水系统，配备增氧机、溶氧检测仪和水产养殖远程无线监控系统等渔业设备。研究数据来源于远程无线监控系统，该系统每2 h在线采集一次数据，选取2017年夏季相似的晴朗天气共33 d，获得数据396组。对数据进行筛选，保留数据375组。取360组数据对模糊神经网络进行训练，剩余的15组数据则用于对神经网络的性能进行检验。

2 小波包分析理论

小波包分析为信号处理提供了一种更加精细的分析方法，通过将频带进行多层次划分，可对小波分析没有细分的高频部分作进一步分解。小波包分析可根据分析信号特征，自适应地选择相应的频带，使之与信号频谱相匹配，从而提高时频分辨率。采用分解图的形式表明小波分解和小波包分解的区别，以3层分解为例，见图1、图2。

图中，S表示信号，A表示信号分解低频部分，D表示信号分解高频部分，序号1、2、3表示分解的层数。如A1表示信号第一层分解的低频部分，D1表示信号第一层分解的高频部分，接下来就是对已经分解的信号作进一步分解。

图1 信号的3层小波分解

图2 信号的3层小波包分解

(1)

(2)

3 基于粒子群算法优化的模糊神经网络

3.1 模糊神经网络模型

模糊神经网络是模糊集理论和神经网络相结合的产物，既有神经网络的大规模并行处理能力、自学习能力和自适应能力，又可以处理模糊信息，完成模糊推理功能，性能优越。该预测模型为多输入单输出的4层网络模型(图3)。这4层分别是输入层、模糊化层、模糊规则层和输出层。

图3 模糊神经网络结构

第一层为输入层，输入层神经元个数与输入变量个数相同，输入向量为x=(x1,x2,…,xn)T。y为输出层变量，由于输出变量只有一个，所以输出层只有一个神经元。系统的第j条模糊规则[12]可表示为：

Rj:如果x1=X1j,x2=X2j,…,xn=Xnj,那么y=Yj

(3)

式中：Rj—第j条模糊规则；xi—输入变量；Xij—输入变量所对应的模糊子集，i=1,2,…,n，j取决于每个输入变量的模糊子集数；y—输出变量；Yj—第j条规则的结果，j取决于模糊规则层神经元个数。

第二层为模糊化层，计算每个输入变量的隶属度。采用正态分布函数作为隶属度函数，第i个输入变量对模糊子集Xij的隶属度计算公式为：

(4)

式中：μXij(xi)—输入变量xi对模糊子集Xij的隶属度；xi—输入变量；mij—正态分布函数的期望；σij—正态分布函数的标准差，输入变量的隶属度完全由参数mij和σij决定。

第三层为模糊规则层，根据模糊理论定义模糊化层和模糊规则层的连接权值为：

μj=μX1j(x1)×μX2j(x2)×…×μXnj(xn)

(5)

式中：μj—模糊化层和模糊规则层之间的连接权值，j取决于模糊规则层神经元个数；μXij(xi)—输入变量xi对模糊子集Xij的隶属度，i=1,2,…,n，j取决于每个输入变量的模糊子集数；xi—输入变量；mij—正态分布函数的期望，σij—正态分布函数的标准差。

模糊神经网络第三层到第四层完成模糊决策功能，假设系统中有m条规则，本次设计使用加权平均法[12]进行去模糊化处理，得到输出为：

(6)

式中：y—输出变量；wj—模糊规则层与输出层之间的连接权值，j=1,2,…,m；μj—模糊化层和模糊规则层之间的连接权值。

对模糊神经网络进行训练，需要确定的参数为正态分布函数的期望mij和标准差σij以及连接权值wj。神经网络常用的算法为梯度下降法，该算法收敛速度慢，容易陷入局部最优化问题，难以得到全局最优解。为解决这一问题，本研究采用具有全局优化性能的粒子群算法对模糊神经网络的参数进行优化。

3.2 粒子群优化算法

3.2.1 粒子群算法的数学描述

如果在某个D维空间内寻找目标，种群由m个粒子构成。种群中每个粒子有它自己的位置，将第i个粒子的位置采用xi=(xi1,xi2,…,xiD),i=1,2,…,m表示，其速度也是一个D维向量，记为vi=(vi1,vi2,…,viD)。每个粒子在经过一个新的位置时，就与之前所经过的所有位置进行比较，当第i个粒子飞行到某一位置后，设它所经过的最优位置为pi=(pi1,pi2,…,piD)。而将粒子群中每个粒子所经过的最优位置进行比较，得到粒子群所经过的最优位置，并将它表示为pg=(pg1,pg2,…,pgD)。每个粒子按照下列公式[10]进行位置变化：

vid(t+1)=wvid(t)+c1r1[pid-xid(t)]+c2r2[pgd-xid(t)]

(7)

xid(t+1)=xid(t)+vid(t+1)

(8)

式中：i—粒子数，i=1,2,…,m；d—空间维数，d=1,2,…,D；t—时刻；w—惯性权重且为非负数；c1、c2—加速因子定义为常数；r1、r2—随机数且在0和1之间均匀分布；pid—粒子i最优位置；pgd—粒子群最优位置；xid(t)—粒子i在t时刻的位置，xid(t)∈[-xmax,xmax]；vid(t)—粒子i在t时刻的速度，vid(t)∈[-vmax,vmax]，xmax和vmax是非负数。

3.2.2 粒子群算法流程图

粒子群算法流程图如图4所示。随机初始化粒子的位置和速度，计算粒子适应度值，进行粒子位置与最优位置比较，并判断是否满足收敛准则。若满足，输出粒子位置作为粒子群最优位置；若不满足，更新粒子的位置和速度，迭代继续。

图4 粒子群算法流程图

3.2.3 适应度函数和参数优化步骤

用粒子群算法优化模糊神经网络的连接权值和隶属度函数，即设粒子群的位置向量xi的元素是模糊神经网络的连接权值、隶属度函数的期望和标准差。神经网络的训练主要是为了使网络中的参数误差最小，因此，适应度函数可以定义为：

(9)

式中：fit—适应度函数；Ns—训练集样本数；Yi—期望输出；yi—实际输出。

基于粒子群算法的参数优化步骤：1)初始化，随机初始化每个粒子的位置和速度，确定种群数目、惯性权重和加速因子等参数；2)计算每个初始粒子的适应度值，pi为当前粒子最优位置，pg为粒子群最优位置；3)根据公式(7)、(8)更新粒子的位置和速度，产生新的粒子；4)返回步骤2)，直到满足收敛准则，迭代停止，全局极值即为训练问题的最优解。

4 预测模型建立与仿真分析

4.1 预测模型建立

本研究提出基于小波包分析和粒子群算法优化模糊神经网络的组合预测模型，利用多相关因子预测溶氧量。模型输入变量为温度、亚硝酸盐、氨氮和pH，输出变量为池塘溶氧。预测流程如图5所示，建模步骤如下：

(1)小波包变换消噪处理。远程无线监控系统对数据进行采集，对采集的原始信号进行小波包变换，设置分解尺度为3，选择逼近信号并将数据分为训练数据和测试数据。

(2)模糊神经网络建立与训练。通过聚类算法[19-22]确定神经网络的结构，利用Kohonen网络对模糊隶属度个数进行选取，确定每个输入变量分为3个模糊子集，因此模糊神经网络的结构为4-12-81-1。随后利用训练数据对模糊神经网络进行训练。

(3)网络参数优化。初始化粒子群算法，设置种群数目为30，加速因子为c1=c2=2，适应度阈值为0.001，最大允许迭代次数为350。

(4)模型预测。利用测试数据对模型进行验证，得到最终预测结果。

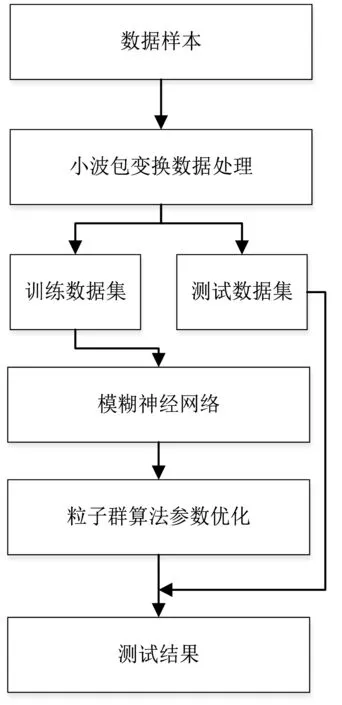
图5 预测流程图

4.2 仿真分析与讨论

4.2.1 小波包变换数据处理

远程无线监控系统对数据进行采集，以溶氧为例，获得溶氧原始信号(图6)。对该原始信号进行小波包分解，选择分解尺度为3。对其尺度系数和小波系数进行重构，得到逼近信号和细节信号，并利用逼近信号建立数据集。

4.2.2 仿真结果与讨论

构造两类模糊神经网络，一类采用梯度下降法训练神经网络参数(FNN)，另一类则采用粒子群算法(FNN-PSO)。试验数据经小波包变换进行消噪处理。两类模糊神经网络性能对比如图7所示,实测样本数据和模型预测值见表1。

表1所示测试结果表明，进行测试的15组数据中，FNN-PSO对溶氧的预测值和实测值之差在|Δ|<0.15 mg/L之内的为14组，占测试总样本数的93%，大于0.15 mg/L的仅有1组(第6组)，误差为0.17 mg/L。

选用均方根误差(RMSE)，平均相对误差均值(MAPE)和平均绝对误差(MAE)[6]对表1数据进行误差分析，得到误差指标(表2)。

图6 溶氧原始信号和小波包分解后的溶氧逼近信号、溶氧细节信号

(10)

(11)

(12)

由表2可知，试验数据经小波包变换处理后，预测溶氧值时，FNN-PSO与FNN相比，误差指标均方根误差(RMSE)、平均相对误差均值(MAPE)、平均绝对误差(MAE)分别降低了22.75、3.97、22.86个百分点。各项误差指标证明了粒子群算法的有效性，预测精度要高于常规的BP算法。根据图7可以直观地看出，基于小波包变换和粒子群算法优化模糊神经网络的组合预测模型对实测样本具有较好的拟合能力。

通过对比研究，进一步证明了小波包变换的有效性。选择FNN-PSO为预测模型，将试验数据分为两类：一类是经小波包变换进行消噪处理的数据，另一类则是未经处理的原始数据。对预测结果进行误差分析，得到误差指标(表3)。

图7 实测值、FNN和FNN-PSO性能对比图

序号温度/℃亚硝酸盐/(mg/L)氨氮/(mg/L)pH溶氧/(mg/L)FNN预测值/(mg/L)FNN-PSO预测值/(mg/L)120.10.0110.0787.26.186.536.30218.70.0350.0667.95.755.395.61318.10.0060.0458.45.165.545.29419.60.0380.0817.56.366.706.50517.50.0080.0616.85.255.625.36619.30.0240.0657.46.306.626.47719.10.0240.0888.05.555.165.45819.70.0080.0707.55.925.545.78918.90.0410.0667.85.806.125.911018.50.0250.1087.16.336.666.441117.80.0180.0586.65.154.785.081218.40.0280.0758.25.655.305.541318.50.0260.0857.75.825.465.701419.90.0360.0817.36.285.976.181519.40.0120.0777.66.016.326.15

表2 预测结果误差指标(1)

表3 预测结果误差指标(2)

由表3可知，在相同的预测模型条件下，预测溶氧值时，选用小波包变换处理的数据与原始数据相比，误差指标RMSE、MAPE、MAE分别降低了16.82、3.36、16.65个百分点。综合以上仿真结果，本研究提出的基于小波包变换和粒子群算法优化的模糊神经网络模型可对溶氧值进行有效预测，并具有较高的预测精度，在水产养殖溶氧调控方面具有一定的实际参考价值。

5 结论

基于小波包变换和粒子群算法优化模糊神经网络的组合预测模型具有较高的预测精度，可保证93%的预测值和实测值的误差小于0.15 mg/L。通过对养殖池塘溶氧的有效预测，可及时掌握溶氧变化情况，对水产养殖的调控与管理具有一定的实际参考价值。

□