分布式母线差动保护耐同步误差能力分析
陈 雷,高厚磊,樊占峰
1. 山东大学 电网智能化调度与控制教育部重点实验室,山东 济南 250061;2. 许继集团有限公司,河南 许昌 461000)
0 引言
智能变电站中分布式母线差动保护实现就地分散数字化采样[1-3],数据采样无法做到完全同步;而且对设有冗余配置,并采用“网采网跳”的母线差动保护,由于数据在网络上的传输延时不定,易出现数据不同步问题。目前母线差动保护同步方案主要有2类:一类是采用外设或内部同步时钟[4]实现分布式采样系统各单元间的数据同步,主要有基于全球定位系统(GPS)时钟和基于IEEE1588的网络对时方式[5-7];另一类是利用自同步技术实现数据同步[8-9]。GPS对时会出现失步和同步误差增大的情况;自同步技术也无法做到完全同步。母线差动保护判据本身具有相移制动能力,能够耐受一定的同步误差,但目前未见对其能耐受的同步误差角度的定量分析,也缺少对影响其耐受同步误差能力因素的分析。因此,母线差动保护的耐受同步误差的能力是亟待研究的问题。
目前鲜有母线差动保护耐同步误差能力的研究方法和成果。文献[10]分析了线路差动保护的相移制动能力,但该方法不适用于母线差动保护;文献[11]从采样不同步角度分析了同步误差对母线采样值差动保护的影响,但是缺少对保护判据耐同步误差能力的分析;文献[12]分析了数字化变电站中独立于GPS的同步时钟源的必要性,并比较了现有几种同步实现方案的特点,但是没有对各种同步方法可能产生的最大同步误差进行分析。不同于两端线路系统,母线属于多端系统,连接的电气设备复杂多样,且数量不定,差动电流和制动电流的计算要考虑多端单元,各单元之间数据的相对不同步方向存在差异。相比于线路差动保护,母线差动保护耐受同步误差能力的分析难度大。
本文针对智能变电站分布式母线差动保护的研究现状和需要解决的实际问题,以普通比率制动特性的双母线结构差动保护为例,提出了同步误差允许裕度角的概念;从被保护母线角度分析了不同步电流的幅值、数量和性质,数据不同步方向,电流互感器饱和以及母线连接结构对同步误差裕度角的影响,从保护判据角度分析了制动系数的影响;推导并定义了相移系数,以表征不同步角度对差动电流的影响程度,并理论推导得到了在单个影响因素以及综合影响因素下,母线差动保护能够耐受的最小同步误差允许裕度角。通过大量的仿真计算,验证了理论分析的准确性,并给出了快速有效确定母线差动保护最小同步误差允许裕度角的方法。
1 母线差动保护最小同步误差允许裕度角
数据不同步在相量中表现为相位角的偏移。为简化分析,先假设电流互感器无传变误差,工作于理想状态。
普通比率制动特性母线差动保护判据为:
(1)
其中,Ii为第i个单元电流相量;n为单元总数;K为制动系数;Iset.0为最小启动门槛。


图1 同步误差引起电流相量相移示意图Fig.1 Schematic diagram of current phase shift caused by synchronization error
2 β值影响因素分析
2.1 不同步单元电流幅值的影响

(2)
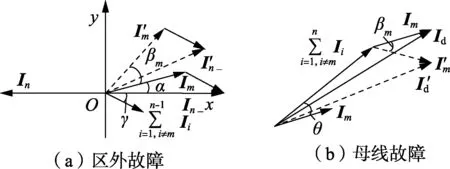
图2 相移分析示意图Fig.2 Schematic diagram of phase shift analysis

(3)
联合式(2)和(3)可得:
Id=Kd|Im|
(4)

定义相移系数Kd表征β对Id大小的影响程度。
根据式(1),构造函数:
f=Id-KIr
(5)

母线差动保护不正确动作的边界条件为f=0,将Id和Ir代入式(5)可得:
βm=2 arcsin[K(1+m1)/(2m1)]
(6)

β随m1变化的曲线如图3所示。由图可见,β随着m1的增大而减小,且受其影响变化先快后慢。分析可知,m1的取值范围为(0,1]。当m1取极端值m1=1,且K=0.25时,由式(6)可得此时的最小同步误差允许裕度角β≈28.9°。
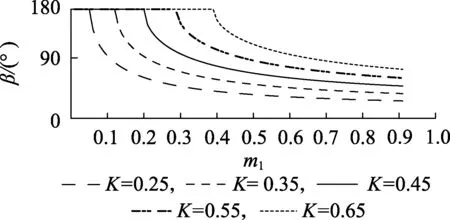
图3 β随m1变化关系曲线Fig.3 Curves of relationship between β and m1
2.2 不同步单元数量和电流性质的影响
发生母线差动保护区外故障时,不同步单元数量的影响要视电流性质分2种情况讨论:一是所有不同步单元电流均流入母线(情况1);二是部分不同步单元的电流流入母线、部分不同步单元的电流流出母线(情况2)。
a. 情况1。
假定有h(1≤h≤n-1)个不同步单元的电流流入母线,分析可得:
(7)
为简化分析,可令h个不同步单元电流初始相位相同,即满足α1=α2=…=αh=0°,则由式(7)可得:
(8)
若相移β1=β2=…=βh=β且相移方向一致,代入式(8)可得:

(9)
因各单元电流幅值不变,所以制动电流Ir大小不变。将Id、Ir代入式(5),令f=0,可得:
(10)

b. 情况2。
假定有h(0≤h≤n-1)个不同步单元电流流入母线,流出母线不同步单元电流为In。同情况1的分析,可得:
(11)
令β1=β2=…=βh=βn=β且不同步方向一致,代入式(11)可得:

(12)
将Id、Ir代入式(5),并令f=0,可得:
(13)
由式(13)可知,β与h呈正相关。即当不同步单元电流包含流出单元电流In时,流入单元不同步数量h越多,β值越大,母线差动保护可耐受更大的不同步角度,与情况1中的结论相反。
当取极端值h=0时,有Ir/|In|=2,取K=0.25,由式(13)计算可得极端情况下最小同步误差允许裕度角β≈28.9°。
2.3 不同步方向的影响
在2.2节中,假定所有不同步单元的相移方向一致。若h个不同步单元中有q(0≤q≤h)个不同步单元的相移方向与之相反,并假设所有不同步单元相移角为β、电流幅值为|I|,则2.2节中的情况1经求解可得:
(14)
其中,Kq1=4q(q-h)。
当q=0或q=h时,结论与2.2节情况1分析一致。当0 对2.2节中的情况2,经求解可得: (15) 其中,Kq2=2q|I|/(|In|-h|I|)。 由式(5)、(15)可知,当0 2.2、2.3节所得结论对不同步单元的电流幅值不相等和相移角度大小不一致的情况同样成立。 发生区外故障时,由式(6)可得β、K的关系为: (16) β随K变化的曲线如图4中实线所示。可见,发生区外故障时,β与K呈正相关。当Im为故障线路单元电流时,有最小值Ir/|Im|=2,取K=0.25,由式(16)计算可得最小同步误差允许裕度角β≈28.9°。 发生母线故障时(见图2(b)),β与K的关系为: (17) β随K变化的曲线呈图4中虚线所示。由图可见,发生母线故障时,β与K呈负相关。当取最小值Ir/|Im|=2,且K=0.7时,由式(17)计算可得最小同步误差允许裕度角β≈91.1°。 图4 β随K变化的曲线Fig.4 Curves of β vs. K 对于单母线、单母分段、双母线、双母线单分段、双母线双分段等母线结构,当采用式(1)所示判据的母线差动保护时,母线差动保护仅受与该段母线相连的线路单元、变压器单元、母联断路器单元以及分段断路器单元电流的影响,而与母线结构无关。 采用3/2断路器接线方式的母线,它的保护相当于2组单母线保护,发生母线故障时可能会有部分故障电流流出母线。由2.4节可知,发生母线故障时,差动保护具有很强的抗拒动能力,能承受约91°的不同步角,远大于发生区外故障时所能承受的不同步角28.9°,且流出的故障电流只会降低制动特性原理的母线差动保护的灵敏度,不会引起保护误动作。因此,母线差动保护耐同步误差能力与母线结构无关。 电流互感器饱和一般发生在电流幅值较大的故障线路单元中,饱和使得电流幅值减小,相位超前。 (18) 图5 线路发生故障时电流互感器饱和影响分析Fig.5 Effect analysis of CT saturation when fault occurs on transmission line a. 饱和单元的同步误差允许裕度角分析。 当r=1时,Id=Kd|In|,同2.1节分析可知,引起保护误动作的临界φ值即为最小同步误差允许裕度角。 当r≠1时,因不能确定r和cosφ的变化规律以及两者之间关系,只作定性分析:随着饱和程度的增大,r的减小会使得差动电流幅值急剧增大、制动电流幅值减小,导致很小的饱和单元不同步角就能引起母线差动保护误动作,从而降低了因采样不同步、网路数据设备等各处理环节产生的同步误差允许裕度角。 b. 非饱和单元的同步误差裕度角分析。 根据2.2节的分析可知,故障单元饱和导致相位超前,会增大非故障单元超前的同步误差允许裕度角,降低滞后的同步误差允许裕度角。 现有的母线保护装置均安装防止电流互感器饱和误动作措施,在发生母线区外故障且电流互感器饱和时能可靠闭锁,同时在发生区外故障转换为区内故障时,能保证母线差动保护快速开放、正确动作。所以母线差动保护耐受同步误差能力可以忽略电流互感器饱和的影响。 根据2.1—2.6节进行的分析,不考虑母线结构和电流互感器饱和,对各影响因素进行综合分析。 a. 考虑电流幅值影响的极端条件,即式(6)中m1=1时,可得: β=2 arcsinK (19) b. 考虑不同步单元数量和电流性质的影响时,2.2节中情况1的极端条件是h=n-1,情况2的极端条件是h=0,此时式(10)和式(13)均可转变为式(19)。 c. 考虑K值影响时,极端条件为Ir/|Im|=2,此时式(16)亦可转化为式(19)。当K取最小值K=0.25时,计算得β≈28.9°,受智能变电站采样频率4 kHz 限制,可得分布式母线差动保护能耐受6个采样点的不同步角度,即最小同步误差允许裕度角为: β=27° (20) 综上所述,在各影响因素取极端值时,均有式(19)所示形式。仔细分析可以发现,当某一因素取极端值的同时,其他各因素也相应取极端值,才可得到式(19),所以β=27°是考虑各种因素最不利条件下的综合分析结果。 利用PSCAD搭建如图6所示的220 kV双母线模型进行仿真分析,采用智能变电站4 kHz采样频率。 图6 220 kV双母线仿真模型Fig.6 Simulation model of 220 kV system with double-bus a. 电源参数:ZG1=ZG2=4.61+j52.70 Ω,ZG3=5.07 +j52.65 Ω,EG1=230∠20° kV,EG2=230∠25° kV,EG3=230∠10° kV。 b. 线路参数:L1、L2、L3线路长度分别为37、45、67 km,r1=0.035 76 Ω/km,l1=1.616 mH/km,c1=0.010 4 μF/km,r0=0.363 Ω/km,l0=4.211 mH/km,c0=0.007 39 μF/km。 c. 变压器参数:U1N/U2N/U3N=220 kV/100 kV/35 kV,SN1=SN2=100 MV·A。 在图6所示结构的基础上,各连接单元参数不变,只改变母线结构,搭建如图7所示的双母线单分段和单母线结构仿真模型。 图7 双母线单分段结构和单母线结构Fig.7 Structures of double bus single segment connection mode and single bus mode 本文除进行K对β的影响分析时K取不同值,其他情况下K=0.25。当线路L3发生AB两相接地故障时,表1给出了2种结构下各段母线分差动保护的βi值,表2给出了3种结构下母线总差动保护的βi值。由表1和表2可知,母线结构对β值没有影响。 表1 不同结构下各段母线分差动保护的βi值Table 1 Value of βi of each bus under different structures 注:Ⅰ、Ⅱ、Ⅲ分别表示相应结构下求得βi值的母线段。 表2 不同结构下母线总差动保护的βi值Table 2 Value of βi of whole bus differential protection under different structures 流出单元TA3电流幅值大于流入单元TA1,对比表1中TA1和TA3对应的β值可知,对于不同单元,电流幅值越大,对应的同步误差允许裕度角越小。 同一单元电流幅值大小的影响如图8所示,由图8可见,随着TA1一次电流幅值的增大,该单元的同步误差允许裕度角逐渐减小。 图8 TA1单元β值与电流幅值的关系Fig.8 Relationship between β and current amplitude of TA1 不同步单元数量的增多,可等效为一个单元电流幅值的增大。根据表3分析可知,不同步单元幅值的大小对β值的影响满足图3所示曲线关系:幅值增大,β值骤减,之后变化平缓。 表3 不同步单元不包含流出单元时不同步单元数量对β的影响Table 3 Influence of number of asynchronous units excluding diffluent unit on β 注:TA12表示TA1和TA2,其他类似。 图9 单母线多连接单元结构Fig.9 Structure of single bus with multi-connection units 由3.1节可知,β与母线结构无关,采用图9所示的多单元单母线结构分析β与不同步单元的电流性质、数量和方向的关系,以线路L3出口发生AB两相接地故障为例,对2种情况进行分析。 a. 当不同步单元不包含故障线路L3,且相移方向一致时,β与不同步单元数量的关系如表3所示。 图10为不同步角从0°变化到180°时,含有不同单元的Id-Ir曲线。各曲线与直线KIr的交点对应的角度即为β,显然,不同步单元数量越多,β越小,与表3共同验证了2.2节对情况1的分析是正确的。 图10 不同步角从0°变化到180°时不同步单元数量对应的差动特性Fig.10 Differential characteristics corresponding to asynchronous unit number when asynchronous angle changes from 0° to 180° 使所有流入单元不同步,并改变某些单元的不同步方向,得到的β值如表4所示。 表4 流入电流单元反方向不同步时不同步单元数量对β的影响Table 4 Influence of asynchronous number on β when direction of asynchronous influent unit is opposite 注:下划线表示对应单元的不同步方向与表3相反,后同。 表4表明,当不同步单元不包含故障线路时,β会随着反方向的不同步单元数量的增加先增大后减小,与2.3节的分析完全一致。 b. 当不同步单元包含故障线路L3,且各单元相移方向一致时,β与不同步单元数量的关系如表5所示。 表5 不同步单元包含流出单元时不同步单元数量对β的影响Table 5 Influence of asynchronous unit number on βwhen asynchronous units include diffluent unit 注:“—”表示β超出180°,后同。 由表5分析可知,当电流流出的故障线路单元L3不同步时,流入的不同步单元越多,β越大,母线差动保护的耐同步误差能力越强,与2.2节对情况2的分析结论一致。 保持TA3的不同步方向不变,逐渐改变其他各单元的不同步方向。此时,TA3与相反方向不同步单元的不同步角之和即为β。流出单元不同步时,反方向流入不同步单元数量对β的影响见表6,随着反方向不同步单元数量的增加,同步误差允许裕度角减小,验证了2.2节和2.3节理论分析的正确性。 表6 流出单元不同步时流入单元反方向不同步数量对β的影响Table 6 Influence of number of opposite direction asynchronous influent units on β when diffluent unit is also asynchronous 基于图6,设置母线Ⅰ发生AB两相接地故障,K值变化范围为0.3~0.7,母联单元TA4不同步,母线Ⅰ和母线Ⅱ故障相不正确动作的临界角度如表7所示。 表7 母线故障时K值对β的影响Table 7 Influence of K on β when bus breaks down 设置线路L3发生AB两相接地故障,使TA4单元不同步,得到母线保护不正确动作临界角度如表8所示。 表7和表8中母线和线路故障时母线Ⅰ的A相不正确动作角度随K变化的情况与图4完全相符,从而验证了2.4节分析的准确性。 从2.4节分析可知,发生母线故障时,在极端不利情况下,保护仍有很强的抗拒动能力,因此β值由线路故障时决定。由2.1—2.7节分析可知,决定β值的极端条件,可等效为电流幅值最大的故障线路单元发生不同步。对双母线以及分段母线结构,当1条或1段母线故障时,该故障对于非故障母线段属于外部故障,且一般情况下,母联单元或者分段单元电流幅值最大,所以β值由非故障母线差动保护决定,可由表7仿真结果验证。当线路故障时,与故障线路直接相连的母线分差动保护,其β值取决于故障线路单元不同步;与故障线路非直接相连的母线分差动保护,其β值取决于电流幅值较大的母联单元或者分段单元不同步,表1、表8结果可验证该结论。 表8 线路故障时K值对β的影响Table 8 Influence of K on β when transmission line breaks down 为正确评估分布式母线差动保护耐同步误差能力,本文提出了最小同步误差允许裕度角的概念。在对影响最小同步误差允许裕度角的各种因素进行全面分析的基础上,得到了该裕度角的理论值;同时通过建立220 kV双母线结构仿真模型,验证了本文分析结果的正确性。最小同步误差允许裕度角可用于判断因采样不同步、互感器传变特性以及网络数据设备等各数据处理环节产生的同步误差是否在保护正确动作的允许误差范围之内,亦可检验各种同步方案,尤其是采用自同步方法的母线差动保护能否达到同步要求。 对采用总差动和各段母线分差动保护方式的双母线以及母线分段等结构,本文给出了快速确定保护耐同步误差角度的方案,为母线保护设计人员及现场运行人员提供实用性参考。2.4 制动系数K的影响

2.5 母线结构的影响
2.6 电流互感器饱和的影响



2.7 各影响因素的综合分析
3 仿真验证

3.1 母线结构的影响



3.2 不同步电流幅值大小的影响


3.3 不同步单元的电流性质、数量和方向的影响

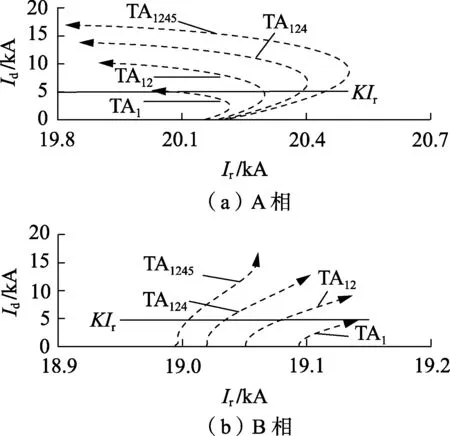
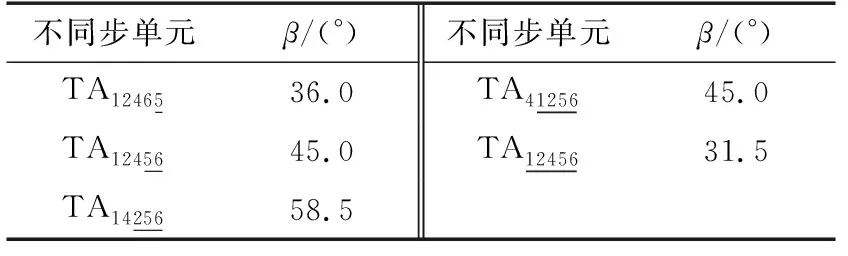


3.4 制动系数K值的影响


4 结论

