考虑电动汽车随机特性的机组组合问题研究

葛晓琳,裴晨皓

上海电力大学 电气工程学院，上海 200090)

0 引言

电动汽车EV(Electric Vehicle)在节能减排、遏制气候变暖以及保障石油供应方面有着无法比拟的优势，近年来得到了迅猛发展，产销量呈规模化增长[1]。然而，电动汽车的行驶特性具有不确定因素，当大规模电动汽车接入电网后，若不加以引导与控制，将会使得电网原有负荷“峰上加峰”，造成峰谷差加大，对机组组合问题产生影响[2]。为了减少电动汽车接入对电网的不利影响，充分利用电动汽车的储能特性，含电动汽车的机组组合问题得到了广泛关注。

文献[3]在机组组合模型的基础上，提出电动汽车最优充电模型，通过优化各调度时段的边际发电成本，合理分配电动汽车的充电时间段，但文中没有考虑电动汽车的反向放电能力。文献[4-5]则通过电动汽车入网V2G(Vehicle to Grid)技术将电动汽车充放电功率均作为优化变量引入机组组合模型中，在优化机组出力的同时优化电动汽车的充放电计划，以此作为电动汽车调度的优化方案。文献[6]分析了不同充电控制策略对机组组合优化结果的影响，并通过电动汽车放电增加系统的备用容量，提高电网运行可靠性。然而，上述文献只是对电动汽车进行简单的直接调度，即电网在任意时刻都能对电动汽车进行充放电控制。事实上电动汽车作为一种交通工具，其出行具有一定的随机性，因此充放电时段会受到限制。

文献[7-8]基于电动汽车出行的随机性，研究了电动汽车作为充电负荷的特性。文献[9-10]在考虑电动汽车随机接入的基础上，提出智能充电策略。文献[11]在机组组合问题中考虑了电动汽车的出行随机性，将电动汽车的充电需求纳入约束条件，并分析了不同的充电策略对机组组合优化结果的影响。文献[12]将私家车的随机出行特性融入电网调度的建模中，通过优化电动汽车的充放电功率减少了系统成本。但上述文献普遍以单一类型车辆的出行特征为蓝本，事实上电动汽车的类型不同，其出行的特征也不同[13-14]，在机组组合问题中如何考虑多种类型电动汽车的随机特性仍需进一步研究。

为此，本文在研究多类型电动汽车随机特性的基础上，建立了含电动汽车的随机机组组合模型。该模型将电动汽车分为私家车、公交车、公务车以及出租车4类，先研究各类型电动汽车的出行特性，然后随机模拟大量场景作为电动汽车的行驶数据，将其并入电动汽车的出行约束中，以此研究电动汽车的随机特性，通过对电动汽车充放电功率和机组启停的总体优化，降低了系统运行成本。最后基于10机系统的仿真验证了考虑电动汽车随机特性的重要性以及对不同种类电动汽车进行分类建模的必要性。

1 车辆出行随机特性分析

车辆的出行随机特性主要指用户出行具有随机性，包括车辆的离开时间、车辆的接入时间以及车辆的日行驶里程，这些因素会影响车辆在实际中参与调度的情况。通过对各类型电动汽车行驶特性的研究，包括私家车、公交车、公务车以及出租车4类，分析处理可得这4类车行驶数据并用于计算。

a. 私家车用户行驶特性。

对于私家车用户，可由2009年美国交通部对全美家用车辆的调查结果NHTS(National Household Travel Survey)的统计数据进行仿真模拟，分析处理得出车辆初始离开时间、车辆初始接入时间以及车辆的日行驶里程的概率密度函数[15]。其中车辆的接入时间与离开时间都满足正态分布，而车辆的日行驶里程满足对数正态分布。

b. 公交车用户行驶特性。

c. 出租车的行驶特性。

出租车作为一种营业型车辆，应保证其运营的效率最大化，充完电马上进行载客。为保证其运营的效率，出租车只参与充电而不参与放电[13]。而且，当出租车接入充电时马上使用快速充电，充电时间一般为0.5～1 h，之后马上投入运营。车辆的开始充电时间满足均匀分布，日行驶里程满足对数正态分布。

d. 公务车的行驶特性。

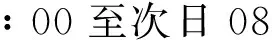
2 含电动汽车的随机机组组合模型

2.1 目标函数

含电动汽车的机组组合模型是在满足系统电力电量需求的前提下，按照节能、经济的原则对电动汽车的充放电进行合理的调度，使系统总成本最小，其目标函数如下：

CU(i,t)+CD(i,t)]}

(1)

火电机组的运行成本为：

CG(c,i,t)=u(i,t)[ai+biP(c,i,t)+ciP2(c,i,t)]

(2)

其中，u(i,t)为机组i在时段t的运行状态变量，u(i,t)=0表示机组i停机，u(i,t)=1表示机组i运行；ai、bi、ci为发电机组i的成本系数;P(c,i,t)为场景c时段t下火电机组i的功率。

火电机组的启动成本为：

(3)

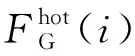
火电机组的停机成本为：

(4)

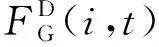
2.2 约束条件

2.2.1 火电机组约束

对于火电机组，有以下约束条件。

a. 负荷平衡约束：

(5)

其中，V为场景c下时段t所有电动汽车的类型(分别为私家车、公交车、出租车与公务车)；Pch(c,v,t)为场景c下所有v类车在时段t的充电功率；Pdis(c,v,t)为场景c下所有v类车在时段t的放电功率；D(t) 为时段t的系统负荷。

b. 系统备用需求。

上备用约束：

(6)

下备用约束：

(7)

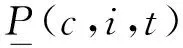
c. 机组出力约束：

(8)

d. 火电机组爬坡限制约束。

火电机组的爬坡约束分为机组的启动爬坡约束、机组的停机爬坡约束和机组在连续运行时段的爬坡约束。

机组的启停爬坡约束：

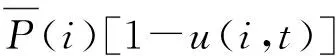
(9)

(10)

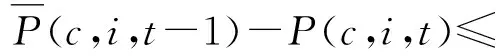
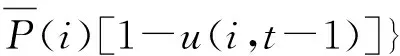
(11)

其中，SU(i)为机组i启动爬坡限制；SD(i)为机组i停机爬坡限制。

机组连续运行爬坡约束：

P(c,i,t-1)-P(c,i,t)≤RU(i)u(i,t-1)

(12)

P(c,i,t)-P(c,i,t-1)≤RD(i)u(i,t)

(13)

(14)

其中，RU(i)为机组i上爬坡约束；RD(i)为机组i下爬坡约束。

e. 火电机组最小启停约束：

[u(i,t-1)-u(i,t)][M(i,t-1)-TU(i)]≥0

(15)

[u(i,t)-u(i,t-1)][-M(i,t-1)-TD(i)]≥0

(16)

其中，TU(i)为机组i最小连续停机时间；TD(i)为机组i最小连续启动时间；M(i,t)为机组i在时段t已连续运行(正值)或连续停机(负值)的时间。

2.2.2 电动汽车相关约束

电动汽车作为交通工具，具有特殊的出行规律，这些出行规律具有的随机特性致使电动汽车的充放电调度具有随机性。在这些出行规律中，行驶起始时间以及行驶结束时间决定了可行的充放电区间，日行驶里程决定了用户的电量需求，电动汽车应该在满足这些条件下进行调度安排。

a. 出行时段约束。

当tin≤tout时，电动汽车只在[tin,tout]区间进行充放电：

(17)

其中，tin(c,v)为场景c下v类车单辆车的入网时段；tout(c,v)为场景c下v类车单辆车离网时段；X(c,v,t)为场景c下v类车单辆车在时段t的充电状态，X(c,v,t)=0表示车辆处于不充电状态，X(c,v,t)=1表示车辆处于充电状态；Y(c,v,t)为场景c下v类车单辆车在时段t的放电状态，Y(c,v,t)=0表示车辆处于不放电状态，Y(c,v,t)=1表示车辆处于放电状态。

当tout≤tin，电动汽车只在[1,tin]∪[tout,24]区间进行充放电：

(18)

b. 电动汽车充放电功率：

Pch(c,v,t)=Nev(c,v)PVch(c,v,t)

(19)

Pdis(c,v,t)=Nev(c,v)PVdis(c,v,t)

(20)

其中，Nev(c,v)为场景c下并入电网的v类车车辆总数；PVch(c,v,t)为场景c下v类车在时段t每辆车的充电功率；PVdis(c,v,t)为场景c下v类车在时段t每辆车的放电功率。由于各电动汽车的充放电行为缺乏同步性，为了规模化电动汽车用户充放电行为，用Pch(c,v,t)和Pdis(c,v,t)表示规模化电动汽车的充放电功率，其行驶起始时间、行驶结束时间以及日行驶里程都对应着相应的单辆电动车的行驶特征，是随机变量。

c. 电量平衡约束。

当电动汽车开始接入电网时，即t=tin(c,v)时，有：

SOC(c,v,t)=SOC0(c,v,t)

(21)

(22)

其中，SOC(c,v,t)为场景c下v类车单辆车在时段t的电池荷电状态；SOC0(c,v,t)为场景c下v类车单辆车在t=tin(c,v)时段初始电池荷电状态；SOCE(c,v)为场景c下v类车单辆车用户在离网时的电池荷电状态期望值；d(c,v)为场景c下v类车单辆车用户的日行驶里程；M(v)为v类车的百千米耗电量；Q(v)为v类车单辆车的最大电池容量。

当电动汽车在与电网连接时间段时，满足电动汽车的电量平衡：

Q(v)SOC(c,v,t)=Q(v)SOC(c,v,t-1)+

(23)

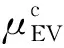
当电动汽车离开电网，即t=tout(c,v)时，车辆的电池状态必须满足用户的电池荷电状态期望值，因此有：

SOC(c,v,t)≥SOCE(c,v)

(24)

d. 电动汽车的充放电功率限制：

(25)

(26)

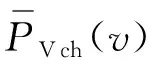
e. 电动汽车电池电量状态限制。

电动汽车要在保证不损耗电池正常寿命情况下进行充放电：

(27)

f. 电池充电限制。

车辆的充电量应保证不超过电池当前的可充电范围：

(28)

g. 电池放电限制。

车辆的放电量应保证不超过电池当前的可放电范围：

(29)

h. 电池可放电深度约束。

为了使电池损耗最小，当车辆处于放电状态时，需要对车辆的电池可放电深度进行约束：

DoD(c,v,t)=SOC(c,v,t)-SOC(c,v,t-1)

(30)

(31)

2.3 含电动汽车的随机机组组合模型求解

为了研究电动汽车随机特性，需要充分反映各类型电动汽车的出行特征。本文通过分析各类型电动汽车的出行数据得出各类型电动汽车的出行时间以及日行驶里程的概率密度函数。在此基础上，运用拉丁超立方抽样，通过对抽样概率分布进行分层，再从各间隔或各层次随机抽样[16]，得到大量场景来模拟各类电动汽车接入时段tin、车辆离开时段tout以及车辆日行驶里程d。同时为了平衡求解精度和难度，基于同步回代技术的场景减缩法[17]，消除部分出现概率较小的场景并将概率合并到相近的场景，形成缩减的预测场景，作为机组组合的场景输入。

此外，针对所建立的考虑电动汽车随机特性的机组组合模型，考虑到该模型属于多变量、多时段、非线性的动态最优化问题，采用文献[18]中的线性化方法将随机机组组合中的非线性约束转换为混合整数线性规划MILP(Mixed Integer Linear Programming)模型进行求解。最后将转换后的模型在GAMS平台上仿真实现，并采用商用的CPLEX软件包进行求解。

具体的流程图如图1所示。

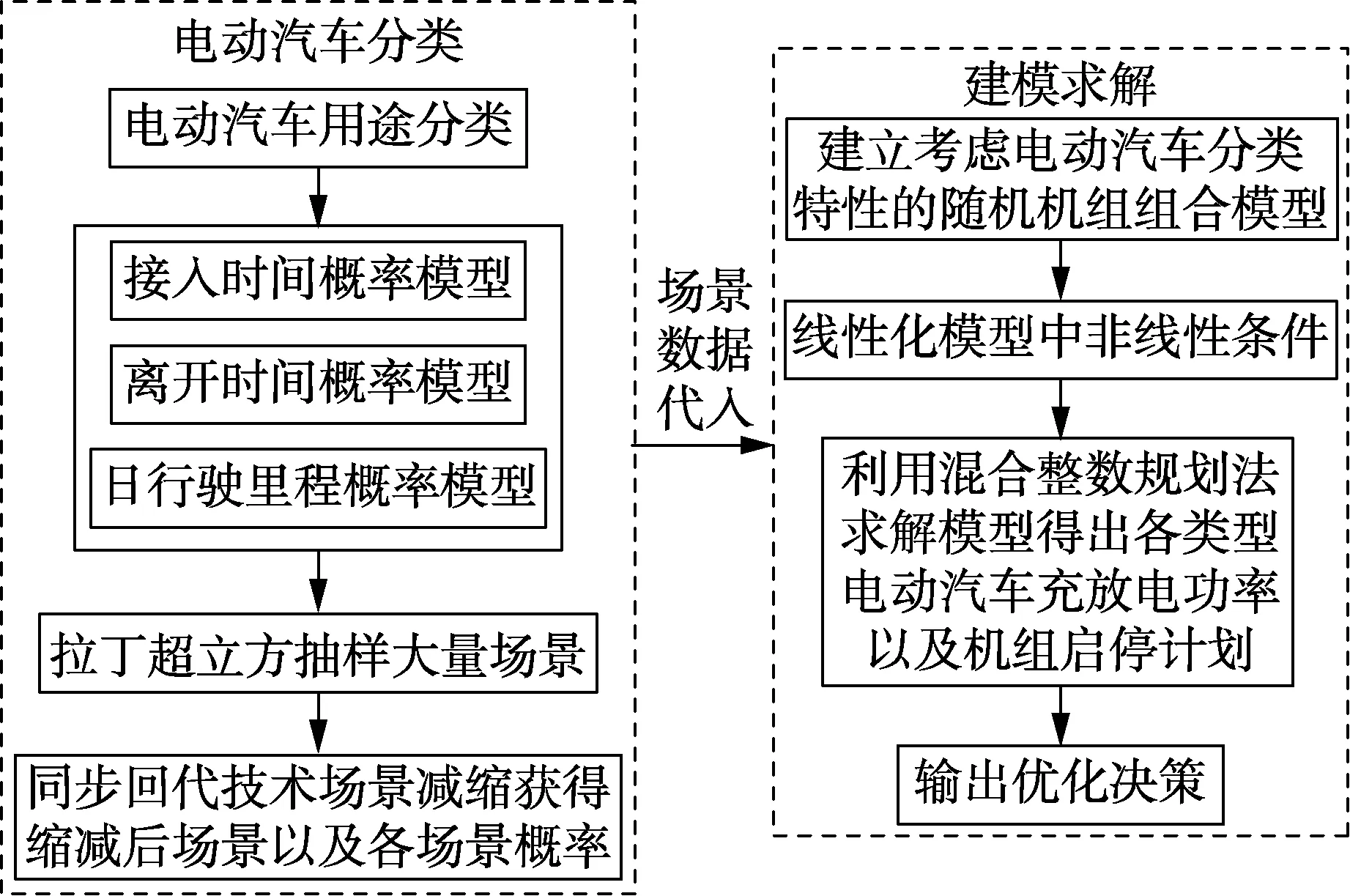
图1 模型求解的基本流程图Fig.1 Basic flowchart for solving model

3 算例分析

3.1 算例数据

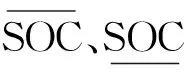
利用场景减缩法对各类电动汽车的出行行为进行合理分析，并在运用相应的抽样方法抽取10 000个样本的基础上，利用同步回代技术进行缩减运算，缩减后样本个数为100。与原始的10 000个场景的优化结果进行对比，如表1所示，从表中可以看出缩减后与原始场景的误差相差很小，优化结果误差在1%以内，且运算时间大幅缩短。因此，接下来将采用缩减为100个场景时的数据进行计算。

表1 缩减前后结果对比Table 1 Result comparison between before and after reduction

3.2 电动汽车随机特性的研究

考虑电动汽车的随机特性即需要考虑电动汽车的随机出行特性。以私家车为例，图2显示私家车日行驶里程的概率分布图，车辆的日行驶里程决定了车辆开始充电时的荷电状态。图3显示车辆的离开时间与车辆的接入时间的概率分布，电动汽车的可调度时间范围会遵循其出行规律，而不是24 h完全控制车辆的充放电行为。图4显示当车辆考虑随机特性与不考虑随机特性时各时段的充电功率对比。当考虑电动汽车随机特性时，车辆的出行时间以及充电需求都满足一定的随机性，电动汽车的可充电时间区间会在满足车辆的随机特性下安排；而不考虑车辆的随机特性时，电动汽车的充电安排集中为机组组合服务，车辆只需安排在一天内的几个时段完成充电，使得机组组合最优即可。因此，考虑电动汽车的行驶特性时，充电的功率分布在各个时段都有出现，不考虑车辆的随机特性时，电动汽车集中在一天内的几个时段进行充放电安排，两者会产生较大区别。以上分析表明，在对电动汽车进行充电安排时，需要考虑电动汽车的随机特性，否则得到的优化策略会与实际应用产生一定的差异。

图2 电动汽车日行驶里程数概率分布Fig.2 Probability distribution of travelled mileage of EV

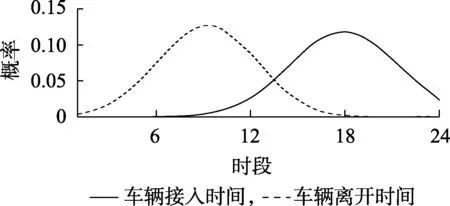
图3 电动汽车离开时间与接入时间概率分布Fig.3 Probability distribution of departure time and access time of EV

图4 考虑随机特性与不考虑随机特性时的充电功率Fig.4 Charging power with and without stochastic characteristic

3.3 V2G对电网调度的影响

为了研究V2G对电网调度的影响，对以下3种调度模式进行对比分析。

模式1：对电动汽车进行无序充电方式，即电动汽车接入后立即进行充电直至满足充电需求，不考虑电动汽车的反向放电。

模式2：对电动汽车进行协调充电方式，即控制电动汽车的充电时间，优化系统负荷的同时满足充电需求，不考虑电动汽车的反向放电。

模式3：电动汽车采取V2G技术进行优化调度，即电动汽车接入电网后根据电网需求进行充电和放电的优化调度。

图5给出3种模式下各时段的系统负荷值以及无电动汽车时系统原负荷，表2—4给出了3种模式下机组的启停情况。由于I1、I2机组出力比较大，占全部机组的50%左右，所有时段都处于开机状态，因状态，对应24个时段，后同。

图5 3种模式下的系统负荷对比Fig.5 System load comparison among three modes

机组编号机组启停情况I30 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0I40 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0I50 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1I60 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0I70 0 0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 0 1 1 1 0 0 0I81 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 1 0 0 0 0I90 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 1 0 0 0 0I100 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0

注：表中“1”表示机组处于开机状态，“0”表示机组处于停机

表3 模式2机组启停情况Table 3 Unit start/stop situation under Mode 2

表4 模式3机组启停情况Table 4 Unit start/stop situation under Mode 3

此在表中不作说明。I8—I10小机组开机时间较少，在负荷较小阶段不用开机，为降低成本，只在负荷高峰期用以调峰作用。

从表2— 4可看出，模式1下的I8、I10机组开机时段要比模式2、模式3多；模式2下的I9机组比模式3的I9机组多出2个开机时段。对比模式1的无序充电，模式2实行协调充电后合理安排了电动汽车的充电时间，避免了电动汽车在负荷高峰期充电，在负荷低谷进行充电起到一定的填谷作用。模式3在实行V2G技术后，比模式2协调充电方案的负荷曲线更加平缓，电动汽车不仅能在负荷低谷时进行充电，而且在系统负荷高峰期进行放电，减少系统的负荷压力，调整各时段机组的出力，减少昂贵机组的开机时间，能有效减少机组成本，同时也具有环保效益。最终，模式1下的系统总成本为591 905.71，模式2下的系统总成本为571 467.38，模式3下的系统总成本为564 841.682。由此可见，采用V2G能够有效地降低成本。

3.4 电动汽车分类的研究

为了验证对电动汽车分类能使调度决策更加合理，采用以下5种方案进行分析对比。

方案1：所有车型的行驶特性均考虑为私家车。

方案2：所有车型的行驶特性均考虑为公交车。

方案3：所有车型的行驶特性均考虑为公务车。

方案4：所有车型的行驶特性均考虑为出租车。

方案5：考虑多类型电动汽车的行驶特性，即本文采用的模型。

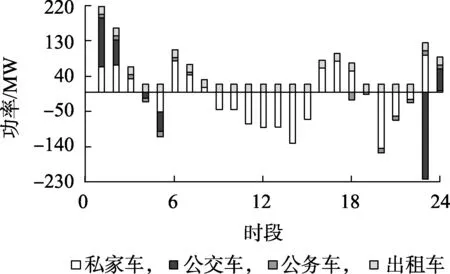
图6 各类型电动汽车充放电功率分布Fig.6 Charging and discharging power distribution of various types of EV

图7 5种方案下电动汽车的充放电功率对比Fig.7 Charging and discharging power comparison of EV under five cases

4 结论

本文分析了各类型电动汽车的随机特性，建立了考虑各类型电动汽车随机特性的机组组合模型，该模型以火电机组总成本最低为目标函数，电动汽车的随机特性通过模拟大量场景生成，并代入电动汽车相关约束中，在10机组系统仿真下得到优化结果，并得出如下结论：

a. 在对电动汽车进行合理调度时，需要考虑电动汽车的随机特性，调度人员应该在满足电动汽车随机出行规律情况下进行合理的充放电安排；

b. 运用V2G技术，能够起到削峰填谷的作用，使得机组的出力调整更加灵活，从而实现系统总成本最优；

c. 不同类型的电动汽车具有不同的出行特性，进行机组组合优化时需要考虑车辆的类型以及各类型车辆的出行特性。

附录见本刊网络版(http:∥www.epae.cn)。