波形钢腹板-钢管混凝土翼缘组合梁桥疲劳性能的 多尺度有限元分析

王志宇，张 涛，姜瑞娟，董桔灿，李晓磊，盖卫明

(1. 四川大学建筑与环境学院，四川成都 610065； 2. 大连理工大学海岸和近海工程国家重点实验室， 辽宁大连 116024； 3. 深圳市市政设计研究院有限公司，广东深圳 518029)

0 引 言

波形钢腹板具有较好的抗剪强度和稳定性、低压缩刚度等特点，可实现减轻自重和提高预应力效率[1]。中国自2005年引入这种结构以来，在波形钢腹板桥梁建设中得到了广泛应用[2]，桥梁跨径逐渐增加，其中最大跨径超过100 m的工程案例也越来越多涌现。在工程实践中，传统波形钢腹板组合箱梁的混凝土翼缘板在正弯矩作用下容易过早开裂[3-4]，从而降低了结构承载力、刚度及整体性，影响结构耐久性，也限制了波形钢腹板的优点进一步发挥。钢管混凝土充分发挥了钢与混凝土的力学性能优点，作为梁翼缘可在负弯矩区受力时避免侧扭失稳，亦可在正弯矩区受力时提高弯曲刚度，与波形钢腹板结合可更有效提高稳定性，避免混凝土翼缘板开裂，这种结构形式已应用于法国Maupre桥。

随着波形钢腹板-钢管混凝土翼缘组合梁桥跨度提高，交通量日渐增大，疲劳设计和疲劳寿命预测也成为了组合结构在桥梁设计和安全评估中的关键技术之一[1]。调查表明结构局部细节部位的细观缺陷、损伤演化和积累是桥梁疲劳失效的主要原因。结构疲劳分析主要可通过有限元数值模拟和模型试验实现。有限元方法以线性疲劳累积损伤理论和线弹性断裂力学理论为基础，通常采用三维实体单元能较好预测结构的疲劳寿命和裂纹扩展，但较大结构模型分析往往存在计算量大、耗时长的问题。为更好优化分析，早期国内外学者主要对子模型法进行研究，探讨了边界条件及其精确度的实现[5-8]，随后多尺度有限元模型在桥梁损伤力学分析中被较多关注。这种方法将精细化尺度模型嵌入到大尺度模型中去，可在同一模型中实现整体结构分析和局部构件分析同步开展，一次计算获得多种分析结果，提高了计算效率，达到计算精度，已成为目前研究热点问题。李兆霞等[9]以香港青马大桥和江苏润扬长江大桥为依托，进行了结构健康监测和状态评估，实现了从局部损伤劣化、结构多尺度和时空多尺度方面的分析。还有相关研究将这种方法与损伤评价相结合以评定模拟大型结构健康监测和损伤[10]；采用Arlequin方法模拟桥钢桁加劲梁、节点板等局部与整体耦合区域，提高模拟效率等[11-12]。

本文采用有限元软件对波形钢腹板-钢管混凝土翼缘组合梁进行多尺度建模，利用参照点来约束耦合面上的耦合以实现不同尺度模型之间的变形协调，并进而实现多尺度应力场分析，实现局部精细模型和整体结构模型相结合。通过对局部模型试验结果验证，对局部模型进行了修正。分析结果表明，采用多尺度有限元分析可较好地应用于这种结构的疲劳分析中，能提高计算效率和模拟精度。该方法有效地模拟局部精细单元的应力集中，并进而进行基于断裂力学的寿命分析，为波形钢腹板-钢管混凝土翼缘组合梁的抗疲劳设计提供依据。

1 工程背景

深圳马峦山公园1号桥(图1)地处深圳市大山陂-矿山水库南侧水源保护区内，为设计车速80 km·h-1、车辆荷载城-A级、设计基准期100年、安全等级一级的城市快速路配套工程。为了避免现浇混凝土施工期间对场地环境的不利影响，采用波形钢腹板-钢管组合梁新型结构，波形钢腹板-钢管组合梁新型结构由混凝土顶板、下弦钢管和波形钢腹板连接组成。该桥由深圳市市政设计研究院有限公司独立设计，分为左、右两幅，左幅为45 m简支梁，右幅为3×45 m连续梁。每幅箱梁均为双箱单室断面，单幅桥面宽度20 m=2 m(检修道及栏杆)+16 m(行车道)+2 m(检修道及栏杆)，跨中处梁高2.8 m，横梁处梁高3 m；底缘采用720×20 mm钢管混凝土；腹板采用1600型波形钢腹板，钢材为Q345qC；支点处设置混凝土横梁，梁宽1.2 m。深圳马峦山公园1号桥均采用波形钢腹板，钢材采用Q345qC，板厚为12～24 mm。

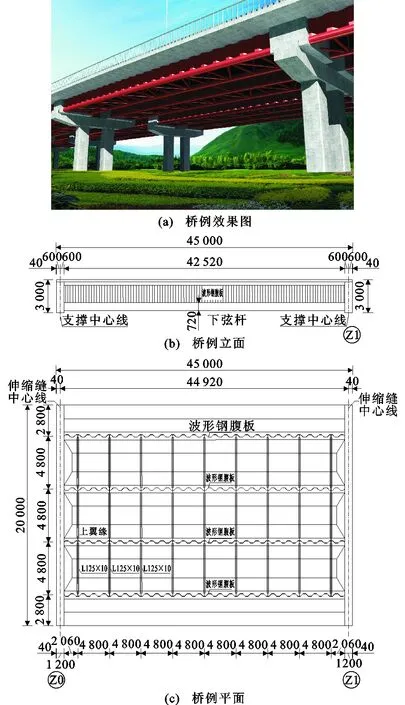
2 结构多尺度模型构建

2.1 计算方法

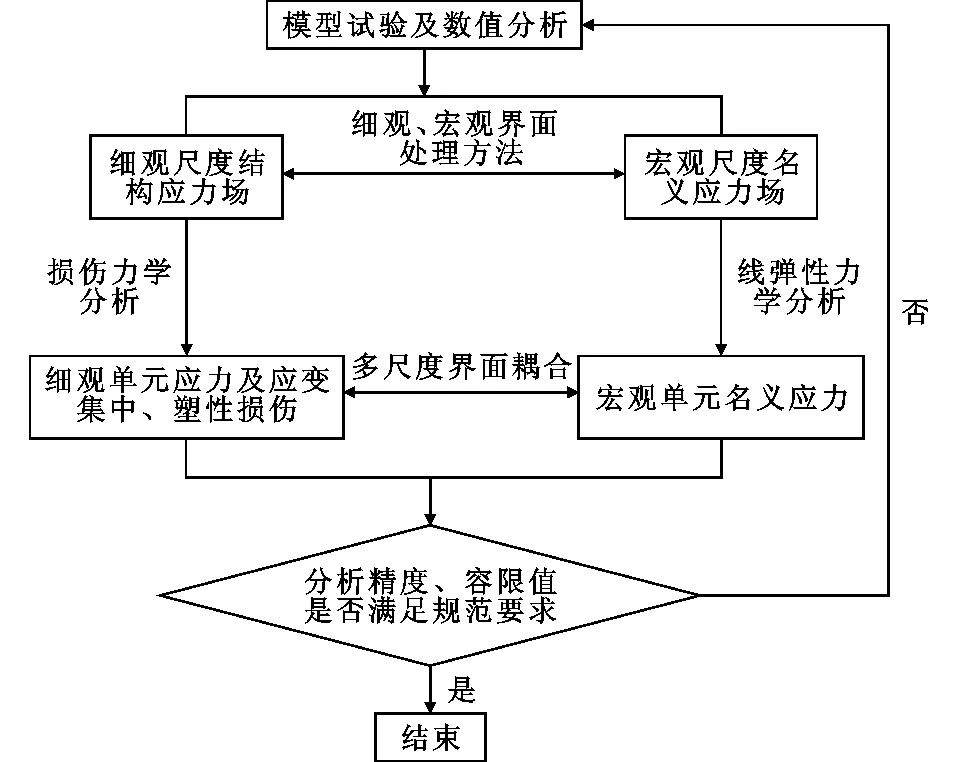
结构多尺度分析计算的主要思路是合理选取一定代表性单元，通过不同尺度的界面连接，实现对实桥整体和局部结构同步分析。将该计算方法应用于依托工程的分析流程如图2所示。在计算分析时，根据对工程桥梁缩比试验和数值分析，按宏观尺度建立模型进行全桥线弹性分析，获取整体结构的基本受力行为，以及波形钢腹板、钢管混凝土翼缘及其连接部位的应力分布规律，提取对疲劳受力较为不利的组件及连接部位。针对这些可能存在塑性发展和损伤的部位进行细部分析，通过小尺度单元构建结构组件及细部有限元模型以反映疲劳裂纹和损伤的可能扩展路径、应力分布方式等。通过损伤力学分析，获得相关应力集中模式、塑性及损伤发展规律等。为实现不同尺度单元联系，建立协调条件或平衡方程，使不同自由度的单元之间能有跨尺度边界条件相连，包含一套细观、宏观界面处理方法，以及多尺度截面耦合方法，从而使有限元分析时既能获得整体模型在名义应力下的基本受力特征，还可以对易损部位进行精细化分析，考虑损伤演化对整体结构的影响，能对相关影响几何和构造参数进行充分考虑。

2.2 界面连接

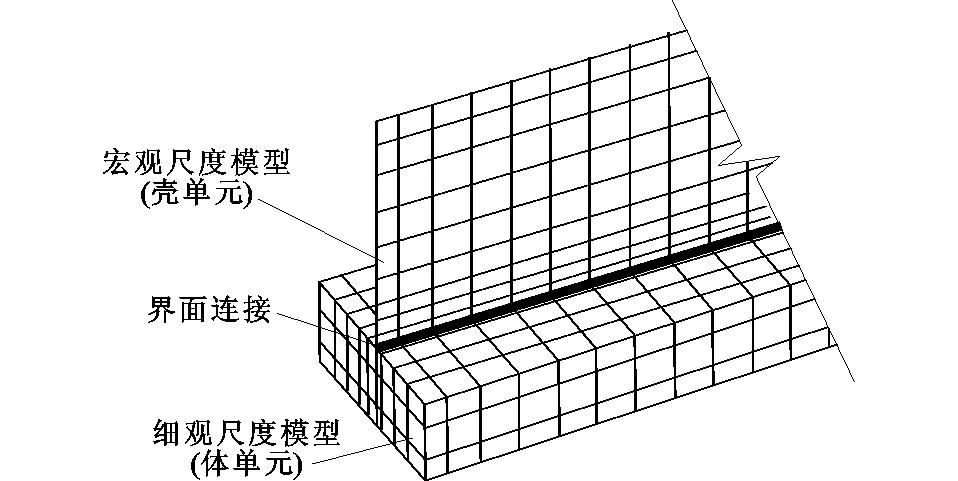
多尺度模型构建中不同单元之间界面连接是分析的关键。要点在于宏观与细观界面处不同单元节点自由度能保持变形协调。本文分析中采用细观尺度模型离散为体单元，宏观尺度模型离散为壳单元，这2种约束之间采用多点约束，如图3所示。这种约束是一种节点自由度的耦合关系，即以一个节点的某几个自由度为标准值，然后令其他指定节点的某几个自由度与这个标准值建立某种关系。多点约束用于表征刚性连接，也可用于不相容单元间的荷载传递，是一项重要的有限元建模技术。

壳体与实体单元连接通过多点约束时，必须激活剩余约束，并假设界面连接处壳体节点位移等于实体厚度上所对应节点位移，壳体节点转动与实体沿厚度方向所对应的节点转动相协调。对于壳体节点位移约束，可表示为壳体节点位移δs等于实体内节点位移δc加权值，即

(1)

式中：wi为与多点约束类型相关的权重值。

如今，老胡凭藉厚实之馆藏及数次举办相关展览而整理、觅宝获得的照片，倾几年之精力，以更全面、扎实的作业呈现其成果，辑为《中国抗战话剧图史（1931-1945）》。众所周知，我国抗战期间话剧或戏剧论著甚多，然录之以图像者则鲜有见者。传敏先生等所编之书，补白价值显然。图史以上海、武汉、重庆、桂林和延安为中心，以话剧为视角，以数百幅老照片为载体，典型、专业而又形象地展示了中国共产党领导下“文化抗战”的真实景象。既光大抗战精神，又拓展资料学术含量，无论于戏剧界或文献界均贡献良多，功莫大焉。

对于壳体节点的转动约束，可假设实体相交部位的节点在同一直线上，N，n与a关系可表示为

eǎN=n

(2)

式中：ǎ为转动向量a的反对称矩阵；N为线上节点不变形面的法向量；n为变形面的法向量。

若以上约束方程还不能完全定义壳体节点转动，还可再增加一个沿实体边线的转动量，线性转动约束形式可表示为

ndθ=dn

(3)

式中：dθ为线性转动量。

若将与n垂直方向定义为纵向、横向分别为s和t的局部坐标系，则将式(3)投影到该局部坐标系上可表示为

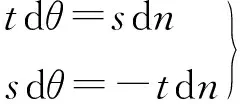
(4)

可得到法向方向上最大位移δn和最小位移δ1差值满足

(5)

将式(5)代入式(4)可得

(6)

将局部三维向量dθ表达式进行转换，可得出针对总体向量dθ的约束方程为

(7)

式中：下标i,j,k分别为线性转动量对应于局部坐标系x,y,z的3个分量。

若以dθk为变量求解方程式(7)，可得

(8)

通过以上方程式(8)可描述壳体与实体单元之间的变形协调，便于在几何线性分析中对线性方程进行定义。

3 有限元模拟

3.1 模型信息介绍

波形钢腹板及其连接焊缝在波形的平直段与倾斜段过渡段部位的应力集中往往成为波形钢腹板梁受弯下疲劳失效的主要因素，王志宇等[13]提出以波形钢板焊接连接件拉伸疲劳试验的方法为评价波形钢腹板梁的疲劳寿命提供了关键参考。试验应力数据可分解为多个与波形特征相关的应力集中系数，建立几何效应与应力特征关系，通过断裂力学方法对结果进行处理，便可得到波形钢腹板梁的疲劳寿命及其影响参数。由此本文有限元模型研究主要针对波形的平直段与倾斜段过渡段部位建立宏观模型、精细化模型、多尺度模型。

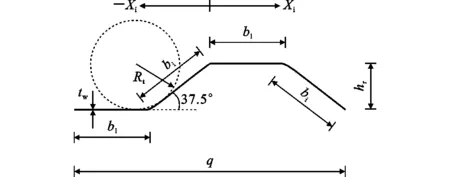
采用本模型分析时按以下假设[14]：波形钢腹板的抗弯能力可忽略；钢管与混凝土不存在相对滑移，可被视为共同工作。参考相关波形钢腹板设计规范[15]和钢结构设计规范[16]，对依托工程主梁的中跨段进行缩比，纵向跨度取为3.058 m，钢管截面尺寸为150 mm×100 mm×5 mm，上、下翼缘均由波形钢腹板与钢管混凝土焊接而成。所选混凝土等级为C50，从受力情况推估正弯矩下钢管内混凝土受拉对梁弯曲承载力贡献较小，但对翼缘刚度提高较为有利。波形钢腹板高度hw取值为400 mm。作为基准参数，波形角θc=37.5°，波形平直段长度bl与倾斜段长度bi均为140 mm，可换算波形高度hr=104 mm，腹板厚tw=3 mm，波形钢板高厚比hw/tw取值为133.33，单位波长波形水平投影长为q，如图4所示。波形转角曲率半径Rt取值为0.25hr=26.08 mm，0.75hr=78.26 mm。试件钢材为Q345，弹性模量取为2.06×105MPa，泊松比为0.3。

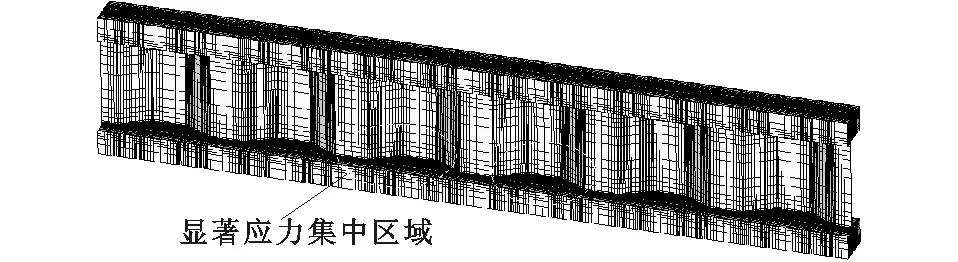
采用有限元程序ANSYS建立波形钢腹板-钢管组合梁的三维计算模型，如图5所示。针对宏观模型和精细化模型，钢管翼缘、波形钢板及连接角焊缝分别采用Shell63壳体单元和Solid95实体单元模拟，填充混凝土采用Solid65实体单元模拟，在正弯矩最大区域的应力集中显著区域采用较细密度的网格，而较远区域采用相对较粗的网格密度以减小有限元运算量。

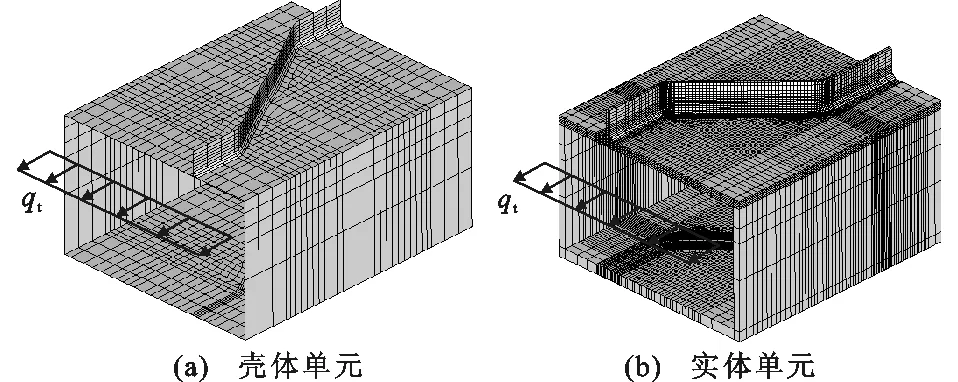
对于波形钢腹板-钢管翼缘焊接连接细节模型，分别采用壳体和实体单元对1/2单位波长的波形钢板焊接连接件进行有限元建模及网格划分[14]，如图6所示。在模型分析中，考虑正弯矩作用在钢管翼缘上产生等效拉应力qt，而不考虑混凝土抗拉贡献。

对于组合梁的多尺度建模，首先通过宏观模型分析对应力集中显著区域进行识别，然后对该区域建立精细化波形钢腹板-钢管翼缘焊接连接细节模型。为实现精细化模型与宏观模型之间截面有效连接，保持两者在连接界面上具有相同运动协调性，采用多点约束实现壳体单元和实体单元界面可靠连接，如图7，8所示。实体单元边界上节点满足如下规律

[δxk，i，δyk，i，δzk，i]′=[δxt，i，δyt，i，δzt，i]′

i=1,2,…,n

(9)

[θxk，i，θyk，i，θzk，i]′=[θxt，i，θyt，i，θzt，i]′

i=1,2,…,n

(10)

式中：δxk,i，δyk,i，δzk,i分别为壳体在约束面上x，y，z方向的位移；θxk,i,θyk,i,θzk,i分别为壳体在约束面上x,y,z方向的转动量；δxt，i，δyt，i，δzt，i分别为体单元在约束面上x,y,z方向的位移；θxt，i，θyt，i，θzt，i分别为体单元在约束面上x,y,z方向的转动量。

3.2 疲劳寿命分析

局部应力达到破坏水平则认为结构出现了疲劳破坏，其寿命为循环周次为N0。疲劳寿命使用系数的定义为有限循环周次N与破坏周次的比值，即N/N0。有限元计算步骤如下：根据静力应力云图的分布得出结构应力集中部位的最大(最不利)应力，列出危险部位相邻区域20个相关对象节点号，并分别对其节点应力数据进行提取；设置事件重复次数并与疲劳寿命使用次数项对应，通过循环判断是否达到结构疲劳寿命；对照所定义的应力-循环周次(S-N)曲线获得所有对象节点的疲劳寿命，比较得出最不利疲劳寿命使用系数，并换算得出该部位疲劳寿命。应力幅ΔS为135 MPa和165 MPa时由壳体单元定义的宏观模型、由实体单元定义的细观模型和多尺度模型计算得出的疲劳寿命值见表1。由文献已有的疲劳寿命数据，可通过回归方法得到S-N关系式为：lg(N)=12.68-3lg(ΔS)[13]。按此经验公式换算得出应力幅为135 MPa和165 MPa所对应的寿命分别为1 945 354，106 548 7。对于腹板-翼缘连接细节建模，采用壳体单元模型、实体单元模型和多尺度模型的有限元预测寿命与经验公式预测寿命比值分别为1.23，0.94，0.96(ΔS=135 MPa)，以及1.23，0.94，0.96(ΔS=165 MPa)。对于梁结构建模，采用壳体单元模型、实体单元模型和多尺度模型的有限元预测寿命与经验公式预测寿命比值分别为1.32、1.03和1.08(ΔS=135 MPa)，以及1.35，1.1，1.12(ΔS=165 MPa)。由此可见，采用壳体单元模型的预测值与理论疲劳寿命预测值差别最大，而采用实体单元模型和多尺度模型的疲劳寿命预测值较为接近。

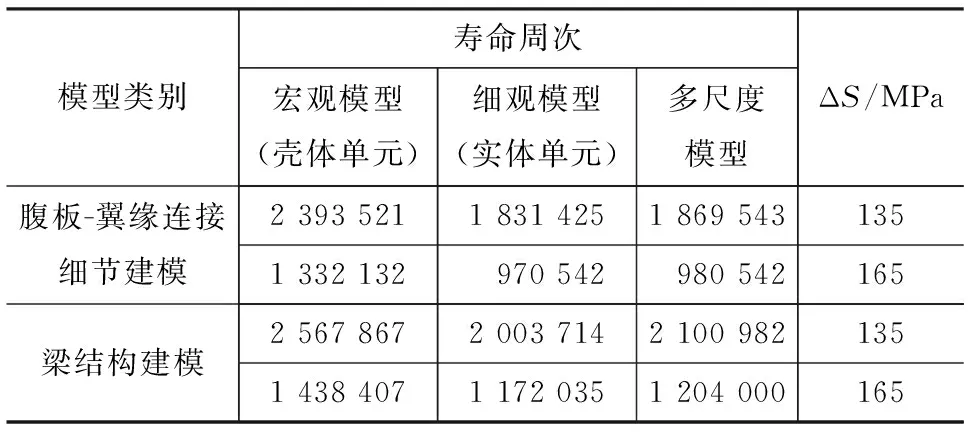
表1 不同模型计算寿命对比Tab.1 Computational Life-time of Different Models

表2为不同模型的计算分析时间对比，可见：对于波形钢腹板-翼缘连接细节建模，采用多尺度模型的平均计算分析时间比细观模型节约28.9%；对于梁结构建模，采用多尺度模型的平均计算分析时间比细观模型节约40.7%。因此，多尺度模型不仅能较准确对腹板-翼缘连接细节和梁结构疲劳寿命进行预测，还能兼顾计算分析的效率。

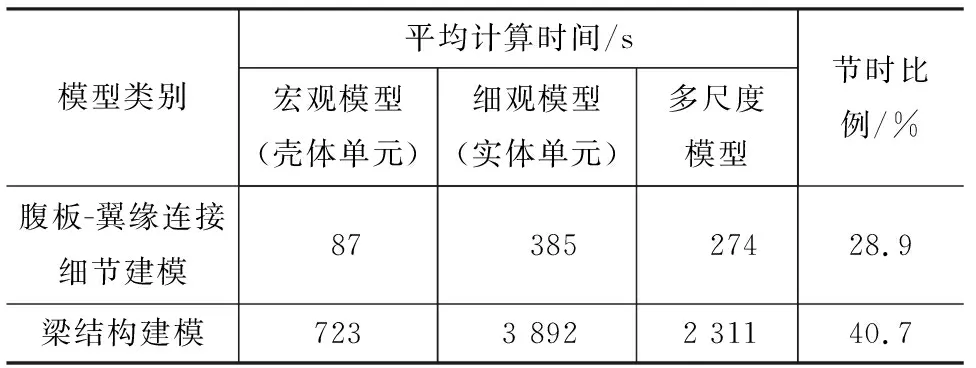
表2 不同模型计算分析时间对比Tab.2 Computational Time of Different Models

4 波形钢腹板-钢管翼缘连接部位应力场特性分析

本文所参考常见的疲劳破坏模式发生于波形钢腹板-钢管翼缘连接部位，裂纹萌生位于近波形钢腹板倾斜段终点部位的焊趾处，几乎与母材板面的拉应力方向垂直[13]，如图9所示。波形钢腹板梁在弯矩作用下钢管翼缘上疲劳裂纹垂直于等效受拉应力，经扩展、聚合、再扩展，逐渐由小裂纹发展为统一的断口。对单位波长波形范围内，沿波形板焊趾连接失效部位的主应力进行提取，对比分析波形角θc=30°，45°时局部应力集中特性，如图10，11所示。为方便对比，对连接部位处的钢管翼缘均施加100 MPa的名义应力，应力集中系数为路径分布最大应力值与名义应力100 MPa的比值。

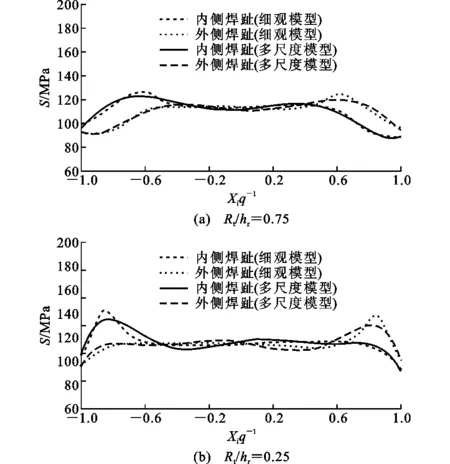
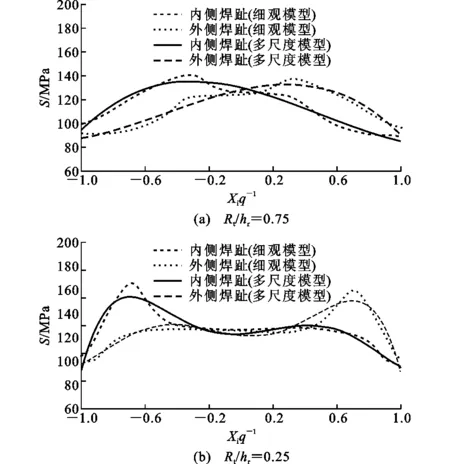
从总的趋势看，主应力沿内侧焊趾和外侧焊趾的应力分布情况呈对称分布，最大值均出现在波形钢板倾斜段终点处，介于平直段与倾斜段的过渡段部位，与试验中所观察的疲劳破坏部位一致。对比图10，11中细观模拟结果可知：随着波形转角曲率半径与波形高度比值Rt/hr由0.75降低至0.25，波形钢板焊接连接的应力集中系数提高到1.13倍左右，分别由1.27提高到1.44(θc=30°)和1.40提高到1.65(θc=45°)；随着θc由30°提高到45°，波形钢板焊接连接的应力集中系数增大幅度约为4%，分别由1.27提高到1.40(Rt/hr=0.75)和1.44提高到1.65(Rt/hr=0.25)。从最大应力分布看：多尺度模拟结果相比细观模拟结果稍微偏小，当θc=30°时，多尺度模拟应力结果低估约2%；当θc=45°时，多尺度模拟应力结果低估约5%。多尺度模拟主应力分布总趋势与细观模拟结果非常接近，可较为准确地模拟最大(最不利)应力情况，由此可为直观有效把握局部疲劳损伤演变和裂纹开展过程等提供有效参考。

5 结 语

(1)通过对深圳马峦山公园1号桥波形钢腹板-钢管混凝土翼缘组合梁的疲劳性能分析，分别针对波形钢腹板-翼缘连接细节和梁结构建立了细观和宏观分析模型，对多点约束界面连接及多尺度模型构建过程进行了分析和探讨，结合有限元分析对其疲劳寿命预测精度和计算分析效率进行了对比。结果表明：对于波形钢腹板-翼缘连接细节建模，采用多尺度模型计算分析时间比精细化模型可节约28.9%，而寿命预测相对误差可控制在2%以内；对于梁结构建模，采用多尺度模型计算分析时间比精细化模型可节约40.7%，而寿命预测相对误差可控制在5%以内。在不影响疲劳寿命预测精度的前提下，采用多尺度有限元模型可较为有效地提高计算分析效率。

(2)结合多尺度模型对波形钢腹板-钢管翼缘连接部位应力特性进行了研究，对比了波形角以及波形转角曲率半径与波形高度比值对模拟结果的影响。结果表明，随着波形转角曲率半径与波形高度比值由0.75降低至0.25，波形钢板焊接连接的应力集中系数提高到1.13倍左右；随着波形角由30°提高到45°，波形钢板焊接连接的应力集中系数增大幅度约为4%；多尺度模型模拟连接部位主应力分布规律与精细化模型一致，最大主应力值相对误差在5%以内，因此多尺度模型可较有效地为波形钢腹板-钢管混凝土翼缘组合梁的疲劳损伤分析提供参考。