基于MCFT的高强轻骨料混凝土框架中节点 受剪承载力计算方法

吴 涛，王立勋，刘 喜

(长安大学建筑工程学院，陕西西安 710061)

0 引 言

高强轻骨料混凝土拥有密度低、强度高、保温效果显著、抗裂效果明显等优点，具有良好的应用前景，已广泛应用于高层建筑、桥梁工程等[1-4]，但其弹性模量低，脆性大，易发生剪切破坏，尤其是在往复荷载作用下抗剪强度明显降低。对比中国《轻骨料混凝土结构技术规程》(JGJ 12—2006)[5]和《混凝土结构设计规范》(GB 50010—2010)[6]可以发现，轻骨料混凝土节点核心区的受剪承载力计算公式由普通混凝土公式中混凝土项和轴力项进行75%的折减得到，缺乏合理的理论支撑。

高强轻骨料混凝土框架中节点受力机理相对复杂，抗剪强度受多种条件影响，包括混凝土等级、轴压比、核心区配箍率等[7-10]，目前中国设计规范实际采用的承载力计算公式是基于经验和理论回归基础上提出的[6,11]，缺乏合理的理论支持。然而加拿大学者Vecchio等[12-15]在压力场理论(CFT)基础上，依据应力平衡方程、应变协调方程及材料本构关系，进一步考虑混凝土裂缝之间残余拉应力，推导出了修正压力场理论(MCFT)，且已证明其在混凝土构件受剪性能分析中效果显著，其核心思想已被海外多部规范采纳，包括美国标准AASHTO、加拿大CSA A23.3-04规范等[16-17]。

基于此，本文进行了4个高强轻骨料混凝土框架中节点试验研究，对该类构件的破坏模式和破坏过程进行了理论分析，同时在修正压力场理论(MCFT)基础上，推导出高强轻骨料框架中节点受剪计算模型，完成包含本文构件在内的17组高强轻骨料混凝土框架中节点的受剪承载力计算，以及试验结果与计算结果的对比分析。

1 试验概况

1.1 试件设计

试验设计了4个高强轻骨料混凝土框架中节点试件，试件上柱和下柱高度均为1 050 mm，左右两侧横梁长度均为1 200 mm。试件采用了不同的节点核心区配箍率。试件配筋情况如图1所示，试件详细设计参数见表1。

试件由强度等级为LC40的高强轻骨料混凝土浇筑，其水泥采用P.O42.5普通硅酸盐水泥，轻骨料使用强度800级页岩陶粒，陶粒粒径分布在5～16 mm之间， 陶粒筒压强度为6.2 MPa，细骨料由

表1 试件参数Tab.1 Parameters of Specimens

注：bc,hc分别为框架柱的截面宽度和高度；bb,hb分别为框架梁的截面宽度和高度；ρct,ρcl分别为节点核心区的水平和竖向配筋率；ρbt,ρbl

分别为节点水平和竖向配筋率；ρj为体积配箍率。

普通砂和陶砂按3∶1比例混合配置。试件箍筋为HPB300级钢筋，纵筋为HRB400级钢筋。试件的混凝土配合比见表2，试件高强轻骨料混凝土参数见表3。

表2 高强轻骨料混凝土配合比Tab.2 Mix Proportion for High-strength Lightweight Concrete

表3 高强轻骨料混凝土参数Tab.3 Parameters for High-strength Lightweight Concrete

注：fcu为混凝土立方体抗压强度；fck为混凝土轴心抗压强度标

准值；ftk为混凝土轴心抗拉强度；Ec为混凝土弹性模量。

1.2 试验结果

各试件在水平低周往复荷载作用下均在节点核心区发生了剪切破坏。虽然各试件的核心区配箍率和轴压比不尽相同，但在低周往复荷载作用下，破坏过程都与普通混凝土相似，均依次产生了初裂、通裂、极限和破坏4个典型阶段。试件典型阶段特征荷载及剪切变形见表4。

1.3 破坏形态

以试件HSLCJ-1的试验现象为例，阐述该类试件的剪切破坏形态。加载初期，试件处于弹性受力阶段，首先产生垂直于梁跨度方向的弯曲裂纹。随荷载增加，节点核心区逐渐开裂，并不断发育形成第1条斜裂缝，此刻进入初裂阶段。持续加载，节点核心区在对角线方向出现交叉裂缝，并且稳定发展，形成0.14 mm宽的主斜裂缝，持续发展至0.5 mm，节点进入通裂阶段。此后节点核心区裂缝持续增多，且开始逐渐向柱方向延伸，剪切变形显著变大，核心区开始出现起皮、脱落现象，试件迅速进入极限状态，承载能力达到最大值。荷载继续施加，核心区混凝土出现大块脱落、箍筋外露现象，最后试件核心区形成X形主斜裂缝。正向主斜裂缝增至1.6 mm宽，反向主斜裂缝增至1.2 mm宽。随着交替变形的缓慢增大，荷载也缓慢下降，混凝土大量脱落，变形急剧变大。当柱端荷载减小至其极限荷载的85%时结束加载。最终，左右梁破坏形态呈对称分布，核心区损伤严重，混凝土被压碎，是典型的核心区剪切破坏。试件的破坏形态如图2所示。

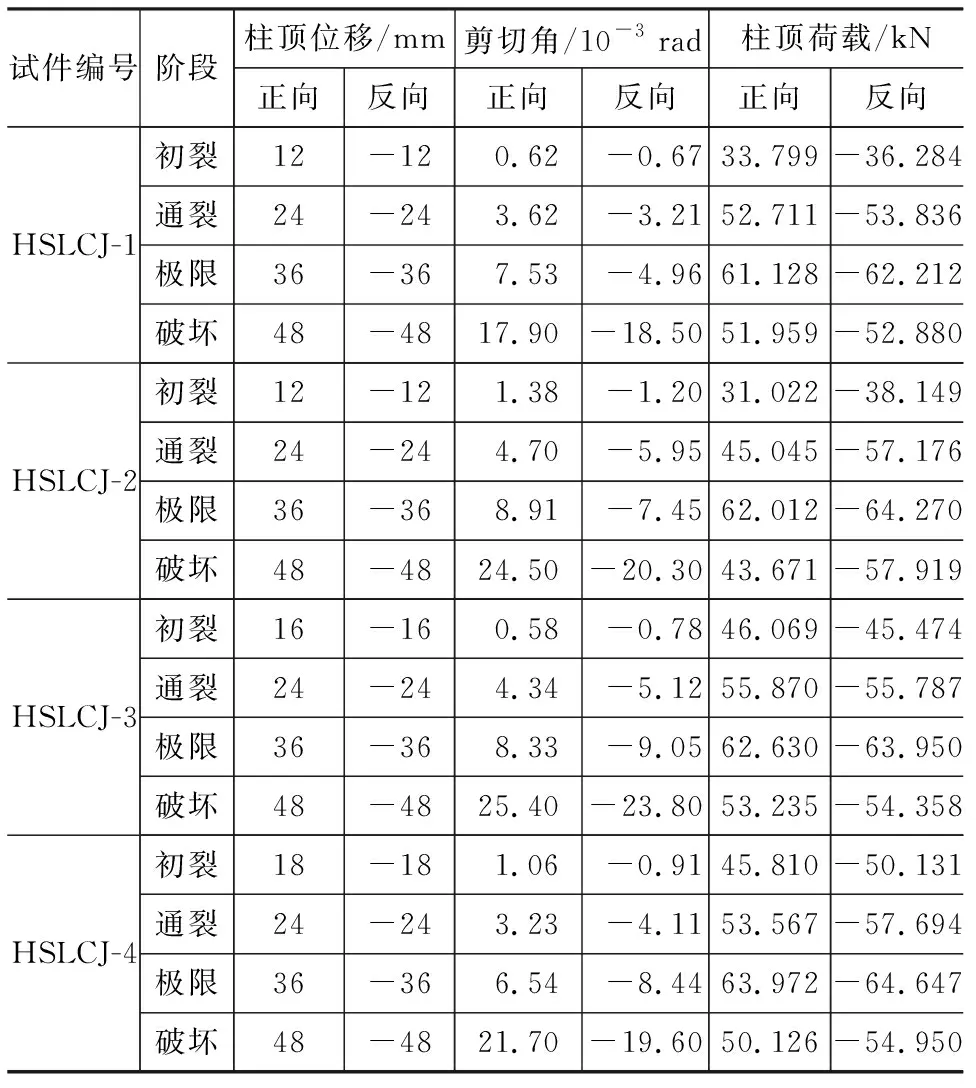
表4 试件典型阶段特征荷载Tab.4 Eigenvalues Loads of Specimens in Typical Stages

2 MCFT模型建立

2.1 平衡条件

由钢筋和混凝土共同承担作用于钢筋混凝土薄膜单元的外力，且忽略因为钢筋存在而引起的混凝土截面面积的微小变化，由图3可得2个方向的平衡方程为

fx=fcx+ρsxfsx

(1)

fy=fcy+ρsyfsy

(2)

vxy=vcx+ρsxvsx

(3)

vxy=fcy+ρsyvsy

(4)

式中：fx,fy,vxy分别为x向、y向、合力方向的外力；fcx，fcy分别为x向、y向的平均应力；ρsx，fsx分别为x向钢筋的配筋率和应力；ρsy，fsy分别为y向钢筋的配筋率和应力；vsx，vsy分别为x向、y向的剪应力。

假定节点核心区钢筋只承受拉应力和压应力，不承担任何方向上的剪应力，即vsx=vsy=0，据此可以得到如下方程

vcx=vcy=vcxy

(5)

图4为开裂后混凝土薄膜单元平均应力莫尔圆，其中v为剪应力，f为剪应变，θc为主压应力倾角。利用平均应力莫尔圆中的几何关系以及图4可以得到

fcx=fc1-vcxy/tan(θc)

(6)

fcy=fc1-vcxytan(θc)

(7)

fc2=fc1-vcxy[tan(θc)+1/tan(θc)]

(8)

式中：fc1，fc2分别为混凝土主拉应力和主压应力。

2.2 相容条件

假设节点核心区钢筋完全锚固于混凝土中，两者不发生黏结滑移，即钢筋与混凝土具有完全相同的变形量，因此有

εsx=εcx=εx

(9)

εsy=εcy=εy

(10)

由图5所示的几何关系可以得到

(11)

ε1+ε2=εx+εy

(12)

(13)

式中：εx，εy分别为x向和y向应变；εsx为箍筋应变；ε1，ε2分别为主拉应变和主压应变；θ为主压应变方向角；γxy为剪应变。

2.3 本构关系

钢筋本构关系可表示为

fsx=Esεx≤fyx

(14)

fsy=Esεy≤fyy

(15)

式中：Es为钢筋弹性模量；fyx,fyy分别为x向和y向的屈服强度。

高强轻骨料混凝土受压时选用Vecchio建议的裂缝间平均应力-应变关系模型，即

(16)

开裂混凝土平均主拉应力fc1为

(17)

2.4 裂缝间力的平衡

假设节点核心区斜裂缝相互平行，均与纵向钢筋呈θ角度。混凝土裂缝处局部应力和混凝土计算平均应力如图6所示。当施加外力fx，fy和vxy后，由x向和y向力平衡得

ρsx(fsxcr-fsx)=fc1+fci+vci/tan(θ)

(18)

ρsy(fsycr-fsy)=fc1+fci-vcitan(θ)

(19)

式中：vci为开裂混凝土的局部应力；fsxcr,fsycr分别为裂缝x向和y向的钢筋应力；fci为混凝土裂缝处的压应力。

当裂缝截面处既无剪应力又无压应力作用时，式(18)，(19)应满足

ρsy(fsycr-fsy)=ρsx(fsxcr-fsx)=fc1

(20)

裂缝间钢筋应力应当小于屈服强度，即fsxcr≤fyx，fsycr≤fyy,由此证明裂缝间存在剪力，可得主拉应力fc1应满足以下控制条件

fc1≤vci,max(0.18+0.3k2)tan(θ)+ρsy(fyy-fsy)

(21)

式中：k=1.64-1/tan(θ)，且k>0。

开裂混凝土的局部剪应力vci可通过下式计算

(22)

(23)

式中：a为骨料的最大粒径；混凝土裂缝处压应力fci的计算方法参考文献[13]；w为裂缝宽度。

本文计算模型对公式(23)中骨料粒径参数a进行了修正，由于轻骨料混凝土中的骨料会破碎，裂缝由骨料内部经过，故此时取a=0进行计算[18]。

公式(23)中裂缝宽度w可由下式求得

w=ε1sθ

(24)

(25)

(26)

式中：sθ为混凝土薄膜单元裂缝的平均间距；smx，smy分别为垂直于x向和y向的裂缝间距；dx，dy分别为x向和y向的钢筋最大间距。

2.5 计算过程

将上述方程联立求解，即可得计算结果，MCFT计算流程如图7所示。

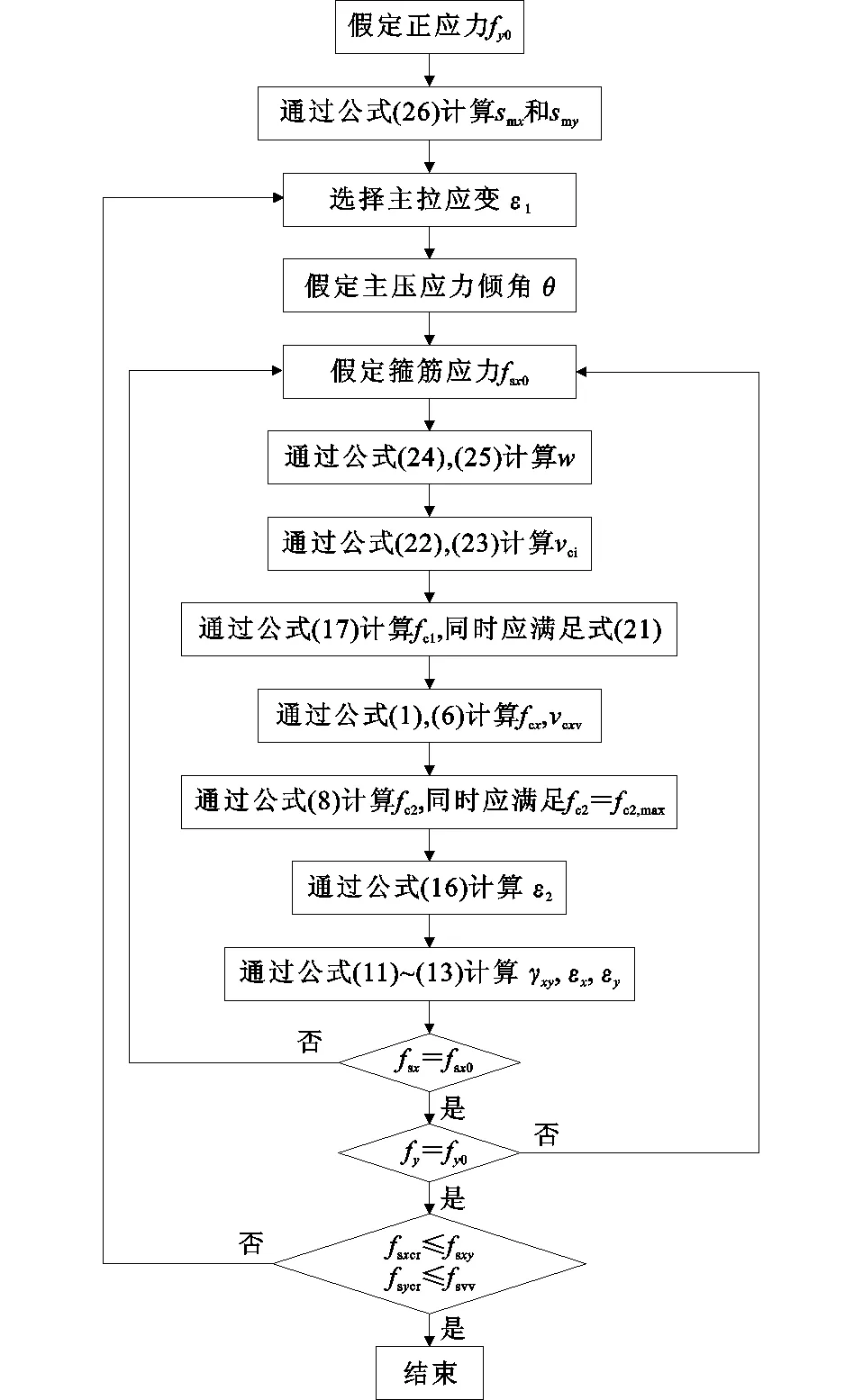
计算步骤包括：

(1)假定节点核心区y向正应力fy0。

(2)通过公式(26)计算核心区的裂缝间距smx和smy。

(3)选择合适的混凝土主拉应变ε1。

(4)假定主压应力倾角θ。

(5)假定箍筋应力fsx0。

(6)通过公式(24)，(25)计算平均裂缝宽度w。

(7)通过公式(22)，(23)计算裂缝间剪应力vci。

(8)通过公式(17)计算混凝土主拉应力fc1，同时应满足公式(21)控制条件。

(9)通过公式(1)，(6)计算fcx，vcxy。

(10)通过公式(8)计算fc2，同时应满足fc2≤fc2,max。

(11)通过公式(16)计算混凝土主压应变ε2。

(12)通过公式(11)～(13)计算εx，εy和γxy。

(13)通过公式(14)计算fsx，将fsx与步骤(5)假定的fsx0相比较，若fsx=fsx0，则继续计算，否则返回步骤(5)调整fsx0，直至fsx=fsx0。

(14)通过公式(15)，(2)计算fsy，fy，将fy与步骤(2)假定的fy0相比较，若fy=fy0，则继续计算，否则返回步骤(4)调整θ，直至fy=fy0。

(15)通过公式(18)，(19)计算裂缝面处钢筋应力fsxcr，fsycr，若其值小于钢筋屈服强度，则终止计算，否则返回步骤(3)，减小ε1后重新计算。

完成以上步骤，即可得一组节点核心区剪应力vcxy和剪切变形γxy，逐渐增大设定的节点核心区y向正应力fy0，即可得到节点核心区的剪应力-剪应变关系曲线。

3 试验验证

将上述计算过程编制MATLAB程序，对本文4个中节点进行受剪分析，由此得到试件节点核心区剪应力-剪应变曲线，模型获得的曲线与试验测得的曲线比较情况如图8所示。同时对本文和文献[19]～[21]共17组轻骨料混凝土框架中节点峰值剪应力进行计算，结果见表5。

由表5和图8可以看出，试件测试结果与MCFT计算模型模拟结果比值的均值和方差分别为0.907和0.008，MCFT计算模型计算获得的剪应力-剪应变关系曲线与试验得到的曲线在上升段吻合良好。需要注意的是，该模型计算结果偏高于试验结果，这主要是因为该模型将节点核心区按照相同的配筋方式等效为平面板单元进行计算，边界条件的变化致使模拟结果比实际稍高一点。另外发现模型计算曲线下降快于试验曲线，这是因为破坏阶段试验节点梁筋出现滑移，导致刚度和强度退化较慢，而本文MCFT计算模型中假设节点核心区钢筋完全锚固于混凝土中，两者不发生黏结滑移。

表5 高强轻骨料混凝土试件计算结果与试验结果对比Tab.5 Comparison of Peak Shear Stress Between Calculation Results and Test Results for High-strength Lightweight Aggregate Concrete Specimens

注：τtest为试验的剪应力；τMCFT为模型的剪应力。

4 结 语

(1)试验结果表明，该类高强轻骨料混凝土框架中节点破坏过程与普通混凝土相似，都经历了初裂、通裂、极限和破坏4个典型过程。

(2)应用修正压力场理论(MCFT)计算了17组高强轻骨料混凝土框架中节点峰值剪应力，结果表明计算值与试验值接近，可以应用于该类构件的极限受剪承载力预测。

(3)修正压力场理论模拟得到的剪应力-剪应变关系曲线与试验曲线在上升段吻合较好，且该理论有明确的力学理论和计算过程，可以较为清楚地反映构件初裂、通裂、极限阶段的受力过程。