基于马尔科夫链和列联表法的马尾松毛虫发生面积预测模型研究
高薇,余燕,毕守东,张国庆,邹运鼎
(1.国家林业局森林病虫害防治总站,林业有害生物监测预警国家林业局重点实验室,辽宁 沈阳 110034; 2.安徽农业大学理学院,安徽 合肥 230036; 3.安徽省潜山县林业局,安徽 潜山 246300; 4.安徽农业大学林学与园林学院,安徽 合肥 230036)
马尾松毛虫DendrolimuspunctatusWalker,分布于我国南方16个省区,主要危害马尾松Pinusmassoniana,还危害黑松Pinusthunbergii、火炬松Pinustaeda、湿地松pinuselliottii、晚松Pinusrigidavar.serotina、海南松Pinusfenzeliana等松属植物[1-4]。马尾松毛虫发生的预测预报是对其进行综合防治的基础工作。科技工作者[5-11]采用不同预测方法预测马尾松毛虫的发生量、虫害等级、发生类别、发生空间格局,为马尾松毛虫综合防治工作提供了有力支持。由于各地气象条件、植被条件和地形地貌等不同,马尾松毛虫的发生特点也不完全相同。发生面积是马尾松毛虫危害严重程度的一个重要标志,为了有效地防治马尾松毛虫,本文作者采用马尔科夫链法和列联表多因子多级分析法研究马尾松毛虫的越冬代、一代和二代发生面积,并对两种方法预测结果的优缺点进行比较,以期为马尾松毛虫综合治理提供科学依据。
1 材料与方法
1.1 材料来源 马尾松毛虫资料来自安徽省潜山县森林病虫防治站,气象资料来自国家气象局,资料的时间跨度为1983—2014年,其中1998年数据缺失。
1.2 建模方法

1.2.2 列联表多因子多级综合预测法[11-14]列联表多因子多级综合预测法预报量等级的划分方法同1.2.1;预报因子的分级即自变量等级的划分,采用直线回归法。
2 结果与分析
2.1 利用马尔科夫链方法预测马尾松毛虫发生面积模型 将1983—2014年马尾松毛虫发生面积分级值相距1 a的各级值的转移概率记为P(1),相距2 a的记为P(2),相距3 a的记为P(3),逐个计算转移概率矩阵,越冬代(Y1)发生面积的转移概率矩阵如下:



计算得:P1=0.303 3,P2=0.376 3,P3=0.151,P4=0.17
可见P2最大,故预测2015年马尾松毛虫越冬代发生面积为2级,即1 467~3 133 hm2。同样可以预测2016年马尾松毛虫越冬代发生面积为2级,即1 467~3 133 hm2。2015年和2016年越冬代实际发生面积分别为2 333 hm2和2 400 hm2,两者较为吻合。
一代(Y2)发生面积的转移概率矩阵如下:



计算得:P1=0.547 3,P2=0.301 7,P3=0.023 7,P4=0.127
可见P1最大,故预测2015年马尾松毛虫一代发生面积为1级,即发生面积小于1 467 hm2。同样可以预测2016年马尾松毛虫一代发生面积为1级,即发生面积小于1 467 hm2。2015年和2016年一代实际发生面积分别为2 400 hm2和2 467 hm2,预测有一定的误差。
二代(Y3)发生面积的转移概率矩阵如下:



计算得:P1=0.25,P2=0.490 3,P3=0.5,P4=0.111
可见P2、P3数值相近且较大,故预测2015年马尾松毛虫二代发生面积为2级,即1 467~3 133 hm2。同样可以预测2016年马尾松毛虫二代发生面积为2级,即1 467~3 133 hm2。2015年和2016年二代实际发生面积分别为2 400 hm2和2 533 hm2,两者较为吻合。
2.2 利用列联表分析法进行马尾松毛虫发生面积的多因子多级预报 对越冬代(Y1)、一代(Y2)和二代(Y3)发生面积按极差法进行分级,并将其代入与其相关显著的自变量(xi)的直线回归式进行分级,将因子对Y1、Y2、Y3的条件概率列联表列于表1~3。

表1 各因子对Y1的条件概率列联表
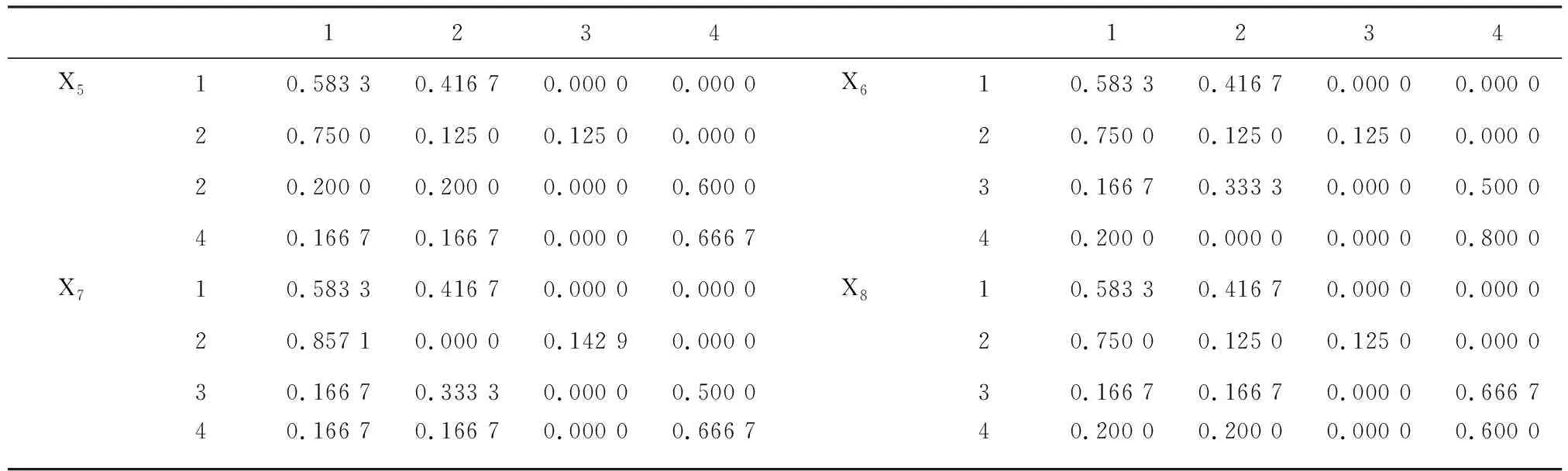
表2 各因子对Y2的条件概率列联表
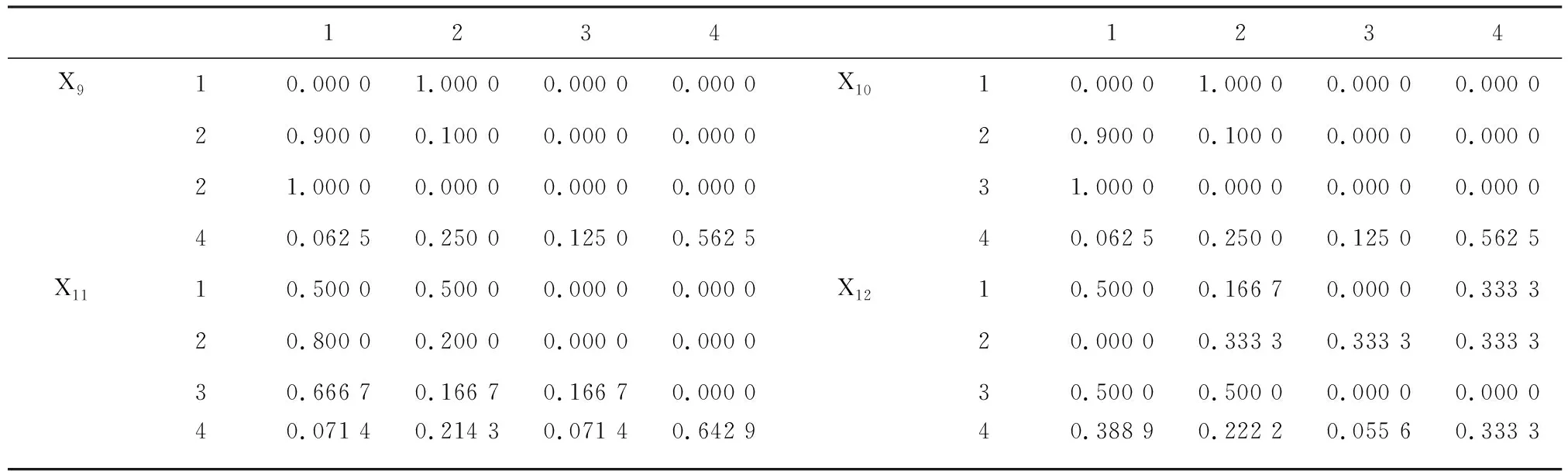
表3 各因子对Y3的条件概率列联表

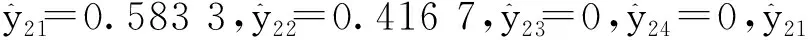

3 小结与讨论
利用马尔科夫链预测法和列联表多因子多级综合相关法建立安徽省潜山县1983—2014年马尾松毛虫越冬代、一代和二代发生面积预测模型,并用2015年和2016年马尾松毛虫各代发生面积进行验证。结果表明,马尔科夫链法预测结果误差较小,列联表多因子多级相关法预测存在一定误差,但与实际基本吻合。
马尔科夫链预报法要求害虫发生情况符合马尔科夫过程,通过运算求出状态转移概率,根据预报年的前1年,前2年和前3年的害虫发生级别分别查状态转移概率P(1)、P(2)和P(3),计算出可能出现级别的平均概率,用平均概率最大的那个状态作为预报年可能发生级别的预报值,预测结果比较准确。
列联表分析法要求必须具备系统的历年观察数据,用列联表法最重要的是如何划分等级,同样的资料用不同的标准分级,其预测效果相差悬殊,且每一个入选的自变量必须和因变量单相关关系达到相关水平方可,由于影响害虫发生因子常常是多个,利用多元回归计算时计算量大,且计算过程极易出现误差,与多元回归计算相比,利用列联表分析进行多因子多级预报法大大减少工作量,且预报比较准确。

