基于差速驱动的AGV驱动单元分析与改进设计

赵华东， 江 南， 雷超帆

(郑州大学 机械工程学院, 河南 郑州 450001)

0 引言

随着我国人工成本的逐渐升高，对产品质量，自动化、柔性生产的要求提高，商用自动导引车(AGV)[1]作为智能制造和柔性生产的关键环节，因其能实现高效、经济、灵活的无人化生产，广泛应用于工厂自动化生产线、仓储物流、机场和港口的物料传送[2-3].

近年来，国内外研究人员对AGV的结构和运动进行了大量的研究.王殿君等通过四轮差速原理，运用ADAMS软件分析了AGV转弯过程[4].刘国刚通过ANSYS仿真，对AGV车架进行了轻量化设计[5].夏田等通过建立AGV的静力学和动力学模型，采用Matlab/Simulink建立了仿真模型并仿真了一个驱动轮静止另一个转动的运动方式[6].刘治华等通过疲劳理论，采用ADAMS和NCODE分别对轨道车飞碟游乐设备的驱动轴进行了动力学和疲劳仿真分析，并得出驱动轴的寿命云图[7].

笔者以某公司设计的一款悬臂结构、链传动的AGV为例，研究驱动轮“外掰”和启停“冲击”的问题.该AGV的工况为：8小时工作制，用于轴承内外圈自动化生产线上将码垛完成后的轴承内外圈及托盘，转移到智能仓储的对应入口处，然后返回等待托盘再次装满，如此往复.其中轴承内外圈及托盘总重量为168 kg.AGV平均循环周期为42 min.工厂路面为环氧地坪漆.笔者通过反复试验和建模仿真分析的方法，确定了“外掰”及“冲击”的原因，提出了一种新的结构，且对新机构进行了校核.从结构应力，传动效率和精度上进行对比分析，验证了新机构的合理性.

1 问题分析

1.1 结构与现象描述

该AGV车身长600 mm，宽500 mm，高300 mm，为差速驱动、六轮布局形式，结构如图1所示.

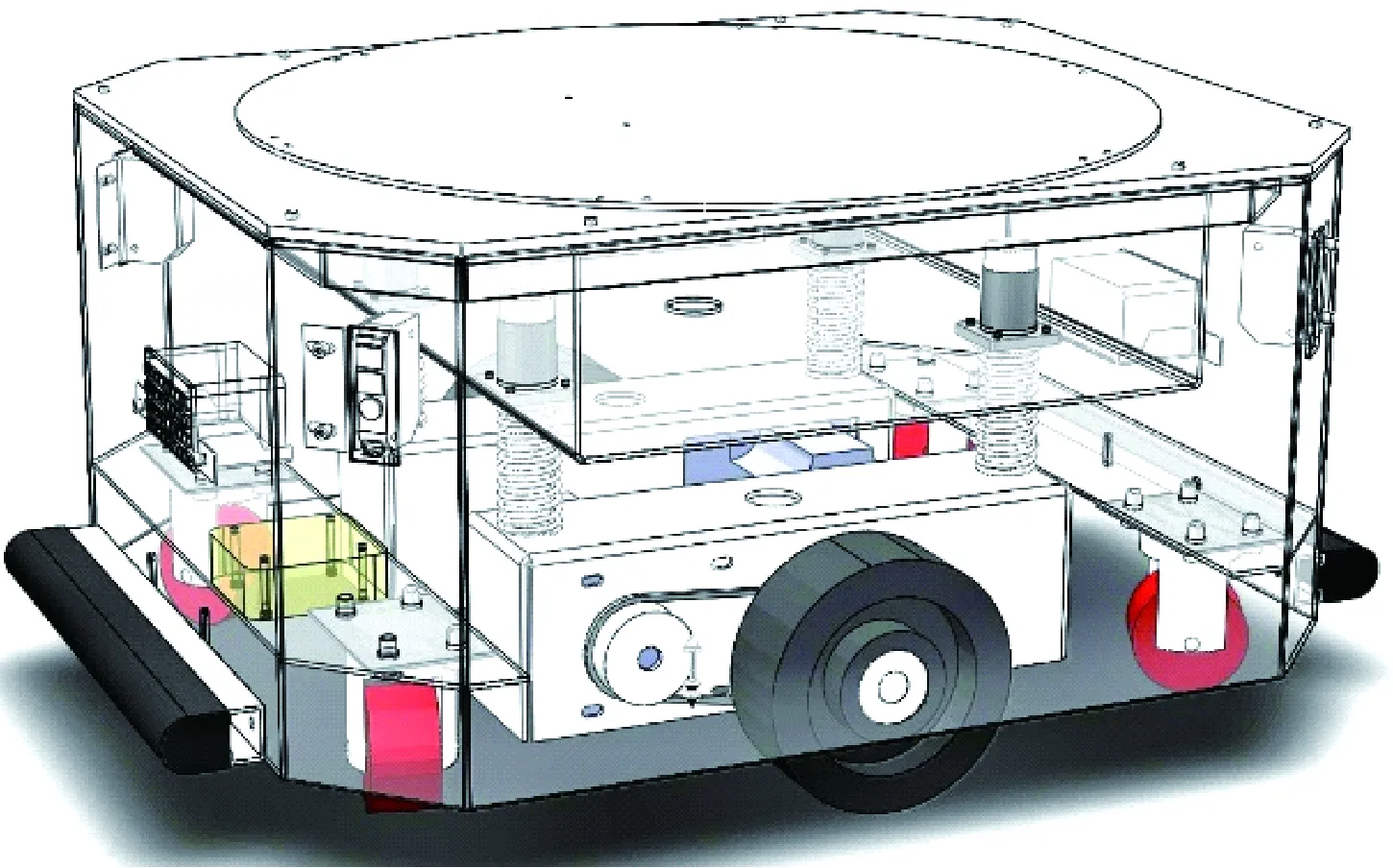
图1 AGV整体结构图Fig.1 The whole structure of AGV

小车车体总质量为57.15 kg，最大载重量为200 kg，驱动单元部分质量为24.34 kg，最大运行坡度5°，最大运行速度1 m/s，运行方向为双向.小车车身与从动轮直接连接，和驱动单元通过弹簧和导轨滑块连接在一起.这样驱动轮始终着地，防止因制造误差或地面不平坦导致打滑，造成小车运动失真，且有减震[8]的作用.

由于AGV小车壳体侧面板不可拆卸，故将AGV小车空载置于高于地面的平台上，在车轮外侧面与地面处固定一角尺作为参照标尺.然后在AGV车身上逐渐加载200 kg重物，通过观察车轮外侧面与角尺间的间隙变化进行试验.观察到满载时，驱动轮与地面接触处因受力而向外倾斜，即驱动轮“外掰”，如图2所示.

图2 “外掰”现象示意图Fig.2 Sketch of the phenomenon of “outside breaking”

试验时将AGV断电侧翻放置，用较小力拨动驱动轮时，车轮在一定的范围内转动，但驱动电机并未产生相应转动，而是链轮轮齿在链节距的空隙中晃动.在AGV启停时会出现因机构空隙产生的明显冲击，即启停“冲击”.针对上述现象，分别从结构受力和传动机构特点进行分析，找出导致该现象的原因，并提出了新的驱动单元机构.

1.2 静力分析

1.2.1 静应力预测

由材料力学知识可知：AGV驱动单元是一个“L”形的悬臂结构,如图3所示，将在接触点A处、B处和C处形成较大的应力集中[9]. 为进一步确定应力较大的区域，现进行有限元分析.

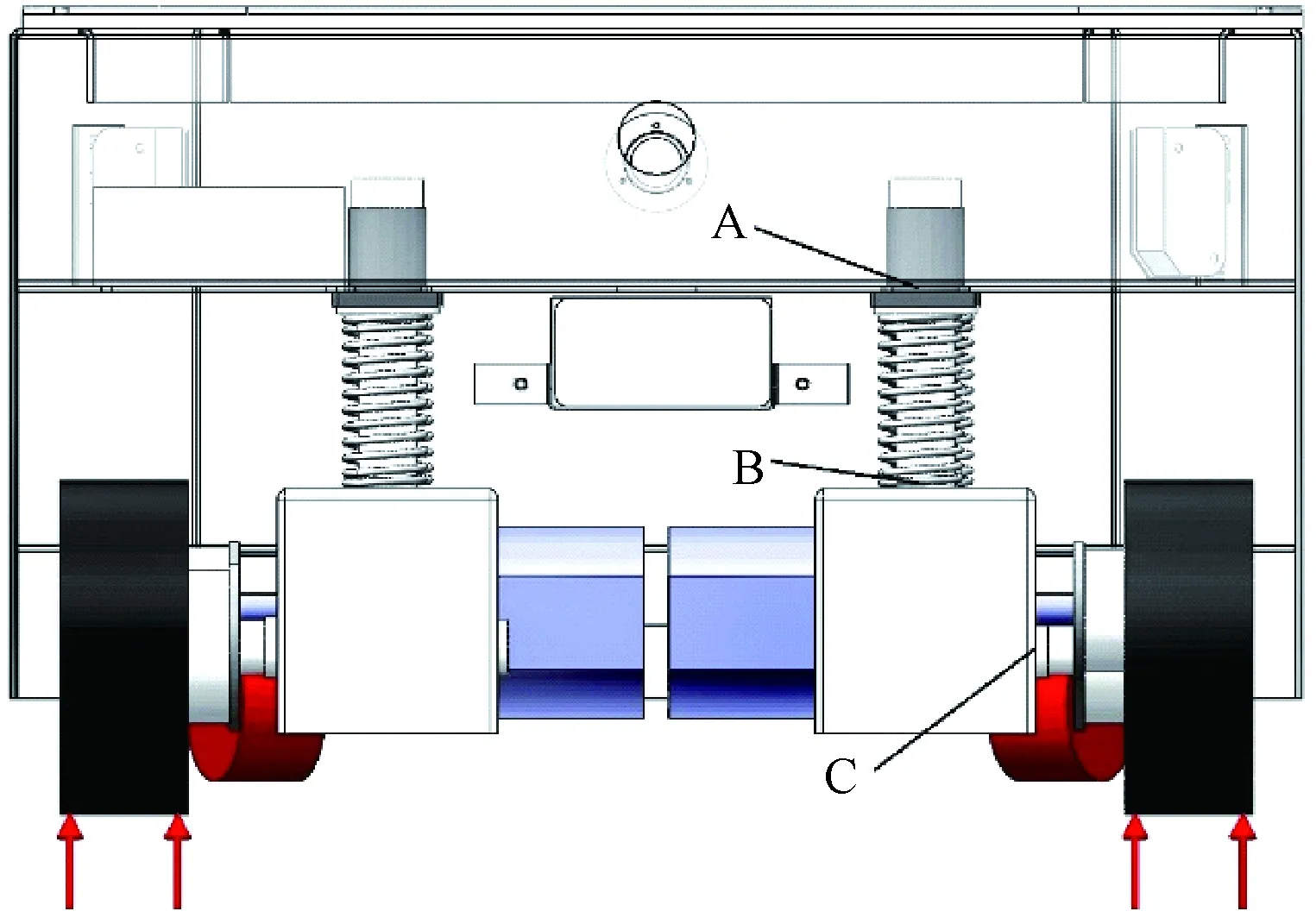
图3 驱动单元受力示意图Fig.3 Force diagram of driving unit

1.2.2 有限元分析

(1)简化模型和定义材料.本机构用SolidWorks Simulation进行有限元仿真分析[10-11].为保证结果可靠，将模型中不影响受力的部分进行简化，只保留驱动轮轮轴、驱动单元壳体、圆柱导轨和与之接触的壳体进行有限元分析.材料的弹性模量为210 GPa、密度为7 800 kg/m3、屈服强度为220 MPa，选择普通碳钢材料.

(2)设定边界条件.小车重力完全施加在驱动单元上，故为分离出的驱动单元添加平面约束，使其只能沿竖直方向运动.添加弹性支撑代替车轮.与直线轴承相接触的直线导轨添加“接触”约束.动力壳体与直线轴承之间的弹簧用“弹簧”来代替.效果如图4(a)所示.

(3)添加载荷.满载时驱动单元上的等效质量为232.81 kg，重力加速度取9.806 65 m/s2.室内平地上运动，选择载荷系数为1.2.载物台上重物放置区内施加载荷2 739.7 N.车轮与地面接触的摩擦系数选为0.25.先利用无摩擦仿真得出接触面正压力，再在接触面添加等效摩擦力342.5 N.

(4)划分单元格.SolidWorks Simulation为保证对各种几何体和面的网格划分的通用性，统一采用一阶四面体、二阶四面体、一阶三角形、二阶三角形进行网格划分，且大量试验保证了算法的可靠性和效率.对于非压力容器的薄板件，在进行网格划分时推荐使用单层二阶四面体进行网格划分结果更优[12-13].故本仿真统一采用二阶实体四面体进行板件和实体的网格划分.

总体采用基于曲率的网格，雅可比点数为4点，调整好单元格的精度进行网格划分[14]，未细化区域最大单元格为28.545 5 mm，最小单元格为5.709 1 mm，增长比率为1.6.

对关注的区域进行单元格的细化.选取应力集中区的零件和边界线：直线轴承、驱动轮轴、动力单元壳体、导轨和动力壳体边线，使用网格控制进行网格划分.

细化部分最大网格为5.119 26 mm，最小网格为3.358 93 mm.网格节总数为946 585，单元总数为644 846.驱动单元模型网格划分，如图4(b)所示.

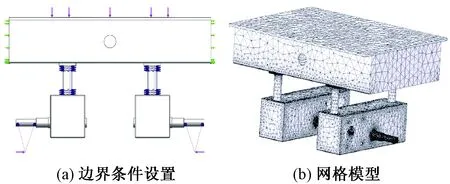
图4 边界条件和网格模型Fig.4 Boundary conditions and grid model

(5)进行有限元分析.运行有限元解算器进行解算，得出等效应力分布云图，如图5所示.

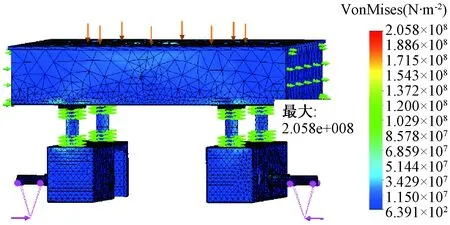
图5 原系统等效应力分布图Fig.5 Equivalent stress distribution diagram

1.2.3 结果分析

利用Simulation的设计洞察功能以颜色着重显示出应力较大的区域，如图6所示.

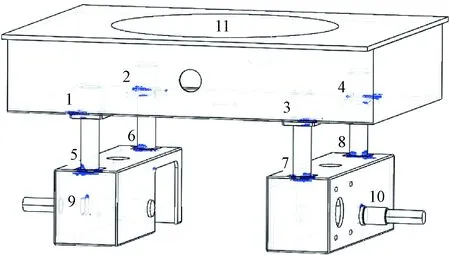
图6 应力较大区域Fig.6 Larger stress area

从图6中可以看到，标号1～10处是应力较大区域，11代表上壳体.其平均应力、最大应力、均方根值见图7.最大应力出现在4处，为205.8 MPa，而材料的屈服强度为220.6 MPa，安全系数仅为1.07.一般车辆设计要求重要部位的安全系数大于等于2.

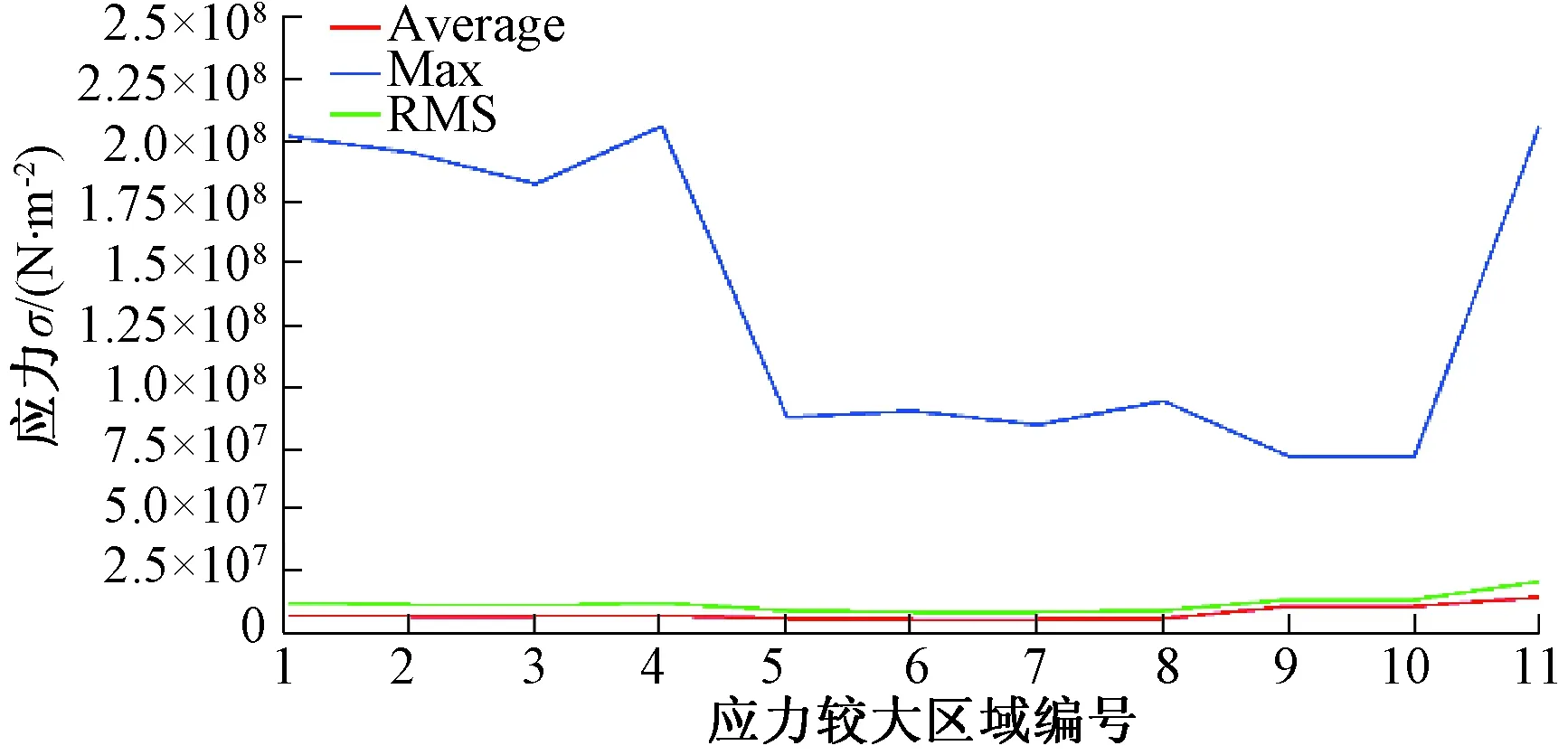
图7 原系统应力较大区域数据图Fig.7 Large stress area data diagram

驱动单元“L”形悬臂结构引起了过大局部应力，同时，这样的结构会将车体接触处的各个间隙进一步放大，使车轮的“外掰”现象更加明显.

1.3 传动结构分析

在AGV启停时，有明显的因机构间隙引起的位移，即“空隙冲击”现象，将影响AGV的运动精度.AGV底部实物结构如图8所示.

图8 AGV底部实物结构图Fig.8 Physical bottom structure of AGV

AGV的驱动电机与驱动轮之间靠链传动连接，而链传动在有双向运动时会引起较大的冲击.在非连续运动时，没有二次定位机构的辅助，常常会有“蹿动”，丢失精度.

2 新型驱动单元结构设计

2.1 AGV驱动单元设计

2.1.1 方案设计

针对AGV运行中遇到的上述问题，新的机构需要避免车轮的长悬臂和链传动，同时考虑两个驱动轮的间距与干涉，以及成本问题，并要求能对应力状况、可靠性有所改善.

将驱动轮轴由悬臂梁结构改为简支梁的形式，驱动轮轴两端通过轴承与驱动壳体连接在一起.同时，将原有电机改为弧锥直角式中空减速电机，使电机和驱动轮轴直接相连.该连接方式将避免因悬臂结构产生的弯矩，同时省去中间的链传动环节，传动精度、传动效率都有所提高.

2.1.2 选型设计

AGV运动时沿运动方向上所受的加速度阻力、斜坡阻力、风阻、滚动摩擦阻力和静摩擦提供的驱动力满足方程[15]：

Fk=Fa+FG+FR+FD，

(1)

(2)

FG=mg sinα，

(3)

(4)

式中：Fk为静摩擦提供的驱动力；Fa为等效加速度阻力；FG为坡度阻力；FR为车轮滚动摩擦阻力；FD为空气阻力；δ为旋转质量的换算系数；m为车体和货物总质量；V为速度；t为时间;α为坡度角，当坡度角较小时有sinα=α；CD为风阻系数；ρa是空气密度，为1.225 8 kg/m3；A为迎风面积.

对小车单个驱动单元的驱动轮进行受力分析可得方程：

FkRK=MK，

(5)

FR=fRG，

(6)

式中：Rk为车轮半径；MK为车轮上驱动力矩；FR为车轮滚动摩擦阻力；fR为滚动摩擦系数；G为单个驱动轮上承受的车体和重物的总重力.

通过上式的受力分析，计算出驱动力矩、额定转速、减速比和各传动件、连接件电机参数.通过对设计寿命和传动精度及最大扭矩的要求，计算选择了轴承、键、轴和一些连接件的相应型号[16].

2.2 新型驱动单元模型建立

根据设计的加工件和选用的标准件尺寸，建立AGV驱动单元的三维模型.其结构如图9所示.

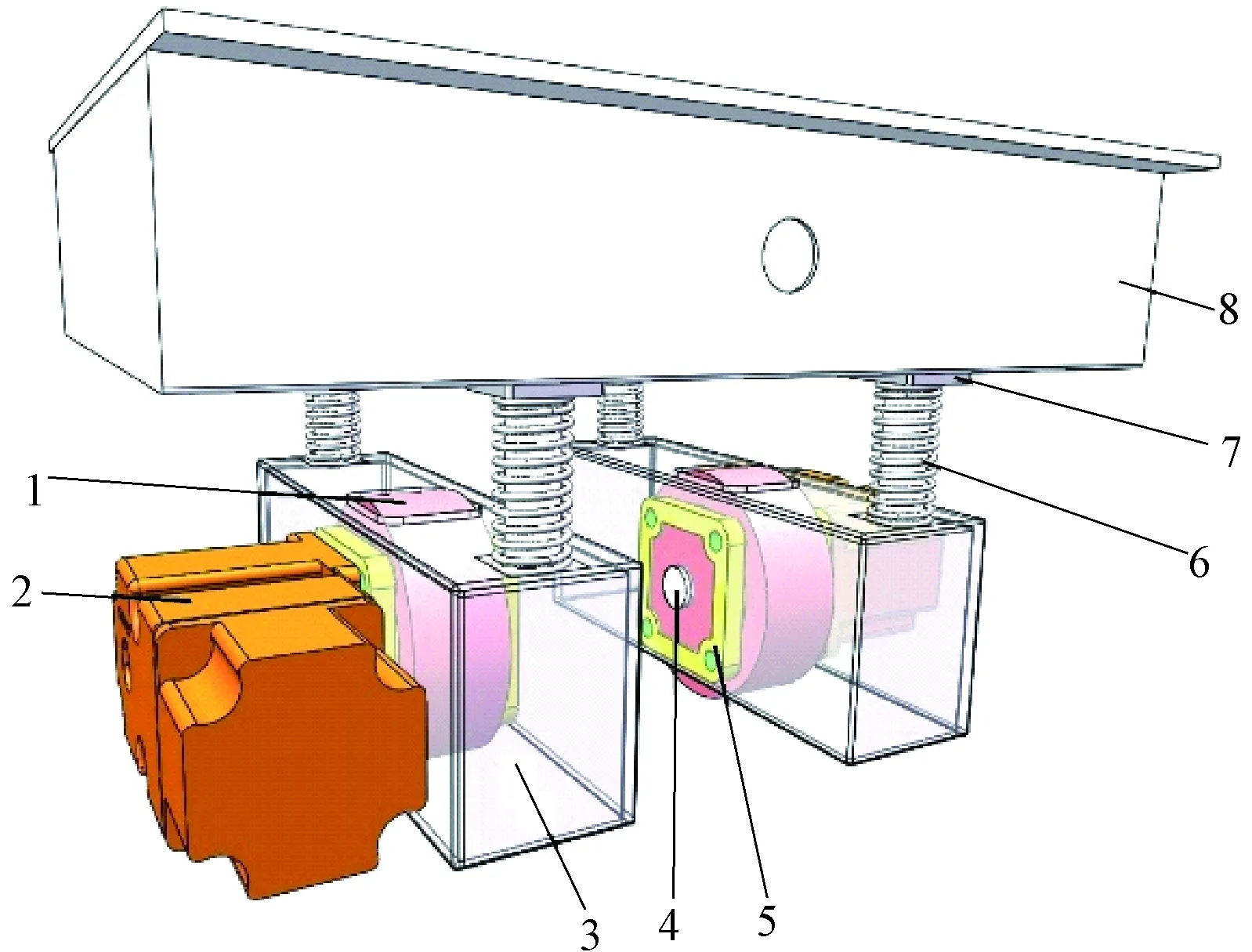
1—驱动轮;2—驱动电机;3—驱动壳体;4—驱动轮轴;5—法兰轴承;6—弹簧;7—直线轴承;8—车身上壳体图9 新型动力单元结构图Fig.9 Structure of new type of power unit

驱动单元使用简支梁式直连驱动电机的形式有效避免了驱动单元的整体弯矩，降低了材料应力，进而避免了满载运行时车轮大幅“外掰”问题.由于电机的安装孔可以调节，电机直连的方式并没有让电机承受来自径向的压力，而且这种连接方式提高了传动的精度和可靠度.

3 驱动单元对比分析

3.1 应力分析对比

为深入研究新机构的应力，现对新驱动单元进行有限元分析.①模型简化和材料定义与原驱动单元相同.②设定边界条件时，代替车轮的弹性支撑按车轮实际接触位置添加，其他设置和原驱动单元相同.③添加载荷，设置和原驱动单元相同.④划分单元格.细化零件按推荐良好品质设置，最大网格为5.284 38 mm，最小网格为3.390 31 mm.划分网格后，节总数为924 859，单元总数为627 313，如图10所示.⑤运行解算得到仿真结果如图11所示.应力较大区域数据如图12所示. 改进前后应力较大区域数据对比如图13所示.

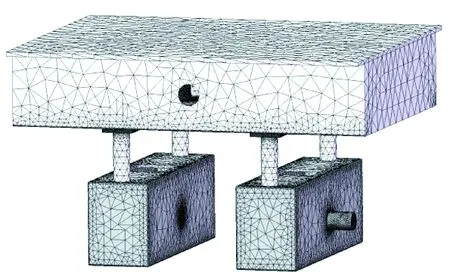
图10 驱动单元网格模型Fig.10 The mesh model of driving unit

图11 改进系统等效应力分布图Fig.11 Equivalent stress distribution diagram

图12 改进系统应力较大区域数据图Fig.12 Large stress area data diagram

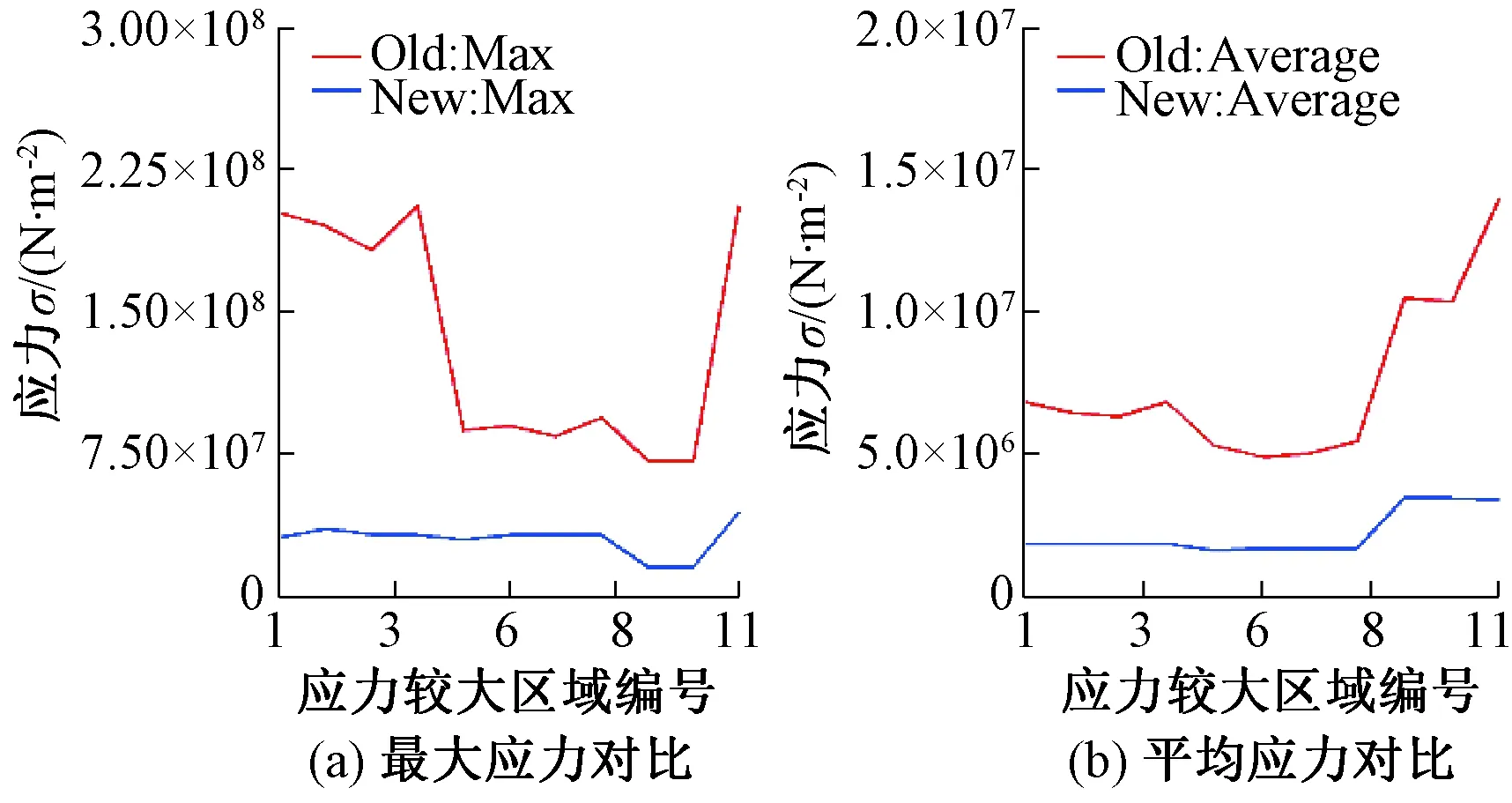
图13 应力较大区域数据对比图Fig.13 Large stress area data comparison diagram

由AGV新型驱动单元的结构模型等效应力分布云图和应力较大区域对比图可以看到，在材料、尺寸、分析条件一样的情况下，新的驱动单元最大的应力出现在3号区域附近，为44.57 MPa，远远小于原有驱动单元的最大应力205.8 MPa，同时也远远小于材料的屈服强度220.6 MPa.此时，新机构的安全系数大大增加，为4.95，满足安全系数大于等于2的要求.改进后应力集中区域最大应力值和平均应力值都有明显下降.其他条件不变时，结构的变化使最大应力降低为原来的21.66%，这为AGV车体的轻量化设计提供了较大空间.

3.2 精度分析对比

在新的驱动单元中，避免使用大间隙传动机构滚子链的使用，使用弧锥直角空输出轴减速电机与驱动轮直接相连.在减速器上选用弧锥直角空输出轴的减速器，使连接的空间减小，方便两个驱动单元单体间距调整.经计算选型的弧锥直角减速电机的减速比为5，传动级数为2级，较少的传动环节和较低的传动级数能有效地减小传动中由各机构接触间隙形成的误差.其结构如图14所示.

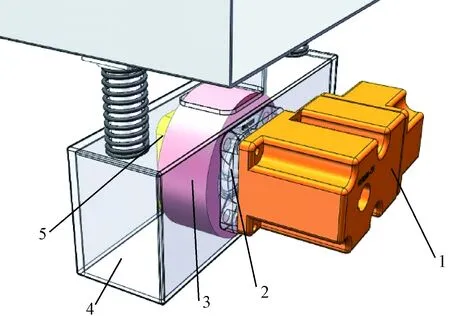
1—弧锥直角空输出轴减速电机; 2—驱动轮轴; 3—驱动轮; 4—驱动壳体; 5—法兰轴承图14 新型动力单元单侧结构图Fig.14 New power unit unilateral structure

与原来驱动单元相比，新驱动单元消除了“空隙冲击”现象，同时减少了中间传动的环节，消除了中间环节的误差，同时减少了误差积累，使传动的精度大大提高.

4 结论

新驱动单元在受力上，避免了“外掰”问题，使最大应力降低了78.34%，机构安全系数提升了4.63倍；改进了传动机构，降低了传动级数，减小了传动间隙，提高了传动系统的精度；在制造成本上，减少了机加工量，提高了机构可靠性，降低了设计加工成本和维护更换成本.结果表明，新型驱动单元解决了传统驱动单元车轮“外掰”和传动机构“大空隙”问题，为AGV驱动单元的设计提供了一种方便、可靠的结构.