菌群优化方法及其应用研究综述

晏晓辉， 朱云龙， 张智聪， 吕赐兴， 李 帅， 蚁文洁

(1.东莞理工学院 机械工程学院，广东 东莞 523808； 2.东莞理工学院 电子工程与智能化学院，广东 东莞 523808； 3.深圳大学 管理学院,广东 深圳 518060)

0 引言

群体智能(swarm intelligence, SI)算法是近年来智能计算和优化领域的热门方向.自20世纪90年代起，学者们从蚁群觅食、鸟类飞行、蜂群分工合作、萤火虫发光吸引、鱼群结伴游弋等行为中受到启发，先后提出多种群体智能算法[1-5]，并在许多数值优化和工程优化问题上进行了测试应用.对于传统运筹学方法难以求解的大规模组合优化问题，群体智能算法能在较短时间内求得较好的满意解，展现出极大的优越性.

菌群优化是基于细菌群体的优化行为而提出的一类新型群体智能方法.早在20世纪中期，生物学家就通过显微镜观察到细菌的移动并非随意，而是具有一定的规律.1960年，Alder深入研究了大肠杆菌的分子机制，提出了细菌的趋化性机理.1974年，Bremermann在文献中指出了细菌趋化行为用于优化的可能性[6].1990年Bremermann根据细菌内部的反应机制以及细菌与环境的相互作用机制提出了细菌趋化优化模型，并将其用于神经网络训练[7].随后，许多学者对细菌行为用于优化展开了研究，其中比较成功的细菌优化算法有细菌趋化算法(bacterial chemotaxis algorithm, BC)[8]、细菌觅食算法(bacterial foraging optimization, BFO)[9]和近年来提出的磁性细菌算法(magnetotactic bacteria optimization algorithm, MBOA)[10]，而基于这些算法的改进和应用研究也一直未曾间断.

以最有代表性的BFO算法为例，2000—2017年，在Web of Science数据库以“bacterial foraging optimization”为关键词可搜索到学术文献781篇(数据截至2017年9月28日)，每年的文献数量如图1所示.由图1可以看出，相关研究热度一直稳步攀升.从文献的国度来看，主要集中在中国、印度、美国、英国和伊朗，如图2所示.

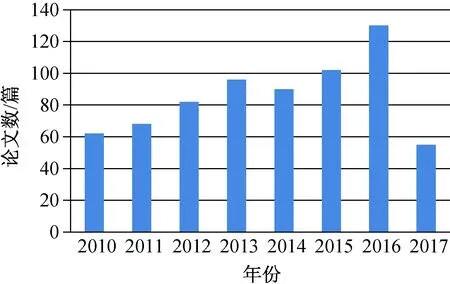
图1 历年BFO算法相关文献数量Fig.1 Quantityof literatures relevant to BFO algorithm in past few years

图2 细菌觅食算法相关研究国家分布Fig.2 National distributingsituation of literatures relevant to BFO algorithm

与粒子群算法等成熟群体智能算法相比，基于菌群的优化研究还处在初步阶段.基本BFO算法的优化能力也与标准PSO算法有一定差距.然而，与鸟群、鱼群等其他生物群体相比，细菌个体结构和行为简单，但群体种类及特性多变，不同菌群之间的相互关系多样且复杂，符合智能涌现的非线性、多样性要求.在多层次群体建模上可能更具优势.此外，菌群快节奏的生命演化周期也适合优化模拟，值得进一步深入研究.目前，国内外关于菌群优化的综述文章较少，武林娟、高金凤的两篇综述文章[11-12]均从算法理论、算法改进、算法混合、算法应用4个方面进行了综述，但分析较少，缺乏系统性.李娜等对细菌觅食算法的进展进行了回顾，但应用部分的综述较为简单，改进建议也仅从改进算法现有的3个操作着手[13].外文文献也仅有几篇关于BFO算法的综述：其中1篇为Hernandez等在2013年CEC会议上的论文，集中讨论BFO算法在约束数值优化上的应用[14]；另外2篇为牛奔等在2010年ICIC国际会议上的论文[15-16]，分别对BFO算法从背景、发展、应用和挑战4方面进行了综述.从图1可以看出，近年来关于菌群优化的研究也有大幅增长，因此，笔者拟对近几年的菌群优化研究内容和发展方向进行系统的梳理，以期为本领域的学者提供一个更为清晰的思路.

基于781篇文献的标题，笔者对其进行了词频分析，去掉介词以及“bacteria”“foraging”“optimization”“algorithm”等与BFO直接相关的单词，再用高词频词汇与“bacterial foraging optimization”做主题组合查询，文献数量排序如图3所示.

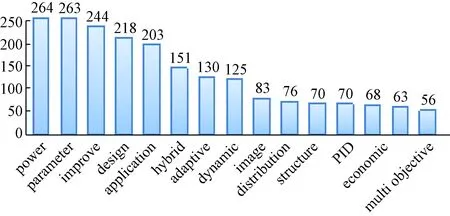
图3 相关文献高频关键词Fig.3 High frequency key words in relevantliteratures

从关键词组合的主题文献数量来看，文献的研究点主要集中在算法改进和应用上.而诸如“power”“parameter”“hybrid”“adaptive”“dynamic”“image”“structure”“PID”“economic”“multi objective”“operator”等关键词也表明了算法改进和应用的主要方向和场景.下文将从基本菌群优化方法、菌群优化方法改进研究和菌群优化方法应用研究3个方面展开综述，进而探讨菌群优化方法的发展方向.

1 基本菌群优化方法

1.1 BC

细菌趋化算法BC的早期研究是基于Berg、Brown和Dahlquist提出的细菌趋药性微观模型.在此基础上，S. D. Müller等人结合最新研究，提出了BC算法[8].实际上，BC算法并非基于细菌群体，而是基于对细菌单个个体运动觅食行为的模拟.细菌不断地感受它周围的环境变化并利用它过去的经验和当前状态来调节下一步行动策略，从而寻找最优点.在BC算法中，细菌对引诱剂的反应运动遵守如下的假设：①细菌的运动轨迹是由一系列连续的直线组成，并且由运动方向和移动距离两个参数决定；②细菌在进行下一步运动要改变运动方向时，向左转和向右转的概率相同；③细菌在各段相邻轨迹间的夹角由概率分布来决定.

BC算法在迭代过程中，细菌仅利用它上一步或上几步的位置信息来确定下一步的移动，其实质是一种近似梯度的随机搜索方法.

1.2 BFO

2002年，模拟细菌群体的觅食和繁殖行为，Passino提出了细菌觅食优化算法BFO[9].算法从初始化一组随机解开始，将细菌的位置表示为问题的潜在解，通过模拟菌群的趋化(chemotaxis)、繁殖(reproduction)和迁徙(elimination-dispersal)行为来改变细菌的位置，从而进行优化.

原始BFO算法的结构为3层循环嵌套结构.主要参数包括：迁移次数Ned、繁殖次数Nre、趋化次数Nc，分别控制迁徙、繁殖和趋化的次数.此外，还有种群规模S、迁移概率Ped、最大前进次数Ns等.

趋化操作是BFO算法的核心层.在趋化环节，细菌个体按照如下公式来更新其位置，

θi(j+1,k,l)=θi(j,k,l)+C(i)φ(j)；

(1)

(2)

式中：θi(j,k,l)代表第i个细菌个体在第l次迁徙、第k次繁殖、第j次趋化中的位置；C(i)代表细菌个体i的趋化步长；φ(j)为第j次趋化中随机生成的趋化方向，为一单位向量，如公式(2).当细菌通过上述公式，位置得到改善时(如函数适应度变优)，细菌个体可以按照上述公式继续前进一步，直到位置变差或达到最大前进次数Ns.趋化操作可以实现细菌向更为有利的生存环境移动，获得较优的位置.

每进行Nc次趋化操作，就进行一次繁殖操作.根据在这一轮趋化中的适应度总和来进行排序，适应度总和较高的一半个体被认为是获得了充足的营养，在原位置进行分裂复制；另一半个体执行消亡操作，从种群中移除.繁殖操作通过优胜劣汰，来加快收敛.

每进行Nre次繁殖操作，就进行一次迁徙操作.所有细菌个体以概率Ped进行迁徙，被移到解空间中一随机位置.迁移操作可以在一定程度上避免算法陷入局部最优，以免早熟.

Ned次迁徙操作完成后，算法结束，输出最优解.

此外，BFO算法还模拟了细菌的群聚行为.菌群觅食过程中，每个细菌个体除按照自己的方式搜索食物外，还会收到其他个体发出的引力信号，若是吸引力信号，则个体会游向种群中心；若是排斥力信号，则保持个体与个体之间的安全距离.细菌间聚集作用的数学表达式如公式(3)所示，

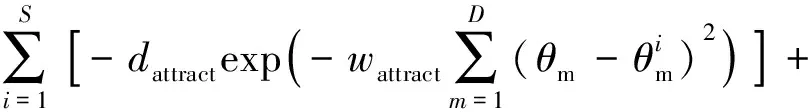
(3)

1.3 MBOA

磁性细菌优化算法(magnetotactic bacteria optimization algorithm, MBOA)是哈尔滨工业大学莫宏伟等根据细菌的趋磁性提出的一种优化方法[10].磁性细菌是对地球磁场和外部磁场敏感，可以沿着磁力线方向和氧气浓度梯度方向运动的一类特殊细菌的总称.该趋磁现象最早由生物学家Blakemore于1975年发现[17].经研究，这类细菌具有趋磁性的原因是其体内存在磁小体.磁小体的主要成分为磁铁矿(Fe3O4等)，呈细小颗粒状被包裹在蛋白膜中.该类细菌通常包含多个磁小体组成的磁小体链，因而整个细菌类似于生物磁针，能感应磁力线并通过鞭毛摆动沿其方向运动.此外，磁小体链还能起到利于细菌能量收集、调剂胞内氧化还原数值大小等作用.关于磁性细菌的研究在文献[18]中有详细论述，在此不作过多介绍.2013年，莫宏伟教授根据磁性细菌的特征提出了MBOA算法.在MBOA中，将每个具有磁小体的细菌看作解空间中的一个解.其求解过程为磁小体调整适应磁场的过程，而最终具有最小净磁能的磁小体即为所求的最优解.算法首先初始化，在求解空间内随机生成一系列磁小体个体；其后，根据细胞间的相互作用计算磁小体力矩；接着，对磁小体实施拓展操作以获得新的力矩；然后，对磁小体的力矩进行调整替换，重复上述计算、拓展和调整过程直到算法满足结束条件.

在原始MBOA的基础上，莫宏伟团队及其他学者对MBOA进行了一系列研究，提出了基于最优个体指导的MBOA算法[19]、基于力矩迁移的MBOA算法[20]、趋磁性细菌多目标算法[21]等，并将这些算法应用于多峰优化、约束优化等数值优化问题以及移动机器人路径规划等工程问题[22-23].

2 菌群优化方法改进研究

结合上述菌群优化的关键词分析和其相关性，笔者将从参数与结构改进、多算法混合改进、算子改进和多目标优化改造等4个典型方面展开菌群优化方法改进研究综述.需要说明的是，同一篇文献也可能综合用到下面的多种改进方法.

2.1 参数与结构改进

参数改进是群体智能算法改进的常见方式[24].与粒子群算法、遗传算法等经典算法相比，原始BFO算法有Ned、Nre、Nc、Ped、Ns、C(i)等主要参数，聚集操作中还有4个参数，参数个数较多，不便于控制.

BFO算法参数较多的原因之一是采用了3层循环嵌套结构.如果Ned、Nre、Nc等参数设置不当，可能在不合适的时间进行繁殖、消亡与迁徙等操作，从而影响算法的收敛性.在一些改进的菌群优化算法中，去掉了趋化-繁殖-迁徙3层嵌套，将繁殖和迁徙作为趋化的并行步骤来进行[25].基于该算法结构的改进算法可以去掉Ned、Nre、Nc等参数.

BFO算法中另外一个重点参数改进为趋化步长C(i).现有的群体智能算法都是通过种群的进化迭代来实现最优解的改进.进化迭代在算法执行的过程中表现为种群中各个体在解空间中的位置更新.不同算法基于所模拟的不同生物行为，其具体更新公式各不相同.其中，主要包括两大类：基于相对位置的更新和基于绝对位置的更新，表1为几种典型群体智能算法的更新公式.

表1 典型算法位置更新公式比较Tab.1 Comparison of position updating equation to several classic algorithms

由表1可以看出，GA、PSO、ABC等算法都采用的是基于相对位置的更新，通过个体之间的组合或差异来产生新的个体.原始的BFO和FA算法中采用了基于绝对位置的更新.BFO算法中，细菌个体在确定游动角度后，沿该角度以步长C(i)向前游动.FA算法中，随机项α(rand-0.5)是以一个常数α乘以一个(-0.5，0.5)的随机数[26].在基于相对位置的更新中，种群中的个体的前期差异大，算法趋向于全局搜索，后期差异小，算法趋向于局部开发，能动态地平衡算法的多样性和收敛性.在基于绝对位置的更新中，个体更新中使用指定的步长.该类方法在局部搜索上有一定的优势，但若步长设置不当，在前期可能搜索的范围不够，后期难以收敛,文献[27]的研究证实了这一点.为弥补上述菌群优化中基于绝对位置更新带来的缺点，很多学者对趋化步长C(i)进行了改进.其中，大部分学者采用了基于动态下降或自适应的步长.

作者在前期的研究中，抛弃了趋化-繁殖-迁徙3层嵌套，改为对细菌的生命周期进行建模，根据细菌个体在优化过程中的营养获取和流失动态地进行分裂、死亡和迁徙，并在趋化步长线性下降的基础上根据营养值动态地改变其步长，取得了较好的效果[27].牛奔等提出了(structure-redesign-based bacterial foraging optimization, SRBFO)算法，将原始的BFO算法中3层嵌套改为单层循环，并重新设计了繁殖、消亡和迁徙操作，进一步简化算法的结构，在投资组合优化的实验中证明了该算法优于PSO算法[28].Tan等提出了一种自适应结构重构的细菌觅食算法(adaptive structure-redesigned-based bacterial foraging optimization, ASRBFO)，在ASRBFO中，采用自适应的趋化步长，用个体的当前位置、历史最优位置、所有细菌的平均位置等信息来计算细菌的趋化步长.通过该方法，算法收敛速度和精度优于其他对比算法[29].在对BFO改进的研究中，大多数文献都有涉及对趋化步长的改进.

2.2 多算法混合改进

与其他优秀算法的思想或算子结合也是算法改进的一大途径.自菌群算法提出以来，许多学者在这方面展开了研究.

Manikandan等针对不同蛋白质序列分析中多目标多序列对比带来的计算量大的问题，将BFO算法和GA算法结合，提出一种BFO-GA算法来实现高效比对.实验结果表明，该算法优于多种传统的序列对比算法以及ABC、PSO等经典智能算法[30].Chen等结合BFO算法和PSO算法提出一种BFPSO算法，用于神经模糊分类器的参数优化[31].该算法在局部搜索中采用BFO的趋化操作，在全局搜索中采用PSO的搜索方法，取得了较好的效果.Emre等将BFO算法中的趋化操作与差分进化算法(differential evolution, DE)结合，提出一种趋化差分优化算法，在CEC2014测试集上的测试结果表明，该算法优于原始的BFO算法[32].杜鹏桢等提出一种混合蜂群算法的自适应细菌觅食算法.在该算法中，借鉴人工蜂群算法的雇佣蜂行为，设计出一种雇佣蜂趋化算子.此外，在原趋化的基础上提出自适应步长趋化算子.算法根据种群的多样性在两种趋化算子中进行自适应切换[33].Manjith将BFO算法和改进的布谷鸟搜索算法(cuckoo search, CS)结合，用于解决认知无线电的频道估计误差最小化问题.测试结果表明，该算法得到的导频序列优于其他算法[34].Wu等提出一种BF-PSO-FSVCM模型，将BFO和PSO算法结合，用于优化模糊支持向量机的未知参数，从而提高分类器的精度，更好地鉴别肌电图信号的疲劳状态[35].

在算法混合的研究中，与遗传算法和粒子群算法的混合居多.其他一些新兴智能算法也有涉及.在算法混合中经常利用BFO算法的框架或趋化算子.趋化算子“改进则继续试探一次”的思想可以较好地调整计算资源的分配，在潜在的最优解附近加强局部搜索.

2.3 算子改进

BFO算法的核心是趋化操作[36].因此算子改进最多的是趋化算子的改进.在2.1节中已经提到一些关于趋化步长的改进.此外，还有一些研究是针对趋化算子中的翻转方向或新个体生成公式的改进.

Yang等提出了一种BFOCC算法.该算法采用了新的趋化算子：每个细菌随机选择一个标准基向量作为趋化方向来游动或翻转，从而减少各维度之间的相互干扰.另外，该算法还引入了一个新设计的共轭算子来加强细菌之前的信息交换，提高算法的收敛性[37].Meng等在BFO的趋化操作中引入了变异因子，在每次迭代中，细菌个体以一定概率被选择并进行变异.经测试，采用小波变异的方法效果最为理想.该改进的算法被用于阵列综合问题[38].Hernandez等提出了一种改进的菌群优化算法用于四杆机构的综合优化.该改进的菌群优化算法在趋化操作中引入了两种游动算子.其中，一种倾向于全局搜索，另一种则加强在细菌个体附近的邻域搜索.通过这两种游动因子，细菌在搜索过程中能找到更好的解[39].Zhao等在趋化操作中引入混沌搜索算子来增强细菌个体的活跃水平，拓展其搜索空间，用以解决置换流水线调度优化问题[40].

除趋化算子外，也有一些学者对细菌觅食算法的繁殖、迁徙等其他算子进行改进.

Svrakov对BFO算法的繁殖算子进行了分析，将繁殖算子与进化算法的选择进行了类比.分析表明，一个稳定的繁殖活动有助于细菌的快速收敛[41].Mai等对BFO算法中的消亡-迁徙操作进行了改进，引入了一个自适应的迁徙概率，根据细菌个体的适应度来确定其是否迁徙.算法还在趋化移动后加入了一个PSO算法的学习算子.实验表明改进后的算法具有更好的收敛速度和收敛精度[42].Liu等针对BFO算法中迁徙操作随机性太强这一缺点，引入了信息素来控制细菌的迁徙.此外，在繁殖算子中加入了柯西变异来增强算法的全局搜索能力.测试结果表明，该算法能提高收敛速度，并避免陷入局部最优[43].

2.4 多目标优化改造

经典群体智能算法提出之初大多用于单目标优化问题.对其进行改造使之能适用于多目标优化问题也是算法改进的一大方向.

Tan等人提出一种基于全面学习策略的多目标细菌觅食算法，用于电力系统分配的多目标优化.算法通过非支配排序和拥挤距离来保持非支配解集的多样性.此外，算法还采用了全面学习策略来增强BFO的搜索能力，并在繁殖操作中采用了基于健康值排序的方法来提高菌群的质量[44].Zhou等建立了抽水蓄能水电站的导叶关闭计划优化模型.该模型综合考虑单位转速的上升速度,每个液压单元特定节点的压力以及各种复杂的液压和机械约束等多个优化目标，采用了一种增强的细菌觅食优化-重力搜索算法来对其进行求解.该算法采用了种群重建、自适应的选择趋化算子及局部搜索策略，并使用外部存档来保存精英解集，较好地解决了优化问题[45].

多序列对比问题(multiple sequence alignment, MSA)是计算生物学和生物信息学中经常遇到的一类多目标优化问题.Rani等提出多目标细菌觅食算法(multi-objective bacterial foraging optimization, MO-BFO)对其进行求解.测试结果表明，该多目标细菌觅食算法优于其他对比算法[46].牛奔等人提出一种多目标菌群优化算法，该方法综合采用健康值排序和帕累托支配机制来实现多目标优化.此外，通过一定概率保留边界非可行解来保持种群的多样性.算法通过多样性和总逼近距离来评估非支配前沿的优劣，结果表明了该算法的有效性[47].在另一种多目标菌群优化算法中，牛奔等还将邻域搜索引入到多目标细菌优化算法中，采用基于环形拓扑和星形拓扑的两种邻域搜索来提高非支配前沿的精度和多样性[48].Yi等采用多目标细菌觅食算法来解决最大化电流效率、最小化能量损耗和全氟化碳生成量的电解铝生产优化问题.作者首先建立了一个面向任务的优化框架，并采用并行细胞熵方法来评估非支配解集的进化状态.该多目标优化方法采用基于非支配存档进化法和自适应觅食方法来平衡优化过程中非支配前沿的分布性和收敛性[49].Kaur提出了一种精英多目标细菌优化算法，该算法采用精英保持策略来求解多标准网格调度问题.实验测试表明，算法优于多目标PSO算法和NSGA-Ⅱ等经典多目标优化算法[50].

总的来说，基于菌群的多目标优化方法在多目标的处理上大多都借鉴了PESA-Ⅱ和NSGA-Ⅱ等经典第二代多目标优化算法，例如精英外部存档、用于拥挤距离的适应度分配等，并在占优机制、进化策略等方面进行了改进补强.

3 菌群优化方法应用研究

除数值优化外，基于菌群的优化方法还被应用于许多工程优化问题中.排名第一的关键词“power”即为其在电力系统中的应用，“application”的词频也排名第四.其他关键词“dynamic”“image”“PID”等高频词也展示了它在动态优化、图像处理、PID控制优化等工程领域中的应用.

除“power”外，关键词“dynamic”“economic”“PID”很大一部分指向的应用领域也为电力系统的动态经济调度(dynamic economic dispatch, DED)和PID稳定性控制等优化问题.电力系统优化是智能算法应用的一个热门方向[51]，前文提到的文献[44-45]也均为电力系统中的应用.

此外，Azizipanah综合考虑电力系统的最优动态优化问题中存储约束、禁止区域、阀点效应等约束，建立了一个非线性、非凸、不平滑、多模态、变量相关、不可微的模型，采用细菌觅食算法-简化群优化混合方法来对该问题进行求解[52].Krishan等提出一种混合的细菌觅食-差分算法，用于电力系统稳定器的设计优化.算法在较宽范围的系统条件和操作下进行了测试，以确保其鲁棒性.特征分析及不同干扰下的时域响应证明了它的有效性[53].Tripathy等将一种改进的BFO算法用于存在多电力系统稳定器和多可控串了联补充电容器的多机电力系统Hopf分叉失稳的参数控制优化[54].Nasiruddin等将细菌觅食算法用于两个地区整合的多源发电站的自动发电机组控制[55].

除电力系统外，还有一些学者将菌群优化算法用于动态环境下机器人路径规划[56-57]、机器人沿墙导航控制[58]、车辆路径规划[59]、制造单元动态调度问题[60]、动态投资组合优化[61-62]、信息动态路由优化[63]等动态优化问题.

在图像处理领域，BFO算法在图像分类、边缘处理、图像配准、图像压缩等技术问题上也有广泛的应用.

文献[64]在径向基函数神经网络中整合了BFO算法，用于图像分类优化，在对参数进行系列调试后，该算法能有效且稳健地解决图像分类问题.Tang等利用改进的BFO算法解决图像处理中多级阈值处理问题.在该算法中，趋化环节借鉴了PSO的算子来增强寻优能力，在繁殖环节中采用了精英保存策略.通过最大化Tsallis阈值函数得到优化解[65].Pan等人针对传统边缘处理算法依赖初值且可能产生不连续边缘的问题，提出了一种基于BFO的边缘检测算法用于细胞图像的处理[66].Verma等采用BFO算法和最小核值相似区法构建一种模糊系统用于图像边缘检测.其中，用BFO算法来优化模糊隶属函数和增强模糊算子的参数[67].Bermejo等将细菌觅食算法用于基于灰度的医学图像配准(image registration, IR)问题[68]，并对细菌觅食算法在图像配准的应用进行了深入研究，通过大量对比发现，细菌觅食算法在该问题上优于其他对比算法[69].Sanyal等将一种变种群的细菌觅食算法用于基于模糊矢量量化的图像压缩问题.该算法能够有效减少训练和重构之间的平均失真问题,采用变化的种群比原始BFO的固定种群更为有效[70].

在PID控制方面，如前文所述，BFO在电力系统的稳定性控制、负载频率控制、自动电压调节器稳压控制等问题中有很多应用.除此之外，菌群优化方法也被应用到很多其他控制问题中.

Abdelkarim提出一种混合的细菌觅食-粒子群优化算法，并将其用于耦合精馏过程中的解耦和控制参数优化.时域结果分析表明，相对于传统PID控制方法有显著的改进[71].Arya等采用细菌觅食算法对多区域互连传统/重构电力系统模糊控制器的增益进行了优化[72].Li为了改善可变风量空调系统的变风量性能，提出了一种基于细菌觅食算法的PID控制策略.首先建立一个非线性的PID控制模型并分析其参数，然后用BFO算法对参数进行调整优化[73].陈东宁等结合粒子群和细菌觅食算法，提出一种混合算法.采用粒子群的位置更新公式来指导菌群的趋化方向，并将其用于材料试验机电液位置伺服系统的PID控制器参数寻优，取得了较好的效果[74].

此外，随着近几年机器学习和大数据技术的兴起，菌群优化在这些方面的应用也大幅增加.以“bacterial foraging optimization”和“machine learning”作主题组合查询一共有文献30篇，全部为2007年之后的，其中2014—2017年20篇，占比66.6%.

Kora等采用混合的BFO和PSO算法，进行心电图信号的特征选择，将特征值作为Levenberg-Marquard神经网络分类器的输入，从而诊察束支传导阻滞，以进行心脏疾病的诊断[75].Wang等人提出了一种离散的细菌觅食算法用于微阵列基因表达癌症数据分类中的特征选择.针对基因表达癌症数据因高维难以分类的问题，通过离散细菌优化算法选择合适的特征以进行数据降维[76].Panda等提出一种自适应交叉细菌觅食算法，采用自适应的趋化来提高寻优效率，并引入交叉因子来加强邻域搜索.该算法被用于人脸识别，以进行数据降维，从而获得人脸识别分析数据中的最优主成分[77].Wu等提出一种基于细菌觅食算法的混合高斯支持向量分类机，用于肌电图信号的疲劳分类.在这一过程中，用细菌觅食算法来进行高斯支持向量机的参数优化[78].

综上，随着细菌优化算法的不断改进，其在工程问题上的应用也越来越多.

4 菌群优化方法发展方向展望

从上述菌群优化的算法改进和应用来看，在过去十几年中，基于菌群优化的研究有了长足的进步.参数改善、多算法混合、算子改善等将依然是算法改进研究的重要方向.然而，现有研究也还有一些内容有所欠缺，值得我们继续深入研究.

细菌及菌群行为特征提取的多样化.从菌群优化研究来看，目前研究主要还是以BFO算法作为基础展开，其核心模拟的是大肠杆菌的趋化行为.除该趋化性和莫宏伟教授MBOA算法的趋磁性外，少有对细菌其他特性的模仿.而自然界中的细菌种类繁多，行为特性也各不相同，如何继续提取一些其他细菌或菌群的典型特征，如细菌的诱导剂分泌、pH值改造，菌群的拮抗、合作现象等以用于优化，是细菌优化方法改进的一个突破方向.

多种群多层次建模.现有的菌群优化方法大多是单一种群，采用相对统一的进化规则和信息交互规则.从自组织的角度看，不利于智能的涌现.利用上述菌群间协作、竞争、拮抗等生物现象建立多层次的拓扑结构及信息交互，并在不同菌群内部采用不同的进化规则，从而保持一定的多样性、非线性和种群进化动力，可能能够更好地促进智能的涌现，以达到优化的目的.目前，一些学者已经展开了多种群粒子群算法的研究[79-80].而多菌群的优化研究较少，尚在起步阶段，值得进一步深入研究.

基于相对位置的更新.在2.1节中已经对比了基于相对位置更新和绝对位置更新的区别，也指明了基于绝对位置更新存在的不足.原始BFO算法采用基于绝对位置更新的趋化操作，虽然很形象地模拟了细菌趋化觅食的生物现象，但不利于算法的收敛.在2.1节的算法改进中，有部分文献借鉴了PSO、DE等算法的算子用个体的相对位置来确定趋化方向，并在趋化步长上采用了一些自适应的方法，但均为通过对趋化步长的控制来平衡全局开发和局部搜索，其本质仍是绝对位置更新.合理改进趋化操作，使之直接采用基于相对位置的更新方式，可能会使菌群优化方法的寻优能力得到新的飞跃.

应用范围的进一步扩展.从应用领域的统计情况来看，目前菌群优化方法在电力系统的优化控制上应用占比非常高，在一些新兴领域也有一些运用，但还不够发散.随着算法的优化能力进一步加强，可以预见的是，菌群优化算法的应用范围也会越来越广.

5 结论

对菌群优化方法进行了介绍，结合近几年的相关文献，从参数与结构改进、多算法混合改进、算子改进和多目标优化改造4个方面对算法改进进行了系统论述，并介绍了其在电力系统、动态优化、图像处理、PID控制和机器学习等工程领域的应用情况.结合现有研究的趋势和存在的不足，对未来发展方向提出了展望.