织物K-M光学参数随染料浓度变化的研究

杨志晖

(中原工学院 纺织服装产业研究院，河南 郑州 450007)

在许多工业比较发达的地区，和着色相关的产业广泛应用计算机进行配色、生产与销售，例如纺织印染、染料、颜料、涂料、塑料着色加工还有油墨等各种行业，并且具有较高的普及率。目前应用计算机进行配色的方式，大都以Kubelka-Munk理论作为基础，首先找出标样按配方混合后颜料光谱反射率的关系，通过色度计算，从混合颜料和颜色间的内在规律确定较为准确的颜料配方。

Kubelka-Munk理论最早出现在1931年，然而到了1958年才逐渐被完全用在纺织印染与印刷行业，从上世纪70年代开始就应用了这种理论。美国和日本等许多国家研发的计算机配色体系大致就是应用此种理论。可是K-M理论在具体运用过程中，它的理论计算和实际过程间依然存在一定的差异。因此，有必要进行计算机配色的相关课题研究。

1 计算机配色的相关理论

Kubelka P.(库贝尔克)和Munk F.(芒克)于1931年发表了能同时进行光吸收和光散射的物理和数学模型[1]，后来Kubelka又分析研究了这种模型，渐渐产生了Kubelka-Munk理论。Kubelka-Munk理论在颜色科学领域起着至关重要的作用。在透明质中，吸收质浓度和吸光系数之间成正比例关系，也就是与Lambert-Beer定律相似；1940年，当Duncan运用Kubelka-Munk理论去对油漆配色进行分析时，假定颜料里各种色料具有的吸收与散射系数和透明介质之间存在相像的特点[2]。1942年，Saunderson也采用了类似假设[3]。之后，这种假定被广泛使用，被称为“色料加和混合定律”[4]。伴随人类对于颜色方面的研究不断深入，逐渐把Kubelka-Munk理论与“色料加和混合定律”共同运用起来，渐渐产生了Kubelka-Munk双常数理论。之前的学者们又假定着色剂具有的散射和某种支撑基质(如纺织品、纸张等)对比是能够不计的，基质内加入着色剂以后的散射系数几乎保持恒定，推导出了Kubelka-Munk这种单常数理论。Kubelka-Munk双常数与单常数两种理论目前在颜色领域中被当作颜色预测根本理论应用。此外，其还是计算机配色过程中的基本理论。在具体使用时，Kubelka-Munk双常数与单常数理论所达到的效果不是很理想。

大多数学者能够找到并认真分析运用Kubelka-Munk双常数与单常数这两种理论过程中出现的问题，然后进行修正。徐海松[5]教授在1999年给出了相对简单的校正方法，忽略表面上的反射以及织物表面内反射，让计算过程变得更加简便。2004年，Yang Li等人重新对Kubelka-Munk理论做出了校正，让它在均匀的介质还有非均匀的介质内的光传播具有一定的框架，同时处理了纸上运用的许多问题[6, 7]，然而这种方案受到了质疑[8-10]。2007年，东华大学的教授何国兴[11]曾运用数学的方式研究出了一种新的双常数理论，和之前的染色数据进行对比，新理论下获得的配方，其染色结果与标准值更加接近。而在2013年，国防科技大学的教授赵龙曾帮助洪铁[12]等几个研究生利用配色半透明涂料时对采集点展开3次样条插值，对低浓度点具有的反射率进行修正，修正之后的结果与Kubelka-Munk理论的线性关系更加接近。

2 实验

(1)实验样布：白色涤纶织物

(2)实验仪器：FA2004B电子天平，织物厚度仪，上海千立自动化染料滴液机，瑞比ECO DYER 高温高压染色机，X-Rite电脑测配色仪

(3)实验试剂：分散染料红、黄、蓝、黑

(4)实验助剂：冰乙酸(调节pH=5-6)

(5)织物规格：平方米克重为52.403g/m2，

厚度为0.0946mm，

经密为419根/10cm，

纬密为320根/10cm。

(6)浴比：1:50

(7)单色owf(%):0%、0.01%、0.03%、0.06%、0.1%、0.2%、0.3%、0.5%、0.7%、1%、1.5%、2%、2.5%、3%、3.5%、4.5%、6%、8%

拼色owf(%):0.06%、0.3%、0.66%、1.26%、2.1%、3.18%、4.62%、6.48%、8.88%

(8)染色工艺:

图1 染色工艺流程

按照上述方法，制备红、黄、蓝、黑色单色染色样品以及双拼、三拼织物样品。

3 测试与结果分析

3.1 测色

本次实验采用的X-Rite电脑测配色仪测试基本参数见表1所示。

表1 测色参数

在测量无穷层厚度时将将染色样品折叠层数为16层；对单层反射率进行测量时应该借助时全吸收黑筒测试样品的R，也就是把黑筒放于单层织物的后边然后开始测试。因为此时所要进行测试的样品其背后正好出现一个黑井，所以真正得到的测试结果就是半球反射比R，倘若忽略表面反射，此R即相当于K-M理论中的R0。

3.2 数据计算

根据已有的织物光学模型，利用公式(1)～公式(7)以及K-M理论，可以计算织物的K-M吸收与散射系数K和S，还有K/S的比值。

(1)

(2)

(3)

(4)

K=S(a-1)

(5)

式中：K和S—着色物的K-M吸收系数(cm-1)和散射系数(cm-1)；

K/S—染色织物的吸收系数与散射系数之比，简称K/S值；

R∞—无穷厚时的反射率；

X—织物厚度mm；

R0—背衬完全吸收衬底的反射比。

公式(4)中需要用到反双曲余切，双曲余切和反双曲余切的计算公式如下：

(6)

(7)

3.3 K-M光学参数与染料浓度关系

根据计算出的织物的K-M光吸收与散射系数K和S，以及K/S，并利用统计软件Origin分析织物K-M光学参数随染料浓度的变化规律，制作图表加以说明。

在Origin软件中依次对红、黄、蓝、黑四色单色涤纶染色织物，以及红色与蓝色双拼涤纶染色织物，黄色与红色双拼涤纶染色织物，蓝色与黄色双拼涤纶染色织物，红、蓝、黄三拼涤纶染色织物的吸收峰位置的K/S、K与S依次与浓度C进行坐标图绘制，结果见图2。

(a)单色染色织物的K/S与浓度C的关系曲线

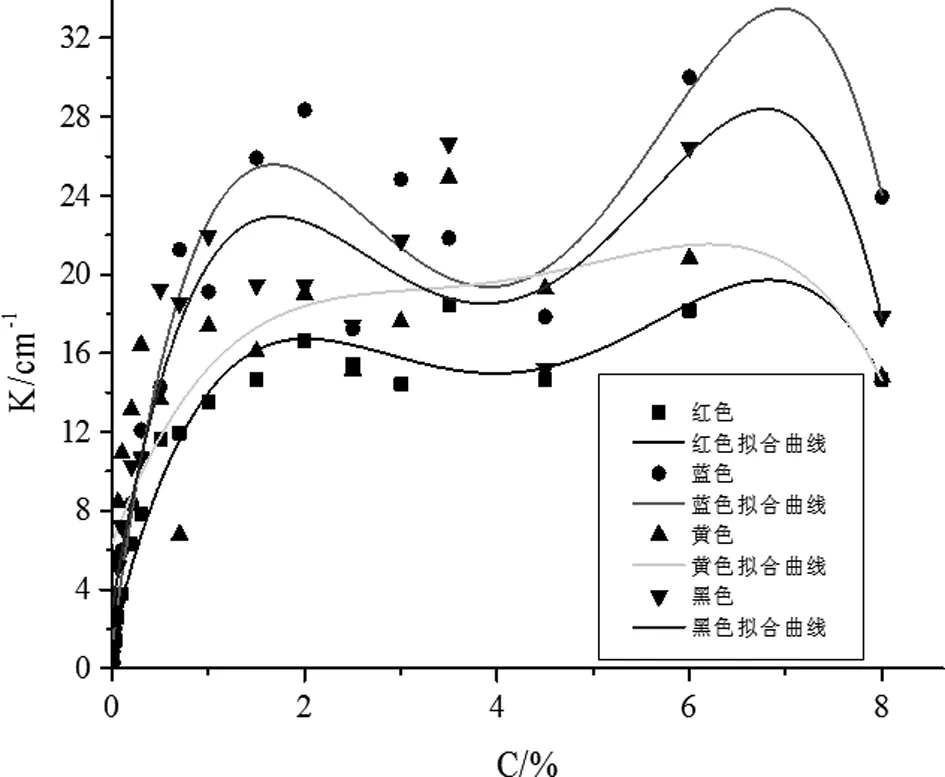
(b)单色染色织物的K与浓度C的关系曲线

(c)单色染色织物的S与浓度C的关系曲线

(d)拼色染色织物的K/S与浓度C的关系

(e)双拼染色织物的K与浓度C的关系

(f)拼色染色织物的S与浓度C的关系

根据图2的数据图表可以看出，红、黄、蓝、黑四色单色涤纶染色织物，以及红色与蓝色双拼涤纶染色织物，黄色与红色双拼涤纶染色织物，蓝色与黄色双拼涤纶染色织物，红、蓝、黄三拼涤纶染色织物K与浓度C的关系曲线以及S对浓度C的关系曲线在吸收峰处K以及S高度负相关。并且单色与拼色染色涤纶织物的K-M吸收与散射系数K和S，还有K/S对浓度C的变化态势是一样的。

应用分散染料时常采取的浓度范畴，制作单色料与多色料的涤纶织物，通过研究涤纶织物实验过程中获得的数据，通过分析图不难看出只有当浓度较低的时候，织物的K/S和浓度C间具有一种线性关系，由于浓度逐渐升高，K/S的值渐渐向浓度C轴方向偏转；织物具有的K会伴随浓度C的升高而升高，但是升高到相应的程度后，升高的态势就显著降低，同时趋于一个稳定值；织物具有的S则正好相反，伴随浓度C的降低而减少，但是降低到相应的程度后，降低的态势就显著减缓，同时趋于一个稳定值；色料加和混合定律和具体情况不符的，光吸收和散射系数K和S不存在加和性；具体运用过程中，应该对K-M理论以及色料加和混合定律进行相应的修正。因为K-M理论以及色料加和混合定律本身具有一定的问题，使得K-M的双常数与单常数这一理论在具体运用中能够配色一次成功的概率低。

实验表明，“色料加和混合定律”这一理论和实践间是有一定差别的，因此在运用过程中需要进行修正处理，而由于有差异所以使得计算机在配色过程中的成功率比期待值低。

4 结论

根据光学模型公式能够求出织物K-M的K、S和K/S的值，并分析它们与染色浓度之间的关系。实验结果表明无论是单色染色织物还是双拼色以及三拼染色织物，织物的K-M吸收与散射系数K和S，还有K/S对浓度C所产生的变化是一样的。现总结如下：

(1)K/S会跟随染料浓度的升高而升高，当浓度比较低的时候呈现出相应的线性关系，当超出相应的浓度之后不再成线性关系；

(2)色料的K和浓度C之间不成正比例关系，当浓度比较低的时候呈现出相应的线性关系，当超出相应的浓度之后不再成线性关系；

(3)同样，散射系数S也不具备与浓度C的线性关系，在浓度较低时成线性关系，超过一定浓度后不成线性关系；

(4)色料所具有的散射系数会其吸收波段伴随浓度升高而降低，这与色料混合定律色料所具有的散射系数色料的浓度升高而升高不同；

(5)吸收与散射之间会互相受到影响，K与S在吸收波段呈现出高度负相关。

由此可以得出：这种“色料混合加和定律”目前还有很多不足之处。通过本文可以对织物K-M光学参数K、S，还有K/S和C之间的关系有个系统的了解，可以更好地结合K-M单常数和双常数这两种理论在实际情况中的运用。