广义拟向量变分不等式与拟近似解
马 圆 圆
(重庆师范大学 数学科学学院,重庆 401331)
0 引 言
向量变分不等式(简称VVI)的概念首次在文献[1]中提出,一些学者已经研究了向量优化问题(简称VOP)与凸性或广义凸性条件下的向量变分不等式之间的关系[2],这些研究说明多目标优化问题的最优性条件可以由VVIs来刻画.近年来,凸性的概念不断被推广,如文献[3]提出了近似凸性的概念,文献[4]提出了广义E-凸函数的概念和性质.
在VOP问题中,有效解是一个被广泛应用的概念.文献[5]利用近似凸性的假设和拟有效性的概念,研究了VOP问题中的近似凸性;Mishra和Upadhyay在文献[6]中研究了VVIs和非光滑VOP问题之间的关系;Mishra和Laha在文献[7]中建立了近似VVI的解作为VOP问题的近似有效解的充分和必要最优性条件;Yang和Zheng在文献[8]中得到了VVI的解的充分和必要最优性条件;Lee等人在文献[9]中建立了不同类型的VVI与非光滑多目标优化问题之间的关系;文献[10]定义了KT-严格近似(KT-近似)伪凸仿射函数的概念,研究了广义Stampacchia VVI与多目标优化问题之间的关系.
受文献[10]的启发,本文通过利用两类新定义的广义凸函数,在合适的约束品性条件下,Kuhn-Tucker向量临界点、多目标优化的解与广义Stampacchia VVI在弱和强形式下解之间的关系将会被证明.
1 预备知识
在本文中,需要以下偏序关系:对任意的x,y∈Rl,有
x=y⟺xi=yi,∀i=1,2,…,l
x≤y⟺xi≤yi,∀i=1,2,…,l
x x≤y⟺x≦y,且x≠y 考虑如下的多目标优化问题: (MP) minf(x)=(f1(x),…,fm(x)) s.t.g(x)=(g1(x),…,gm(x))≦0 h(x)=(h1(x),…,hm(x))=0,x∈Q 这里,fi,i∈I={1,…,m};gj,j∈J={1,…,n};hk,k∈K={1,…,p}是Rl中的实值局部Lips-chitz函数,Q∈Rl是任意集;有效指标集记为J(x0).MP问题的可行集定义为 S={x∈Rl:g(x)≦0,h(x)=0,x∈Q} 定义1[11]φ:Rl→R是局部Lipschitz函数,φ在x处沿方向v的Clarke广义方向导数记为φ°(x;v),定义为 定义2[11]φ:Rl→R是局部Lipschitz函数,φ在x处的Clarke广义次微分记为∂Cφ(x),定义为 ∂Cφ(x)={ξ∈Rl:〈ξ,ν〉≤φ°(x;ν),∀ν∈Rl}. 下列推论是文献[10]的推论2.1结果的直接推广. (1) 下列系统无解: ≦0 ≦0 文献[5]中介绍了MP问题的局部(弱)拟有效解的概念,这里给出局部(弱)近似拟有效解的概念. (1) (2) 可行点x0是MP的局部弱近似拟有效解(近似弱拟有效解)当且仅当存在 和x0的邻域U,使得x∈U∩S(或x∈S),下列不等式(2)不成立: (2) 定义4[10]可行点x0是MP的Kuhn-Tucker向量临界点(简称KTVCP)当且仅当存在 且 使得 N(Q,x0),μjgj(x0)=0,∀j∈J 下面给出两类新的广义凸函数定义. 定义5 令x0∈S,MP问题在S上x0处是近似(严格近似)拟伪凸仿射函数,若对于任意 存在δ>0,使得对每一个 进而有下列不等式(3)成立: h°(x0;x-x0)≦0,(-h)°(x0;x-x0)≦0 x-x0∈TC(Q,x0) (3) 文献[10]中介绍了广义(弱)Stampacchia向量变分不等式的概念,下列定义6和定义7给出广义(弱)Stampacchia拟向量变分不等式的概念. (4) (5) 证明与定理1证明类似. (6) 证明与定理3证明类似. 证明与定理5证明类似.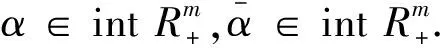



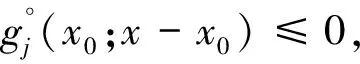

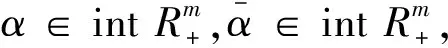
2 主要结果及证明
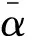
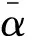
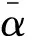
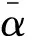
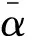
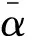

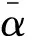
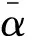
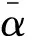
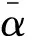
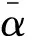
3 结 论