组合隔震系统基于负刚度装置的隔震效果研究
杨巧荣 任天娇 何文福 于维欣
(上海大学土木工程系,上海 200072)
0 引 言
基础隔震是目前应用最为广泛的结构振动控制技术。隔震技术不仅在民用建筑和桥梁工程中得到广泛的应用,而且在许多重要的基础设施及核电领域中得到应用[1-2]。对于传统的被动隔震技术要实现低频隔震,必须减小结构的自振频率,即减小结构的刚度。虽然在一定程度上能降低结构整体的加速度响应,但隔震层变形过大容易导致出入隔震层的管线在连接处附近遭到断裂破坏,同时存在结构碰撞、支座竖向承载力下降等问题。因此,采用负刚度的控制思想,将负刚度装置与橡胶支座组合使用,抵消橡胶支座的正刚度,使隔震层具有更低刚度,同时提高结构的阻尼比,获得更优的隔震控制效果。
从目前的研究状况看,负刚度理论首先被应用于机械设备和精密仪器的振动控制领域,大多数是进行隔振方面的应用研究。在国外方面,Iemura[3]首先提出了结构负刚度振动控制,研制了负刚度阻尼构件,与普通橡胶支座组合形成新型隔震系统,并进行振动台试验研究,验证了该隔震系统可以大幅减小结构的位移和加速度响应;Iemura[4]提出了一种拟负刚度控制算法,并通过数值分析就斜拉桥的二阶段benchmark问题比较了被动控制、半主动控制和主动控制的效果,结果表明该半主动控制的效果优于被动控制,接近主动控制;Igrashi[5]等对负刚度控制系统的性能进行了进一步的评估分析,说明了负刚度控制系统在土木结构的振动控制方面的确有效果。Attary[6]通过大量的数值分析隔震桥梁模型,研究表明当甲板位移控制在合理的范围内,负刚度装置能有效减小基底剪力。在国内方面,张建卓等[7]提出了通过正负刚度弹簧并联实现超低频隔振的新方法,研究表明由于并联了负刚度弹簧,隔振系统固有频率从6 Hz降低到0.75 Hz,隔振能力明显提高。李慧等[8]对斜拉索减震的主动和半主动控制的负刚度特性及影响进行了研究,提出了负刚度的量化标准的三项指标;吴斌等[9]对拟负刚度与黏滞阻尼混合减震的效果进行了理论分析,并釆用实时混合试验方法对多自由度结构的拟负刚度与黏滞阻尼混合控制效果进行了研究;纪晗等[10]提出了在普通隔震层附加负刚度阻尼装置(NSD)的新型隔震系统,并讨论了NSD对隔震系统性能的影响,研究表明新型隔震系统可以实现长周期结构隔震;龚微[11]基于国际通用Benchmark隔震模型,提出了一种基于磁流变阻尼器的负刚度智能隔震控制策略及一组有效控制参数,研究了不同断层距的近场地震下不同控制方式隔震结构地震反应。
基于目前的研究进展,本文提出了一种附带阻尼水平向负刚度装置,首先通过预压碟形弹簧和拱球面提供与运动方向一致的负刚度水平恢复力;然后建立附带阻尼的水平向负刚度装置的力学模型,并对其性能影响参数进行分析,最后通过MATLAB软件建立多自由度模型,对负刚度组合隔震模型在强震下所产生的动力响应进行分析,并与常规隔震系统的隔震效果进行对比,验证了负刚度组合隔震系统的有效性。
1 附带阻尼水平向负刚度装置及其力学模型
1.1 附带阻尼水平向负刚度装置
运动过程中,碟形弹簧与阻尼器协同工作,同时产生竖向恢复力和阻尼力作用于拱球面。拱球面对球铰的支持力的水平分力,提供负刚度水平恢复力,恢复力背离平衡位置,如图2所示。通过设置限位杆,防止结构摇摆,保证预压碟形弹簧只在垂直方向发生变形。

图1 负刚度装置示意图Fig.1 Schematic diagram of negative stiffness device

图2 负刚度装置运动示意图Fig.2 Schematic diagram of motion of negative stiffness device
1.2 力学模型
碟形弹簧刚度为k,拱球面曲率半径R,球铰半径r,水平位移u,碟形弹簧竖向恢复变形增量v,θ为滚轮中心偏离平衡位置的相对角度。
θ与水平位移u和竖向变形增量v的关系为
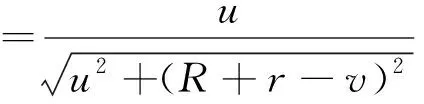
(1)

(2)
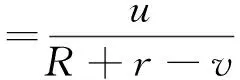
(3)
(4)
由式(3)和式(4)即可推出水平变形u与竖向变形增量v之间的关系:
v2-2(R+r)v+u2=0
(5)
令B=R+r,可得:
(6)
碟形弹簧的竖向恢复力FV为
FV=k(γ0-v)
(7)
式中:γ0表示初始时刻碟形弹簧的压缩长度。
对拱球面部分图3(a)的受力分析可知:

(8)
式中:FN表示拱球面对球铰的支持力;FV表示碟形弹簧的竖向恢复力。
拱球面对球铰的支持力的水平分力FNX用于提供负刚度水平恢复力。
对球铰部分图3(b)的受力分析可知:
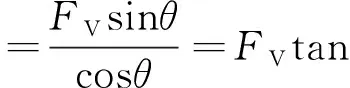
(9)
将式(3)、式(6)、式(7)代入式(9)即有:
(10)
式中:FNX表示负刚度水平恢复力;B表示球铰与拱球面的球径之和。
将式(10)对水平位移u求一阶导,即可求得
负刚度KN与水平位移u的关系式:
(11)
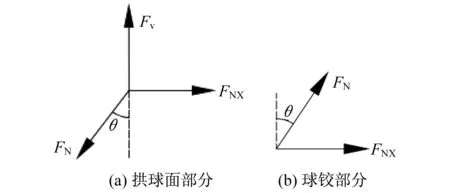
图3 受力分析图Fig.3 Stress state

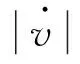

(12)
阻尼力的水平分力FDH作为负刚度装置的阻尼力
FDH=FDtanθ=
(13)
1.3 附带阻尼负刚度组合隔震系统
附带阻尼负刚度组合隔震系统由附带阻尼负刚度隔震装置和铅芯橡胶支座共同组成。铅芯橡胶支座屈服后刚度为K2,假定初始刚度K1为屈服后刚度K2的13倍;由此可得组合隔震系统的初始刚度为K1+KN,屈服后刚度为K2+KN。该隔震系统力学模型如图4所示。
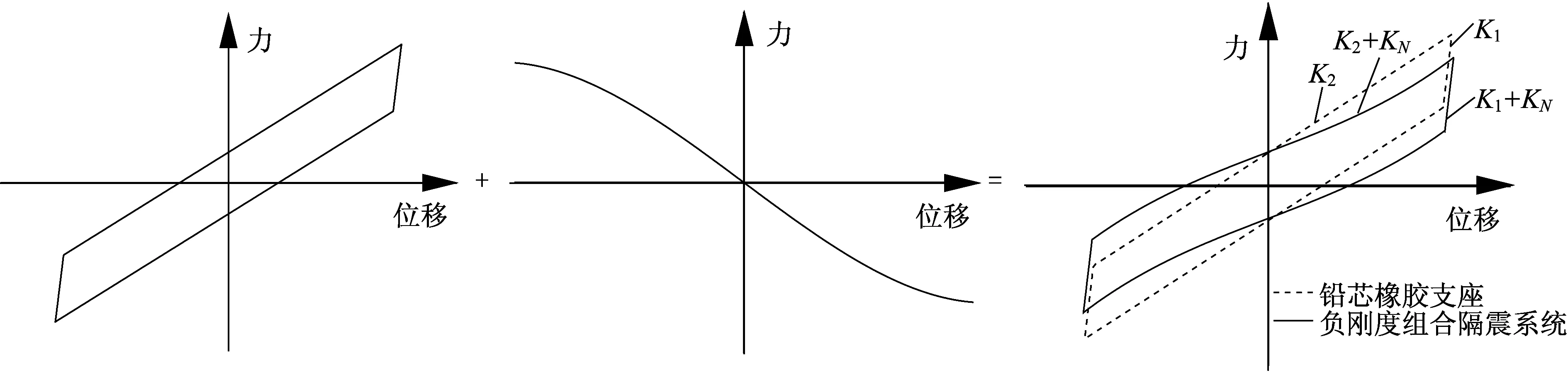
图4 负刚度组合隔震系统力学模型Fig.4 Mechanical model of combined isolation system with negative stiffness
2 力学参数分析
2.1 负刚度与碟形弹簧刚度k的关系
碟形弹簧竖向刚度k对该支座水平负刚度的影响差异较大,根据公式(11)可以得出不同碟形弹簧竖向刚度k与负刚度KN的关系曲线,如图5所示。
从图5中可以看出,负刚度随着碟形弹簧刚度的增加而增加,但对负刚度的行程范围没有影响。
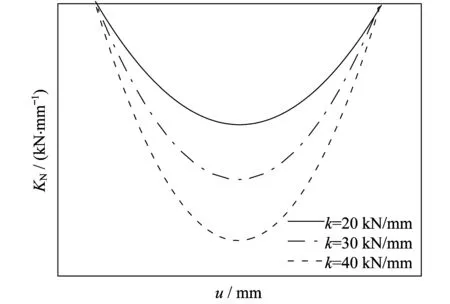
图5 负刚度与碟形弹簧刚度的关系Fig.5 Correlation between negative stiffness and stiffness of disk spring
2.2 负刚度与球径之和B的关系
通过控制球径之和来改变滚轮滑动所产生的转角,从而决定提供负刚度的水平力范围。由公式(11)可知,球径之和改变对负刚度KN的大小和负刚度行程范围都有一定的影响。负刚度与球径之和的关系曲线如图6所示。

图6 负刚度与球径之和的关系Fig.6 Correlation between negative stiffness and sum of sphere diameter
由图6可知,随着球径之和B的增大,负刚度KN随之减小,并且负刚度的行程范围随之增大。因此,合理设置球径之和B的参数,对该装置性能的影响至关重要。
2.3 负刚度随预压变形γ0的变化
通过预压变形对该负刚度装置产生预压力,提供水平向负刚度力。由公式(11)可知,预压变形γ0与负刚度KN的关系,如图7所示。
由图7可知,随着预压变形γ0的增大,该装置的负刚度KN越大,负刚度的行程范围也随之增大。

图7 负刚度与预压变形的关系Fig.7 Correlation between negative stiffness and pre-compression deformation
3 负刚度组合隔震系统时程分析
3.1 计算模型
本文通过MATLAB软件建立负刚度组合隔震系统多质点模型,并对负刚度组合隔震模型在强震下所产生的动力响应进行分析。隔震模型周期为2.6 s,单个支座的基本面压为7.5 MPa。模型采用本文提出的负刚度力学模型,并以纽马克-β非线性加速度法进行时程计算。简化模型如图8所示。图中,Kiso表示隔震层刚度,KN表示负刚度,C表示阻尼系数。
3.2 时程分析
时程分析采用三条地震波,分别为El Centro(简称EL波)、Ha波、Tang Shan波。地震波峰值从0.3g开始逐次递增至0.6g,模拟负刚度隔震模型和隔震模型在不同等级地震下的响应。

图8 多质点简化模型Fig.8 Multi-particle model
表1为隔震模型(LRB)和负刚度隔震模型(NSD)在EL波、Ha波、Tang Shan波三条地震波作用下,隔震层位移峰值的均值对比。地震波峰值较小时,负刚度隔震模型较隔震模型位移减小率较小,随着地震波峰值的增大,两种模型的位移减小率也随之增大,且最大偏差率为19.51%。
表2为三条地震波作用下,楼层加速度响应峰值的均值对比。从计算结果可以看出,在峰值为(0.3~0.6g的地震波作用下,负刚度隔震模型相比隔震模型的加速度均有所减小,且最大偏差率为29.64%。负刚度组合隔震模型不仅能控制隔震层的变形,同时能降低隔震层及上部结构的加速度响应。
表1三条地震波作用下隔震层位移峰值的均值对比
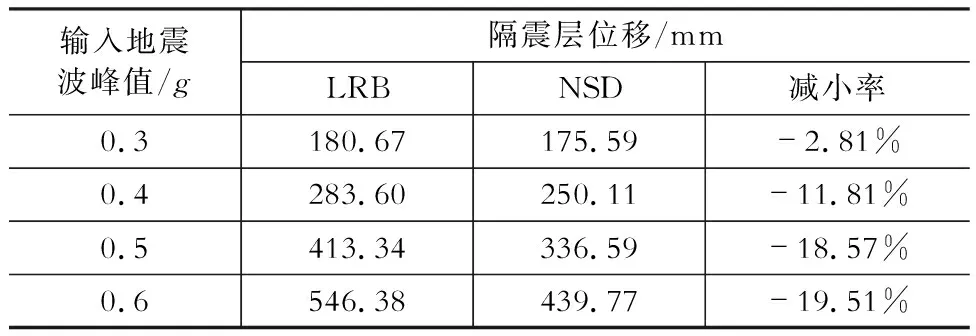
Table 1Comparison of mean value of displacement peak of seismic isolation layer under three seismic waves
表2三条地震波作用下楼层加速度响应均值对比
图9为质点系模型在峰值为0.6g三种地震波作用下的隔震层加速度反应谱对比。由此可知,负刚度组合隔震模型加速度反应谱峰值均小于隔震模型的峰值。在反应谱低频段,偏差较大;在高频段,加速度反应谱谱值差异较小。负刚度组合隔震模型的加速度响应较隔震模型的加速度进一步减小。
图10为质点系模型在峰值0.6g三种地震波作用下的隔震层滞回曲线对比。可知,相比隔震模型,负刚度组合隔震模型的位移减小10.42%至28.05%之间。隔震层经历过一次大变形后,吸收了更多地震能量,因而在反向加载时隔震层变形控制效果显著。相比隔震模型,负刚度组合隔震模型使得隔震层滞回曲线更加饱满。
图11为质点系模型在峰值0.6g三种地震波作用下楼层加速度峰值包络图。可知,负刚度组合隔震模型相比隔震模型的加速度峰值均减小。隔震层加速度响应峰值降低区间为12.16%至27.10%;其他楼层加速度峰值降低区间为10.81%至31.67%。负刚度组合隔震模型的整体隔震效果较隔震模型更显著,能更好地控制强震下隔震层及上部结构的加速度响应。
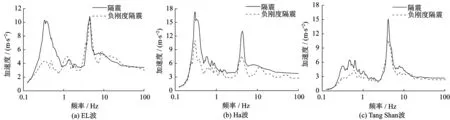
图9 峰值0.6 g不同地震波作用下隔震层加速度反应谱对比Fig.9 Comparison of acceleration response spectrum of seismic isolation layer under different seismic waves at peak of 0.6 g

图10 峰值0.6 g不同地震波作用下隔震层滞回曲线对比Fig.10 Comparison of hysteresis loops of seismic isolation layer under different seismic waves at peak of 0.6 g

图11 峰值0.6 g不同地震波作用下加速度峰值包络图对比Fig.11 Comparison of acceleration peak envelope diagram under different seismic waves at peak of 0.6 g
4 结 论
本文通过对一种附带阻尼水平向负刚度装置的理论分析,并对其与隔震支座协同工作的组合隔震系统的隔震效果进行研究,可得到如下的结论:
(1) 提出一种附带阻尼水平向负刚度装置。该装置由球铰上、下连接板、球铰、拱球面、预压碟形弹簧、黏滞阻尼器、限位杆和支承底座组成,具有低频隔震、布置灵活的特点。负刚度装置由碟形弹簧竖向恢复力及阻尼力对拱球面的径向提供负刚度水平恢复力,且负刚度在设计范围内随着隔震层变形增大而减小;同时阻尼力进一步控制由于刚度降低而放大的隔震层变形。
(2) 建立多质点模型进行动力时程分析,得出负刚度组合隔震模型相比隔震模型的加速度均有所减小,且隔震层最大减小率达24.77%,上部结构最大减小率达29.64%。负刚度组合隔震系统隔震效果显著。
(3) 负刚度组合隔震模型的隔震层位移减小率随着地震波峰值的增大而增大,且隔震层最大变形减小率达19.51%。隔震层经历过一次大变形后,吸收了更多地震能量,因而在反向加载时隔震层变形控制效果显著。相比隔震模型,负刚度组合隔震模型使得隔震层滞回曲线更加饱满。

