基于运动传感器的帕金森自动分级研究

杨越，汪丰，孙丰，郑慧芬

1.东南大学 生物医学与科学工程，江苏 南京 210000；2.南京医科大学附属脑科医院 a.神经内科；b.老年神经科，江苏 南京 210029

引言

帕金森病（Parkinson’s Disease，PD）是一种慢性的中枢神经系统退化性疾病，会对患者的运动、语言和其他功能造成损害，多发于中老年人[1]。据调查，中国目前PD患者人数已有200余万人。对于PD精准的治疗和监测关键要求是对疾病阶段和严重程度测量是定量的，可靠的和可重复的[2]。PD研究的最近50年一直以主观评分为主，这些评分是通过人为观察和分析临床疾病特征的表现而获得的。PD的运动功能评价是康复治疗的重要内容，其对评估药物效果，指导制定治疗方案和辅助诊断等具有重要作用。目前临床上主要依靠相关评分量表对各项指标进行打分，比如Hoehn&Yahr量表、Webster量表和Unified Parkinson’s Disease Rating Scale（UPDRS）等。

临床渴望能尽早诊断患者的临床症状、监测疾病进展并迅速找到最佳的治疗方案。患者希望提高生活质量，同时减少体检门诊，患者护理力求尽量减少对门诊的依赖，并转入患者家中。最近，已经开发了基于传感器的“可穿戴”系统，定量、客观和易于使用地用于量化PD症状。这项技术有可能显著改善PD的临床诊断和管理以及临床研究的进行。然而，这些可穿戴式传感器所捕获的大规模数据和高维度的特征需要复杂的信号处理和机器学习算法来将其转化为具有科学意义和临床意义的信息。

本文从传统量表和临床医学出发，设计一系列表现患者运动功能状态的动作，通过加速度计数据提取特征参数，最终通过先进的机器学习分类方法来预测帕金森病患者的Hoehn-Yahr分期。

1 数据与方法

1.1 数据收集

在2015年9月到2018年2月期间共采集67个人为研究对象，年龄从41岁到80岁。实验组的数据采集自本课题的合作医院南京医科大学附属脑科医院，确诊为PD Hoehn & Yahr分期1到4，即轻度至中度双侧疾病。分期标准，见表1。

表1 Hoehn-Yahr分期标准

实验组对象来自的状态包括服用药物前、服用药物后、深部脑刺激治疗后，与之对应的PD运动分级是由临床医生在进行收集数据实验后立刻执行的。健康对照组来自两家医院的工友、陪护人员等。其中，各个分类人数的比例指的是健康个体数量比上1到4级各级个体的数量。健康组:1级:2级:3级:4级人数比例为11:7:24:17:8，男女比例为1:2，年龄分布为（62.8±8.5）岁。

受试者被指导执行一系列标准化的运动任务，用以评估PD患者的临床情况。这些运动任务根据统一帕金森病评定（UPDRS）量表制定，运动任务包括10 m往返行走、双重任务10 m往返行走、反复起坐、双手连续翻腕、静坐交替抬腿、睁眼静止站立、闭眼静止站立、静坐双手平举（姿势性震颤）、静坐双手平放大腿（静止性震颤）[3]。

已有的体域网运动采集系统，见图1，该无线传感器网络包括5个终端采集节点，即三轴的加速度、角速度传感器，分别佩戴在人体的左右脚踝部、左右手腕部和腰部后背中心。采集系统使用MPU6050芯片作为核心传感器，角速度传感器的量程为±2000°/sec，加速度传感器的亮度为±8 g，采样率为50 Hz。数据接收终端通过USB接口与PC机相连，采用串口通讯协议与上位机进行通信，通过近距离无线通信方式，与采集终端进行通信。

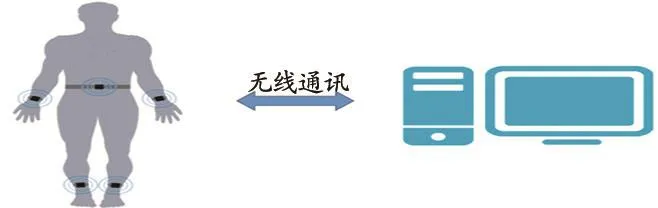
图1 数据采集系统结构示意图

1.2 特征提取

具有代表性的多维度特征提取是算法的基础。本文结合各个任务的运动特征和统计特征来共同描述运动。

1.2.1 数据预处理

由于佩戴位置松动产生的人与仪器的相对运动带来的噪声和采集系统的测量噪声。信号分别通过截止频率为0.25 Hz的2阶巴特沃兹高通滤波器去除佩戴位置带来的基线影响，和截至频率为20 Hz的4阶巴特沃兹低通滤波器去除高频噪声干扰[4]。

对每个独立的运动任务，用5 s矩形窗将30维（有5个传感器，每个传感器有6个轴的信号）信号分割为各不相交的数据段，将每个窗口中的数据段视为一个动作任务的代表。采用5 s的窗口被证明可以提高结果的准确率[5-6]。

1.2.2 运动特征提取

结合UPDRS量表等评测标准以及PD临床专家的意见，从步行分析、平衡能力、姿势转换能力、关节活动能力以及震颤程度5个方面计算运动特征参数。以不同运动功能之间的差异性显著和重复性小作为参数筛选的标准。

步态分析主要从时域和空间域同时分析上肢和下肢的动作，时域参数包括步态周期、双支撑相（双脚与地面同时接触的时间）[7]；空间域参数包括步长、摆臂角速度峰值、摆臂平均角度。分析平衡能力需要对比受试者在有视觉辅助状态下与没有视觉辅助下的控制身体的重心能力，需要分析腰部的传感器，时域参数包括重心动摇距离均方根、重心单位时间轨迹；频域参数包括95%功率频率、质形心频率和重心动摇平滑性。姿势转换能力是通过反复起坐和往返走中的转弯这两个动作来分析的，需要分析腰部的传感器，参数包括完成由坐到站和到由站到坐所需平均时间、反复起坐身体平均弯曲角度、完成转弯所用的平均时间、转弯中身体角速度的峰值[8]。通过连续翻腕和静坐抬腿这两个动作来分别评价上肢和下肢的关节活动能力，需要的参数包括翻腕的平均角度、完成翻腕的平均周期、完成一个抬腿动作的平均周期和每个抬腿周期内的角速度峰值。震颤的评价主要通过静止震颤和动作震颤，分析其3～8 Hz的频谱。以上的时域和空间域参数都需要计算其标准差。

1.2.3 统计特征提取

使用了几个时域和频域上的标准机器学习特征，分别在六轴传感器5 s的窗口截取后的数据上计算。时域统计特征包括标准差的无偏估计、偏度和峰度。频域特征包括主频频率、质心频谱和带宽。其中主频频率表示功率谱最大值的频率。分别使用以下3个公式计算：

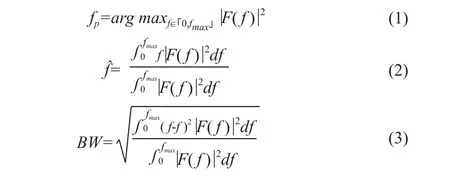
其中F( f )表示信号的傅里叶变换，所求的频率范围是0～50 Hz。

时频域特征是通过小波变换来计算不同的时频段的信号特征[9]。使用Meyer小波[10]对信号进行9层小波分解计算各个时频段下的相对能量。信号的能量通过近似系数的欧几里得范式来计算：

其中a9表示由第九层小波分解的近似系数组成的向量。第k层小波分解的细节系数由下式计算：

使用下面的两个公式来计算每层小波分级对相对能量的贡献：

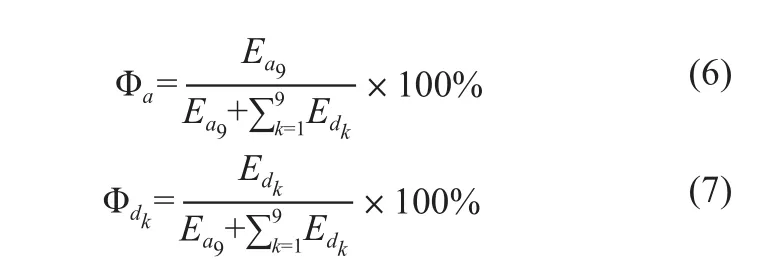
除以上参数之外，也根据波形计算了其他一些参数。通过离散傅立叶变换计算各轴数据的谐波比，公式如下：

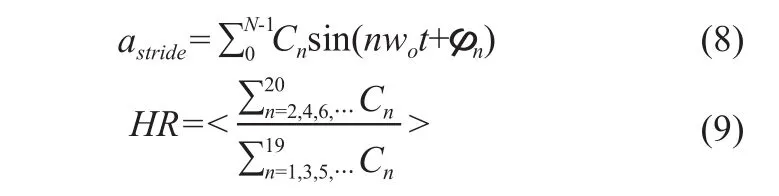
其中Cn是谐波系数；wo是步幅频率；φn是相位。然后将前20个谐波系数相加并用于计算谐波比。

1.3 分级算法

每个训练集实例是各个运动任务中统计参数和运动参数的组合，将特征归一化到[0, 1]区间。得到特征表示后需要选择一种分类器，以根据加速度计和陀螺仪数据的特征来估计PD的H-Y分期。本文对3个目前最先进的分类器：支持向量机（Support Vector Machine，SVM）[11]、K最邻近（K-Nearest Neighbor，KNN）[12]以及随机森林[13]进行比较。由于这些方法在许多分类问题中的成功，并展现出良好的泛化性能。使用python的sklearn工具箱[14]来实现以上分类算法。

分类器的验证标准为“留一法”，如果设原始数据有N个样本，即每个样本单独作为验证集,其余的N-1个样本作为训练集，会得到N个模型。该方法有两个明显的优点：① 每一回合中几乎所有的样本皆用于训练模型，因此最接近原始样本的分布，这样评估所得的结果比较可靠；② 实验过程中没有随机因素会影响实验数据，确保实验过程是可以被复制的。其缺点是稍微增加了验证模型的时间，但是时间消耗在可以接受的范围内。

2 结果

2.1 分类器的比较

2.1.1 支持向量机算法结果分析

由于最终结果有5种不同类别，所以具体实现采用“一对多”的方法解决多类分类问题，以降低计算量，并且通过验证对分类精度没有影响。使用三个不同的内核，即指数（sigmoid）、径向基（rbf）和多项式（poly）内核，并比较结果。使用的多项式核函数的次数为3。随着惩罚系数从1到100增加时，三种内核下分类器的准确率的变化趋势图，见图2。

当我们将错误分类惩罚系数“C”从1增加到100时，由于分类器的复杂性随着“C”值的增加而增加，因此预期每个分类器的准确度会增加。但是观察得到当“C”的值大于5时，指数核与径向基核导出结果准确率降低，最终在保持在65%左右的准确率。对于使用多项式核导出的结果一直随着“C”的增加而增加，直到C的取值在80以上时保持稳定。

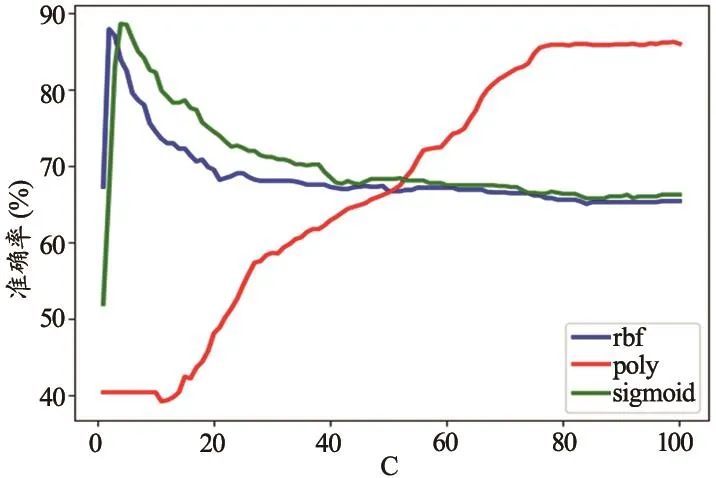
图2 准确率随惩罚系数变化趋势图

2.1.2 K最邻近算法结果分析

KNN的工作原理为：对于测试样本，通过某种计算距离的方式找到训练集中与其最靠近的k个训练样本，根据k个“邻居”的信息来进行预测。样本的权重有“uniform”(为每个邻居分配统一的权重)和“distance”(与距离查询点距离的倒数成比例的权重)两种方法。比较这两种权重选择方法，准确率的变化趋势，见图3。

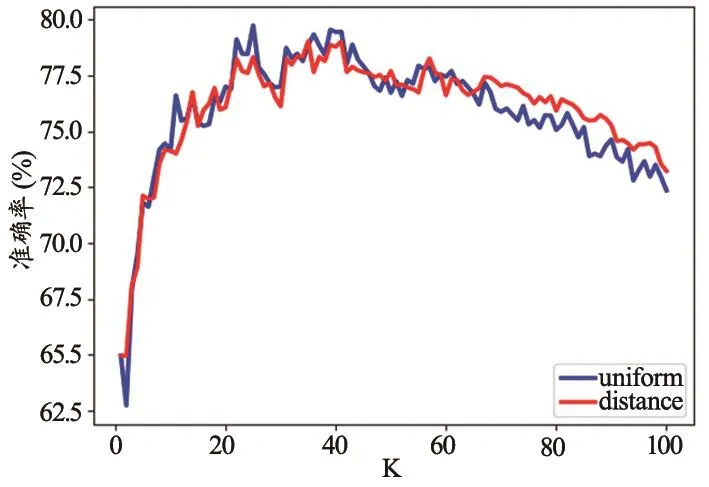
图3 准确率随K值变化趋势图

可以看到随着k的增加两种权重选择方法差异不大，“uniform”方式的准确率稍微高一点。

2.1.3 随机森林算法结果分析

鉴于决策树[15]容易过拟合的缺点，随机森林采用多个决策树的投票机制来改善决策树。有两种测量分割质量的函数，分别是“gini”(基尼杂质)和“entropy”(信息增益)。将随机森林中决策树的数量K从1增加到100，可以看到在决策树的数量小于20时准确率呈现增加趋势，随后保持平稳。两种测量分割质量的函数的差别很小。其趋势图，见图4。

2.1.4 三种算法结果的比较

三种分类器的准确率分别为：支持向量机89.55%，K最邻近79.83%，随机森林86.85%，可以看到支持向量机的分类精度最高。

在分类精度最高的支持向量机中，各类样本的分类情况，见表3，括号中为每类的总人数。

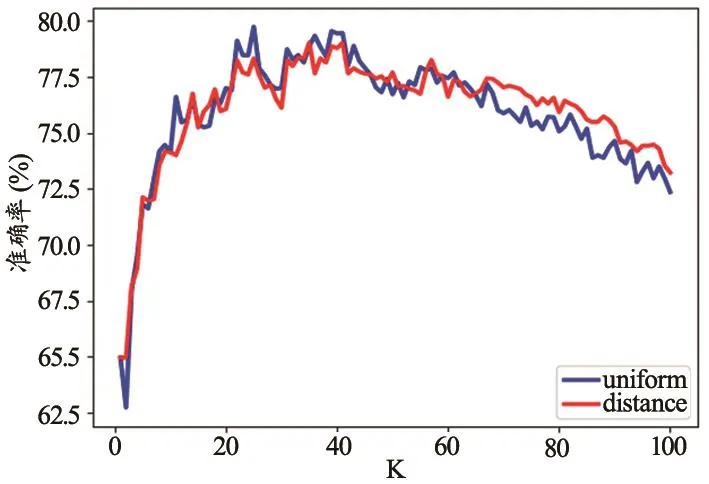
图4 准确率随决策树数量变化趋势图

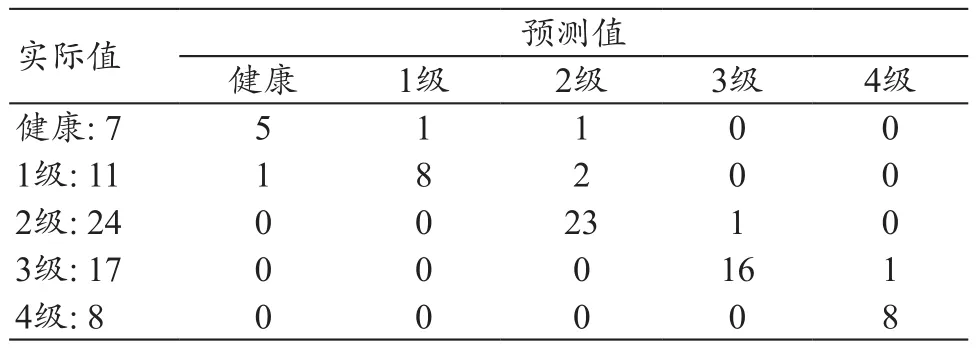
表3 各类分类结果（人）

2.2 参数的选择

本文提取了两种类型的特征参数，分别是运动特征与统计特征。在使用SVM分类器时，单独使用运动特征的准确率为75.52%，统计特征的准确率为78.31%，同时使用两种特征的准确率为89.55%。明显可以看到，同时使用两种特征对提高模型的准确率有很大的帮助。

3 讨论

因为基于运动传感器参数的PD检测系统结合临床需求通过传感器数据与最先进的机器学习算法定量的分析PD患者的运动功能，本研究很好的辅助了PD的临床诊断以及临床研究。在大多数可穿戴设备和机器学习相结合的算法中[2]，特征参数一般都来自时频域上的统计参数，而忽略了一些经典的体现运动特征的参数[7-8]。有效的特征选择和提取是建模成功的关键，而本研究首创合并了运动特征和统计特征来共同建立一个相对全面的特征表达的方法。从实验中可以看到同时加入运动特征和统计特征相较于单独加一种特征分类器的准确率提高了16.42%。同样多个可穿戴传感器节点为模型提供了全面的特征尺度，本研究记录一共5个节点的六轴加速度和角速度数据；相比之下其他研究工作通常只记录1～2个节点的3轴加速度数据[16]。本研究对比了3种最先进的分类器的实验结果，得到的结果数据可以为其他研究者选择分类器时做一个参考。后续研究可以从特征参数降维、特征组合以及多种机器学习模型融合的方法来提高算法准确率。

4 结论

本研究针对PD的自动H-Y分级任务，给出了一种基于运动特征和统计特征的机器学习分类方法。在67例个体中，达到了89.55%的准确率，可以辅助医生的日常诊断。下一步的研究可以使用多模型融合的方法，用多个模型预测到的概率来进行投票，提升单个模型的精度。另一方面深度学习在许多领域取得了非凡的成果[17]，结合深度学习和运动传感器的方法也是一个很好的尝试。

[参考文献]

[1] Poewe W,Seppi K,Tanner CM,et al.Parkinson disease[J].Nat Rev Dis Primers,2017,3:17013.

[2] Kubota KJ,Chen JA,Little MA.Machine learning for largescale wearable sensor data in Parkinson’s disease: Concepts,promises, pitfalls, and futures[J].Movem Dis,2016,31(9):1314-1326.

[3] 乔子晏.基于惯性传感器的PD患者运动功能评价的研究[D].南京:东南大学,2016.

[4] Zwartjes DG,Heida T,van Vugt JP,et al.Ambulatory monitoring of activities and motor symptoms in Parkinson’s disease[J].IEEE Trans Biomed Eng,2010,57(11):2778-2786.

[5] Patel S,Lorincz K,Hughes R,et al.Monitoring motor fluctuations in patients with Parkinson’s disease using wearable sensors[J].IEEE Trans Inf Technol Biomed,2009,13(6):864-873.

[6] Pastorino M,Cancela J,Arredondo MT,et al.Assessment of Bradykinesia in Parkinson’s disease patients through a multi-parametric system[A].International Conference of the IEEE Engineering in Medicine and Biology Society[C].New York:IEEE,2011:1810-1813.

[7] Yang S,Zhang JT,Novak AC,et al.Estimation of spatio-temporal parameters for post-stroke hemiparetic gait using inertial sensors[J].Gait Post,2013,37(3):354-358.

[8] Salarian A,Horak FB,Zampieri C,et al.iTUG, a sensitive and reliable measure of mobility[J].IEEE Trans Neural Syst Rehabil Eng,2010,18(3):303-310.

[9] Sejdic E,Lowry KA,Bellanca J,et al.A comprehensive assessment of gait accelerometry signals in time, frequency and time-frequency domains[J].IEEE Trans Neural Syst Rehabil Eng,2014,22(3):603-612.

[10] Stanković S,Orović I,Sejdić E.Multimedia signals and systems[M].New York:Springer,2012.

[11] Suthaharan S.Machine learning models and algorithms for big data classification[M].Boston:Springer,2016

[12] Peterson LE.K-nearest neighbor[J].Scholarpedia,2009,4(2):1883.

[13] Breiman L.Random forests[J].Mach Lear,2001,45(1):5-32.

[14] Komer B,Bergstra J,Eliasmith C.Hyperopt-sklearn: Automatic hyperparameter configuration for scikit-learn[J].Icml Automl Workshop,2014.

[15] Geurts P,Irrthum A,Wehenkel L.Supervised learning with decision tree-based methods in computational and systems biology[J].Mol Biosyst,2009,5(12):1593-1605.

[16] Arora S,Venkataraman V,Zhan A,et al.Detecting and monitoring the symptoms of Parkinson’s disease using smartphones: A pilot study[J].Park relat dis,2015,21(6):650-653.

[17] Lecun Y,Bengio Y,Hinton G.Deep learning[J].Nature,2015,521(7553):436