基于SOMP方法的分布式MIMO系统载波频偏估计

黄艳艳，彭华



基于SOMP方法的分布式MIMO系统载波频偏估计

黄艳艳，彭华

（信息工程大学信息系统工程学院，河南 郑州 450002）

首先根据高阶循环累积量的半不变性重新推导了信号和高阶循环累积量之间的关系式，然后利用SOMP方法联合重构出多个接收天线信号的高阶循环累积量，最后通过主要非零高阶循环累积量对应的循环频率和频偏的四倍关系，得到多个发送信号的频偏估计。与现有算法相比，所提算法充分利用接收信号间的相关性，提高了低信噪比下的多频偏估计性能，降低了导频数量。

分布式多输入多输出系统；多载波频偏估计；同步正交匹配追踪；联合重构

1 引言

分布式多输入多输出（MIMO, multiple input multiple output）系统是指基站端天线分布在相互间隔较远的地理位置，移动端也分布在不同地理位置的通信系统[1]。与基站端和移动端天线集中式放置的集中式MIMO系统相比，分布式MIMO系统的信道相关性更弱，能够获得更高的系统容量和小区覆盖率[2]，因此得到了广泛的关注。分布式MIMO系统中发送端和接收端之间频率振荡器的失配，使系统中存在多个载波频偏，影响系统性能，需要采取有效的多频偏估计算法对多频偏进行估计。

文献[3]给出了平坦衰落信道下多频偏估计的最大似然（ML, maximum likelihood）估计算法。该算法通过对接收信号的多维频偏信道似然函数进行多维联合最优化，从而得到多频偏。但是多维频偏信道似然函数的维度会随着收发天线数的增加呈指数级增加，算法复杂度较高。文献[4]给出了一种基于相关的多频偏估计算法。该算法在发送端布置多个相互正交的导频，并在接收端将某个发送信号对应的导频与接收信号做相关运算，得到信号的频偏估计。该算法将多维搜索简化为多个一维搜索，降低了文献[3]的算法复杂度，但该算法存在误差平台，即当信噪比大于一定值时，估计性能无法得到显著改善。文献[5]采用多重信号分类（MUSIC, multiple signal classification）和ML方法估计多频偏。相比于文献[3-4]，该方法降低了算法复杂度，避免了误差平台的产生。但是随着收发天线数的增加，信号间的相互干扰增强，算法性能下降。此外，上述文献需要大量的导频符号来得到高精度的频偏估计，降低了系统的频谱利用率。

文献[6]提出了一种多尺度多时延（MSML, multi-scale multi-lag）的水声信道模型，采用修正的粒子群优化（MPSO, modified particle swarm optimization）算法对水声信道的多普勒尺度因子、时延和幅度等参数进行估计。所提算法根据参数粒子当前的最优适应值不断迭代参数粒子的位置和速度，得到参数的局部最优值，并能同时得到所有路径上的参数。相比于传统的匹配追踪算法和分数傅里叶变换算法，所提算法具有更好的信道参数估计性能。文献[7]以最大化能效为目标，对大规模多输入多输出频分双工（MIMO FDD, multiple input multiple output frequency division duplexing）下行系统的信道估计和数据传输这2个阶段的资源分配问题，提出一种能效资源分配算法。

本文针对分布式MIMO系统，利用信号高阶循环累积量在循环频率域的稀疏特性，提出了一种基于分布式压缩感知（DCS, distributed compressive sensing）[8-10]理论的多频偏估计算法。所提算法根据高阶循环累积量的半不变性引入对角线投影等矩阵运算，重新推导了接收信号与高阶循环累积量之间的表达式。利用同步正交匹配追踪（SOMP, simultaneous orthogonal matching pursuit）[11-12]算法联合重构所有接收天线上的高阶循环统计量，根据主要非零高阶循环累积量对应的循环频率和载波频偏的四倍关系，得到多个发送信号的频偏。该算法能够在接收天线数增加的情况下提高重构成功率和低信噪比下的频偏估计性能，同时降低导频数量，提高频谱利用率。

2 信号模型

3 基于SOMP方法的多频偏估计

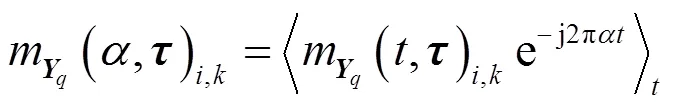
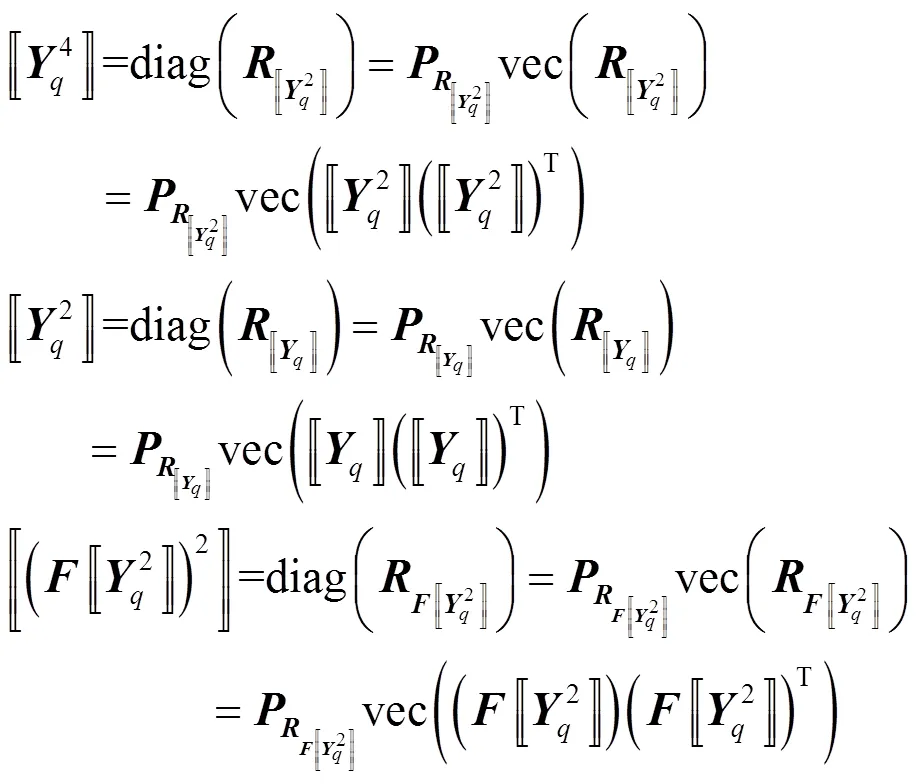
则有

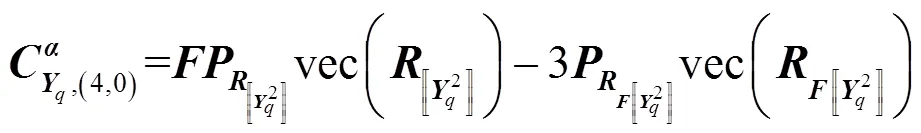
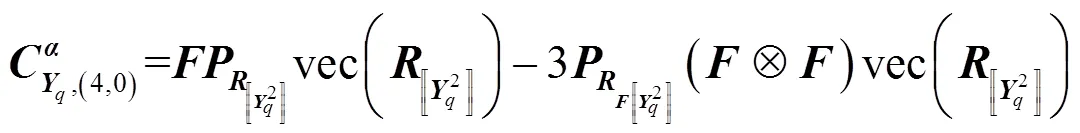
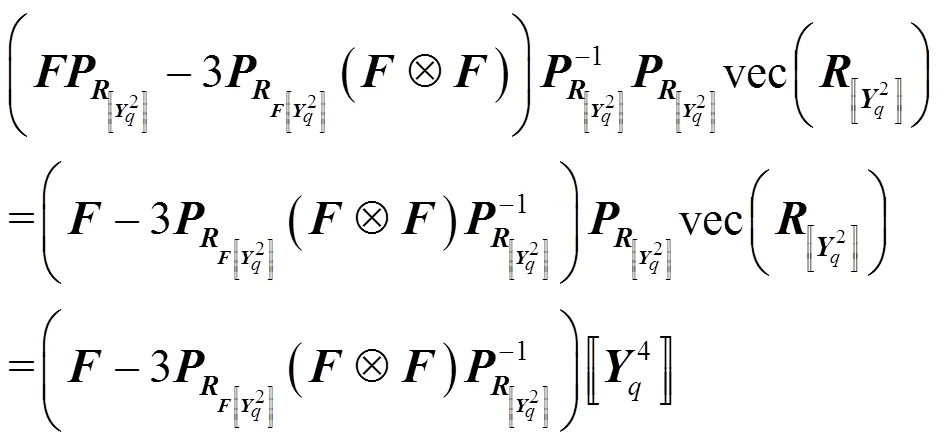
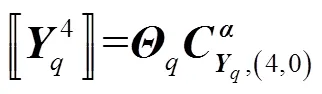
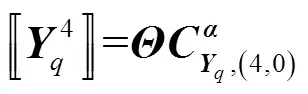
其中，有

(17)

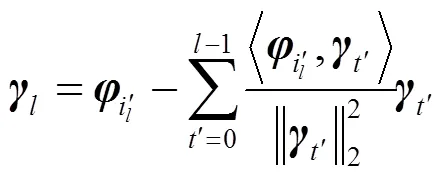
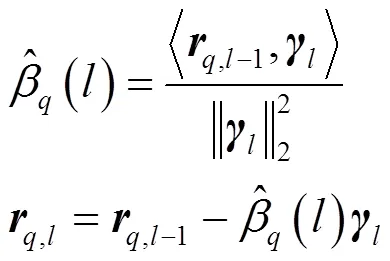
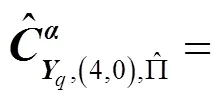
表1 估计范围、复杂度比较

4 仿真实验

实验1 考察本文算法与文献[4-5]算法的频偏估计性能。文献[4]是Yao算法，文献[5]是联合MUSIC+ML算法。图1给出了本文算法与文献[4-5]算法频偏估计的均方误差随信噪比变化的曲线。

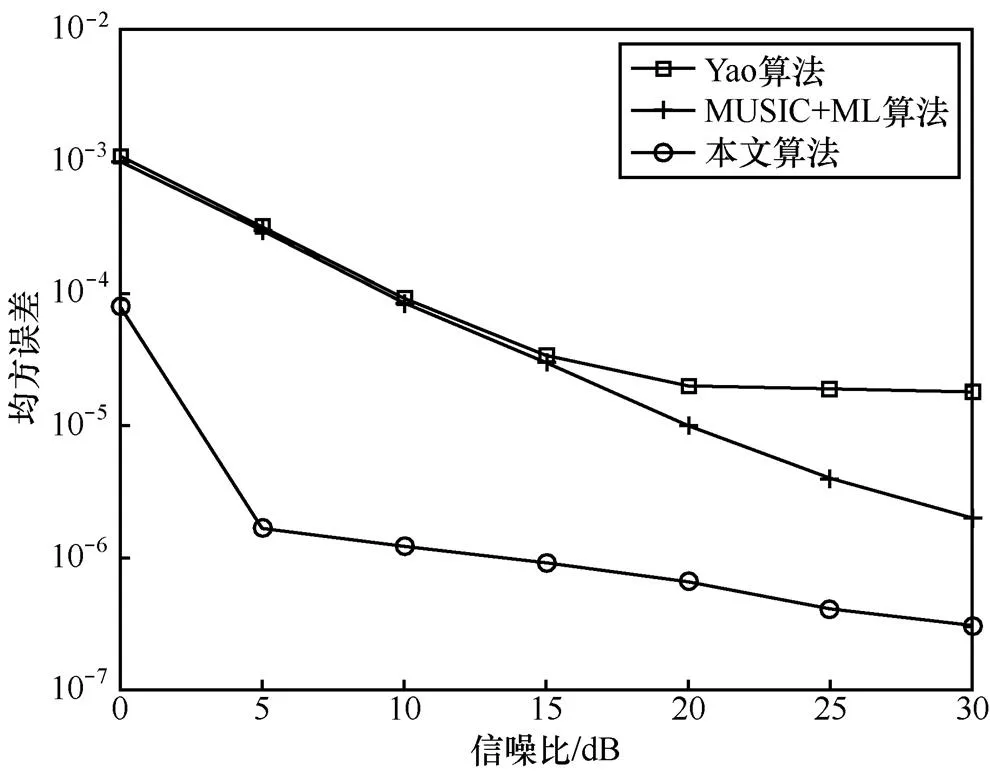
图1 频偏估计的均方误差随信噪比变化的曲线

由图1可知，本文算法在低信噪比下的性能明显优于文献[4-5]算法，且避免了文献[4]在中高信噪比下的误差平台。本文算法通过在循环频率域上精细搜索得到频偏估计值，并利用了高阶累积量在循环频率域上的稀疏特性，高阶累积量具有较好的抗噪性，因此所提算法在低信噪比下的性能较好；而文献[4]则是将正交性导频与接收信号进行相关运算，在低信噪比下导频正交性易被破坏，算法性能较差；文献[5]利用噪声子空间和信号子空间的正交性进行频偏估计，低信噪比下正交性易被破坏，算法性能较差。

在中高信噪比下，本文算法充分利用了信号间的相关性，随着信噪比的提高和接收天线数的增加，联合重构循环累积量的概率增大，频偏估计性能提高；文献[4]中信号间干扰无法随着信噪比的增加而减小，因此该算法具有误差平台；文献[5]中信号子空间和噪声子空间的正交性显著，但随着收发天线数的增加，信号间干扰变强，算法性能提升有限。

表2给出了文献[4-5]和本文算法的性能比较。

表2 性能比较

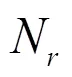
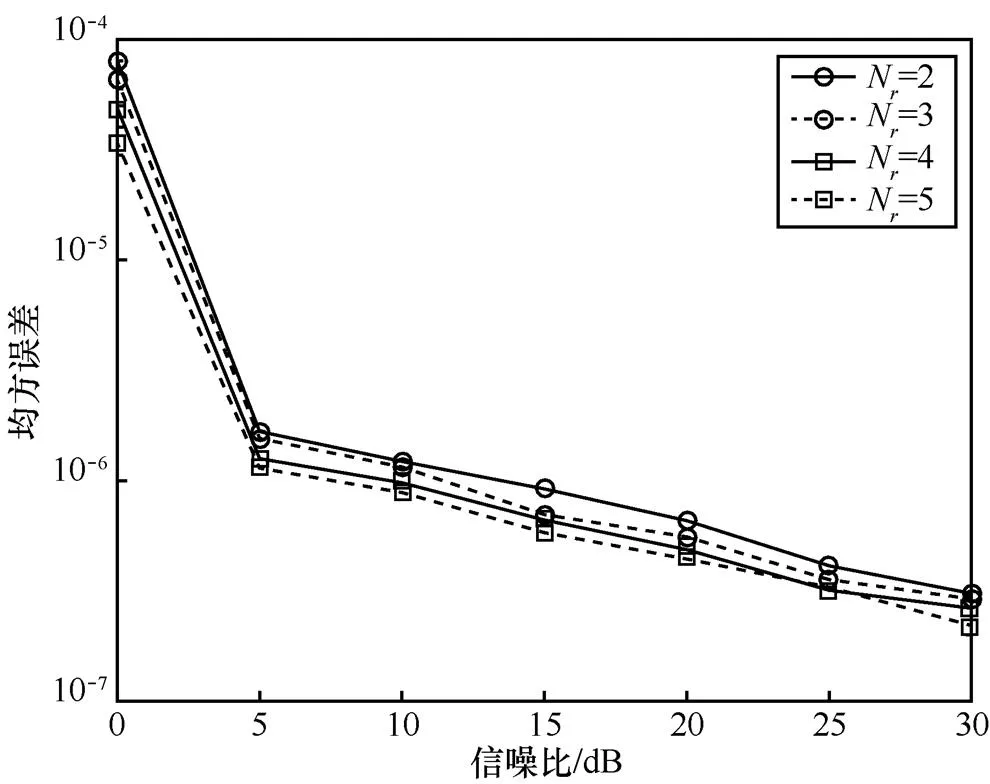
图2 不同接收天线数下的频偏估计性能曲线

由图2可以看出，随着接收天线数和信噪比的增加，本文算法的频偏估计性能有所提高。这是因为本文算法能够充分利用多个接收天线信号间的相关性，且随着接收天线数的增加，算法的重构成功率得到了提高，频偏估计性能得到提升。

实验3 考察本文算法所需的导频数。此时信噪比为10 dB，数据长度为[128,512]，接收天线数分别为2、3、4、5。图3给出了不同导频数据量下的频偏估计性能曲线。

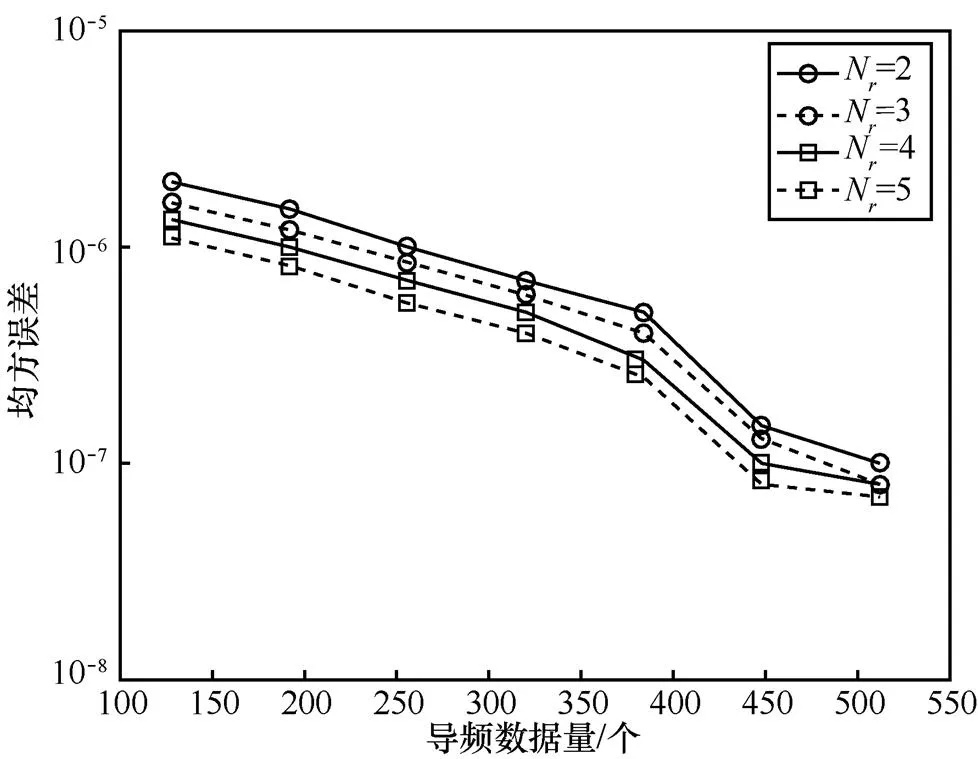
图3 不同导频数据量下的频偏估计性能曲线

从图3可以看出，随着接收天线数的增加，当频偏估计的均方误差为10−5时，算法所需的导频数变少，这是因为本文算法可以充分利用信号间的相关性，降低了达到某一性能时所需的导频数。

图4 不同下的频偏估计性能

5 结束语

针对现有基于导频的频偏估计方法估计精度有待进一步提高的问题，本文提出了一种基于分布式压缩感知的分布式MIMO系统频率估计方法。对于多个调制信号来说，高阶循环统计量在循环频率上具有稀疏特性，可用于辨识各个信号及其频率。但直接利用信号的高阶循环统计量进行频偏估计，算法的运算量较大。为了提高频偏估计精度，同时减少算法运算量，本文算法对多个接收天线上的信号进行联合观测，建立高阶循环统计量和观测数据的关系，利用SOMP方法联合重构所有接收天线上的高阶循环统计量，得到相应循环频率上的频率估计值。本文算法相比ML算法，将多维搜索问题转化为一维搜索问题，降低了算法的复杂度；相比Yao算法，则有更大的频偏估计范围，避免了误差平台的发生，能够提高低信噪比下的估计性能；相比MUSIC算法，能够提高低信噪比下的估计性能。随着接收天线数和待估参数的增加，本文算法能够充分利用信号间的相关性，降低在多接收天线下频偏估计的工作量，提高频偏估计性能。

[1] 何春龙, 任红, 郑福春, 等. 分布式天线系统:资源分配与能效优化[J]. 信息科学: 中国科学, 2017, 47(5): 591-606. HE C L, REN H, ZHENG F C, et al. Distributed antenna systems: resource allocation and energy efficiency optimization[J]. Information Science: Science China, 2017, 47(5): 591-606.

[2] 王清. 多小区和大规模分布式天线技术研究[D]. 济南: 山东大学, 2016. WANG Q. Research on multicell and massively distributed antenna techniques[D]. Jinan: Shandong University, 2016.

[3] BESSON O, STOICA P. On parameter estimation of MIMO flat-fading channels with frequency offsets[J]. IEEE Transactions on Signal Processing, 2003, 51(3): 602-613.

[4] YAO Y, NG T S. Correlation-based frequency offset estimation in MIMO system[C]//IEEE Vehicular Technology Conference. 2003: 438-442.

[5] 董伟, 李建东, 吕卓, 等. 基于MUSIC和ML方法的MIMO系统参数估计[J]. 电子与信息学报, 2008, 30(7): 1552-1556. DONG W, LI J D, LV Z, et al. Parameter estimation for MIMO system based on MUSIC and ML methods[J]. Journal of Electronics &Information Technology, 2008, 30(7):1552-1556.

[6] ZHANG X, SONG K, LI C G, et alParameter estimation for multi-scale multi-lag underwater acoustic channels based on modified particle swarm optimization algorithm[J].IEEE Access, 2017, 5: 4808-4820.

[7] WANG Y, LI C G, HUANG Y M, et al. Energy-efficient optimization for downlink massive MIMO FDD systems with transmit-side channel correlation[J]. IEEE Transactions on Vehicular Technology, 2016, 65(9): 7228-7243.

[8] BARON D, DUARTE M F, WAKIN M B, et al. Distributed compressive sensing[C]//IEEE International Conference on Acoustics Speech and Signal Processing. 2009: 2886-2889.

[9] PALANGI H, WARD R, DENG L. Distributed compressive sensing: a deep learning approach[J]. IEEE Transactions on Signal Processing, 2016, 64(17): 4504-4518.

[10] 周跃海, 吴燕艺, 陈东升, 等. 采用时域联合稀疏恢复的多输入多输出水声信道压缩感知估计[J]. 电子与信息学报, 2016, 38(8): 1920-1927. ZHOU Y H, WU Y Y, CHEN D S, et al. Compressed sensing estimation of underwater acoustic MIMO channels based on temporal joint sparse recovery[J]. Journal of Electronics & Information Technology, 2016, 38(8): 1920-1927.

[11] DETERME J F, LOUVEAUX J, JACQUES L, et al. On the noise robustness of simultaneous orthogonal matching pursuit[J]. IEEE Transactions on Signal Processing, 2017, 65(4): 864-875.

[12] JIN S, ZHANG X. Decentralized iterative reweighted algorithm for recovery of jointly sparse signals[C]//IEEE Wireless Communications and Networking Conference. 2015: 2109-2114.

[13] GARDNER W A, BROWN W A, CHEN C K. Spectral correlation of modulated signals: Part II-digital modulation[J]. IEEE Transactions on Communications, 1987, 35(6): 595-601.

[14] XIE L J ,WAN Q. Cyclic feature-based modulation recognition using compressive sensing[J]. IEEE Wireless Communications Letters, 2017, 6(3): 402-405.

[15] PUNCHIHEWA A, ZHANG Q, DOBRE O A, et al. On the cyclostationarity of OFDM and single carrier linearly digitally modulated signals in time dispersive channels: theoretical developments and application[J]. IEEE Transactions on Wireless Communications, 2010, 9(8): 2588-2599.

[16] BI D J, XIE Y L, LI X F, et alA sparsity basis selection method for compressed sensing[J]. IEEE Signal Processing Letters, 2015, 22(10): 1738-1742.

[17] TEMLYAKOV V N. Nonlinear methods of approximation[J]. Foundations of Computational Mathematics, 2003, 3(1): 33-107.

[18] TSAI Y R, HUANG H Y, CHEN Y C, et al. Simultaneous multiple carrier frequency offsets estimation for coordinated multi-point transmission in OFDM systems[J]. IEEE Transactions on Wireless Communications, 2013, 12(9): 4558-4568.

Carrier frequency offsets estimation for distributed MIMO system based on SOMP method

HUANG Yanyan , PENG Hua

Information System Engineering College, Information Engineering University, Zhengzhou 450002, China

By utilizing the half invariant property of high-order cyclic cumulants, the equation of signals and its high-order cyclic cumulants was rederivated first. Then simultaneous orthogonal matching pursuit (SOMP) method was used to jointly reconstruct multiple receiving signals’ high-order cyclic cumulants. At last, according to the fourfold relationship between carrier frequency offsets and cyclic frequencies of main non-zeros high-order cyclic cumulants, multiple transmitting signals’ carrier frequency offsets were obtained. Comparing with existing algorithms, the correlation between receiving signals is fully used by the proposed algorithm, the carrier frequency offset estimation performance at low signal to noise is improved and the pilots numbers are reduced.

distributed multiple input multiple output system，multiple carrier frequency offsets estimation, simultaneous orthogonal matching pursuit, jointly reconstruction

TN911.7

A

10.11959/j.issn.1000−436x.2018142

黄艳艳（1986−），女，浙江乐清人，信息工程大学博士生，主要研究方向为分布式MIMO系统的同步与均衡技术等。

彭华（1973−），男，江西萍乡人，博士，信息工程大学教授、博士生导师，主要研究方向为软件无线电和通信信号处理。

2017−10−19；

2018−07−16

黄艳艳，18638575039@163.com

国家自然科学基金资助项目（No. 61401511）

The National Natural Science Foundation of China (No. 61401511)