基于特征值的可验证特殊门限秘密共享方案

张艳硕，李文敬，陈雷，毕伟，杨涛



基于特征值的可验证特殊门限秘密共享方案

张艳硕1,2，李文敬1,2，陈雷1，毕伟3，杨涛2

（1. 北京电子科技学院密码科学与技术，北京 100070；2.公安部第三研究所，上海 201204； 3. 中思博安科技（北京）有限公司科学研究院，北京 100195）

秘密共享；特征值；可验证；黑盒子

1 引言

秘密共享技术已成为应用密码学中的一项重要技术，它在信息安全存储、传输以及安全计算等环节起着非常关键的作用。在秘密共享技术中最常见的是门限方案，已提出的门限方案有很多种，主要代表为Shamir[1]的Lagrange插值多项式方案、Blakley[2]的矢量方案、Asmuth等[3]的同余类方案及Karnin等[4]的矩阵法方案，这些方案已经得到了广泛的研究，但大多没有解决参与者行骗和密钥分发者欺骗的问题。为了解决上述问题，文献[5]提出了可验证秘密共享的思想，并给出了完整的实现方案。文献[6-8]提出了可抵抗恶意欺骗的秘密共享方案。文献[9-13]提出了可抵抗恶意欺骗的多秘密共享方案。

本文在基本Shamir门限方案的基础上，利用阶矩阵的特征方程具有重根的特点，提出了一种基于特征值的安全可验证的门限秘密共享方案。本文方案从矩阵特征值的角度出发，设计了一种可验证的秘密共享方案，这是本文方案的主要贡献。经分析证明，该方案是安全的，可以抵抗恶意欺诈。

2 基本Shamir门限秘密共享方案

1979年，Shamir[1]基于多项式的Lagrange插值公式提出了一个(,)门限方案，称为Shamir门限方案或Lagrange插值法。Shamir门限方案的详细介绍如下。

1) 参数选取

设()是有限域（为素数，且>），共享密钥为。有个参与者，要求重构该共享密钥至少需要个人。

2) 秘密分割

首先，密钥分发者独立随机地选择-1个元素1,2,…,a1Î()，构造一个-1次多项式为

最后，密钥分发者将个数对(x,y)，1≤≤，分别秘密传送给参与者1,2,…,，多项式()则是保密的，可以销毁。

3）秘密恢复

假设个参与者中的任意个（不妨设为1,2,…,T）准备一起恢复密钥。

首先，参与者出示他们的子密钥后，得到个点对(1,1)，(2,2)，…，(x,y)。

其次，个人计算多项式

最后，取多项式()的常数项(0)，即为所求的密钥。

3 （n1+n2+…+nt , 1+1+…+1）特殊门限秘密共享方案

在给出本文方案之前，我们先看（,+1）门限方案。文献[14]以某银行3位出纳和2位主任（正、副）开启保险库为例，为防止出现职员监守自盗、遗忘密钥或因职员缺席而打不开保险库等各种问题，银行规定至少有2位出纳和1位主任在场才能开启保险库，这样共有3×2=6种开启方式。本例中，由于出纳与主任的访问权限不同，定义了(,+1)门限方案。

定义1[14]设、为2个参与者的集合，∩（为空集），|，|，为门限值且<。假设共享密钥为，集合中的参与者A的子秘密为k(=1,2,…,)，集合中的参与者B的子秘密为k(=1,2,…,)。集合中不少于个参与者和中的一个参与者在一起可以恢复密钥，而其他任意组合方式都不能恢复密钥，称该方案为(,+ 1)门限共享方案。

在上述方案的基础上，本文提出一种特例。3家银行1、2和3共同管理一项基金，基金的使用需要征求3家银行执行董事的意见。其中，银行1有3个执行董事，银行2有4个执行董事，银行3有3个执行董事，每个执行董事都有一把钥匙。在这个例子中，3家银行均只需派出任意一位执行董事，即可决定该基金的使用状况，此时一共有3×4×3=36种决定方式。由此，本文定义了一种新的(1+2+…+n,1+1+…+1)门限秘密共享方案。

定义2 设1,2,…,B是个参与者的集合，任意2个集合的交集是空集，即B∩B=(1≤≤, 1≤≤,), |1|=1, |2|=2, …, |B|=n(1+2+…+n=)。每个集合的参与者均分得一个子密钥。主密钥恢复阶段，每个集合至少都出一个人，才可以计算出密钥，缺少任何一个集合的参与者都不能计算出密钥，则称这种方案为(1+2+…+n,1+1+…+1)特殊门限秘密共享方案。

4 特殊门限秘密共享方案

4.1 预备知识

4.1.1 方阵的特征值和特征向量

式(3)也可写成

这是个未知数个方程的齐次线性方程组[15]。

4.1.2 对称矩阵的性质

4.1.3 黑盒子

1) 黑盒子的定义

基于“黑盒子”[16]的含义给出其在本文方案中的定义。

2) 黑盒子的原理

①子密钥生成阶段是根据式(5)设计的，即

②主密钥恢复阶段，是根据式(3)设计的，即

3) 算例

以下用一个小例子说明黑盒子在本文方案中的用法。

子密钥生成阶段，主要功能程序如下。

①密钥分发者输入共享主密钥、集合的总个数和各集合的人数n：

=input('请输入要分发的秘密:');

=input('请输入集合的个数:') ;

for=1:

n=input('所对应的集合的人数:') ;

end for

②生成2阶随机可逆矩阵为

=rand(2,2);

for=1:

x=x(1,)

fprintf('%d',x)

n=input('所对应的集合的人数:') ;

for=1:−1

()=()=+(1,)(^());

(x)=(x)+(1,)(x^());

end for

for=1:n

for=1:2

E=[Emod((x),)];

end for

end for

end for

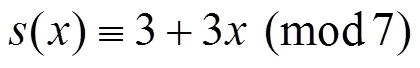
黑盒子生成的随机可逆矩阵为

生成的矩阵为

主密钥恢复阶段，主要功能程序如下。

①判断线性相关性

L=[ ] ;

P=[ ] ;

for=1:2

p=input('输入子秘钥:') ;

=p'··p

P=[Pp]

=[]

end for

=size(P);

=rank(P);

if(>)

fprintf('线性相关，停止恢复主密钥 ')

else

fprintf('线性无关，继续恢复主密钥 ')

end if

if((1,1)==(1,2))

fprintf('特征值相同，继续恢复主密钥 ')

else

fprintf('特征值不同，停止恢复主密钥 ')

当参与者输入正确的子密钥为

黑盒子输出：线性无关，继续恢复主密钥；

特征值相同，继续恢复主密钥；

λ=6；

当参与者输入伪造的子密钥为

黑盒子输出：线性无关，继续恢复主密钥；

特征值不同，停止恢复主密钥；

当参与者输入伪造的子密钥为

黑盒子输出：线性相关，停止恢复主密钥；

end if

4.2 方案设计

本节将给出具体方案，该方案可分为4个步骤：系统描述、参数选取、秘密分割以及秘密恢复。

4.2.1 系统描述

4.2.2 参数选取

系统参数的选取是为了给后续工作做准备。

4.2.3 秘密分割

4.2.4 秘密恢复

本文方案要求恢复秘密参与者的人数不少于门限值，即每个参与者集合必须至少出一个人。

①λ=λ=λ1。

只有同时满足上述2个条件才可以进行下一步操作，否则，停止密钥恢复工作。

5 方案分析

从正确性、完善安全性和欺诈检测这3个方面来分析本文方案。

5.1 正确性证明

命题1 在参与者诚实而正确地执行方案的前提下，任意合法的授权子集都可以恢复密钥。

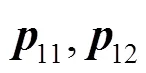
实质上，本文方案的正确性是建立在Shamir门限方案正确性的基础上的。

5.2 完善安全性证明

命题2 当中参与者总数不够时，无法恢复密钥。

5.3 欺诈检测

5.3.1 检验密钥分发者是否可靠

命题3 各参与者在收到子秘密之后，可通过式(3)检验密钥分发者是否可靠。

5.3.2 检测参与者是否诚实

命题4 在秘密恢复阶段，也可通过式(3)检验参与者是否诚实。

6 方案的具体应用

下面用一个例子说明本文方案的可行性。

例 设有1、2这2个集合，集合1中有一个参与者11，集合2中有一个参与者21。为这2个用户分配密钥，并分析重构密钥的过程。

1) 参数选取

2) 秘密分割

密钥分发者取1=(1)=(3)=2，2=(2)=(6)=1。

得到对角矩阵为

3) 秘密恢复

所以，有

所以=3，从而获得共享密钥。

7 结束语

本文提出了一种基于特征值的可验证的特殊门限秘密共享方案。方案中的每个参与者需持有2种子密钥，其优点是可以有效地保证密钥分发者分发子密钥的真实性和参与者提供子密钥的真实性。同时，本文方案利用黑盒子的设计理念，使方案的密钥分发者和参与者可以进行互相认证，实现了防欺诈功能。本文方案的贡献还在于，从特征值的角度出发设计了一种可验证的秘密共享方案。

[1] SHAMIR A. How to share a secret[J]. Communication ACM, 1979, 22(11): 612-613.

[2] BLAKLEY G R. Safeguarding cryptographic keys[C]//IEEE Computer Society. 1979: 313.

[3] ASMUTH C, BLOOM J. A modular approach to key safeguarding[J]. IEEE Transactions on Information Theory, 1983, 29(2):208-210.

[4] KARNIN E D, GREENE J, HELLMAN M E. On secret sharing systems[J]. IEEE Transactions on Information Theory, 1983, 29(1):35-41.

[5] CHOR B, GOLDWASSER S, MICALI S, et al. Verifiable secret sharing and achieving simultaneity in the presence of faults[C]// Symposium on Foundations of Computer Science.2008:383-395.

[6] LIU C J, LI Z H, BAI C M, et al. Quantum-secret-sharing scheme based on local distinguishability of orthogonal seven-qudit entangled states[J]. International Journal of Theoretical Physics, 2018, 57(3):1-15.

[7] XU T T, LI Z H, BAI C M, et al. A new improving quantum secret sharing scheme[J]. International Journal of Theoretical Physics, 2017, 56:1-10.

[8] SINGH N, TENTU A N, BASIT A, et al. Sequential secret sharing scheme based on Chinese remainder theorem[C]// IEEE International Conference on Computational Intelligence and Computing Research. 2017:1-6.

[9] SONG Y, LI Y, WANG W. Multiparty quantum direct secret sharing of classical information with bell states and bell measurements[J]. International Journal of Theoretical Physics, 2018, 57(5):1559-1571.

[10] PILARAM H, EGHLIDOS T, PILARAM H, et al. A lattice-based changeable threshold multi-secret sharing scheme and its application to threshold cryptography[J]. Scientia Iranica, 2017, 24(3):1448-1457.

[11] BASIT A, KUMAR N C, VENKAIAH V C, et al. Multi-stage multi-secret sharing scheme for hierarchical access structure[C]//International Conference on Computing, Communication and Automation. 2017:556-563.

[12] ZHANG T, KE X, LIU Y. (,) multi-secret sharing scheme extended from Harn-Hsu’s scheme[J]. Eurasip Journal on Wireless Communications & Networking, 2018, 2018(1):71.

[13] YUAN D, HE M, ZENG S, et al. (,)-threshold point function secret sharing scheme based on polynomial interpolation and its application[C]//IEEE/ACM International Conference on Utility and Cloud Computing. 2017:269-275.

[14] 李滨. 基于特殊访问权限的差分秘密共享方案[J]. 四川大学学报(自然科学版), 2006(1): 78-83.

LI B. Differential secret sharing scheme based on special access permissions[J]. Journal of Sichuan University (Natural Science Edition), 2006(1): 78-83.

[15] 同济大学数学系编.工程数学线性代数[M]. 北京: 高等教育出版社, 2014. School of Mathematic Sciences, Tongji University . Engineering mathematics, linear algebra[M]. Beijing: Higher Education Press. 2014.

[16] 曹尔强, 张沂, 曹晔, 等. “软件黑盒子”文件加锁和加密的一个方法[J]. 长春邮电学院学报,1991(3):11-14. CAO E Q, ZHANG Y, CAO Y ,et al. A technique of locking a disk and secreting a whole disk[J]. Journal of Changchun Post & Telecommunication Institute, 1991(3):11-14.

Verifiable special threshold secret sharing scheme based on eigenvalue

ZHANG Yanshuo1,2, LI Wenjing1,2, CHEN Lei1, BI Wei3, YANG Tao2

1. Department of Cryptography Science and Technology, Beijing Electronic Science and Technology Institute, Beijing 100070, China 2. The Third Research Institute of Ministry of Public Security, Shanghai 201204, China 3. Institute of Science, Zsbatech Corporation, Beijing 100195, China

secret sharing, eigenvalue, verifiable, black box

TP309

A

10.11959/j.issn.1000−436x.2018143

张艳硕（1979−），男，陕西宝鸡人，博士，北京电子科技学院讲师，主要研究方向为密码理论及其应用。

李文敬（1992−），女，山东济宁人，北京电子科技学院硕士生，主要研究方向为信息安全。

陈雷（1992−），男，河北邯郸人，北京电子科技学院硕士生，主要研究方向为信息安全。

毕伟（1980−），男，黑龙江哈尔滨人，博士，中思博安科技（北京）有限公司研究员，主要研究方向为信息安全和区块链技术。

杨涛（1977−），男，安徽芜湖人，博士，公安部第三研究所副研究员，主要研究方向为信息安全。

2018−01−25；

2018−06−22

信息网络安全公安部重点实验室开放基金资助项目（No.C17608）；中国民航信息技术科研基金资助项目（No.CAAC-ITRB-201705）；国家自然科学基金资助项目（No.61772047）

The Opening Project of Key Lab of Information Network Security of Ministry of Public Security (No.C17608) , The Information Technology Research Base of Civil Aviation Administration of China (No.CAAC-ITRB-201705), The National Natural Science Foundation of China (No. 61772047)