基于VMD和形态差值滤波器的特征提取算法*

艾澍海， 张寿明

(昆明理工大学 信息工程与自动化学院，云南 昆明 650500)

0 引 言

轴承早期的故障信号比较微弱，并且噪声也很强，如何在复杂工况中有效提取滚动轴承早期的故障特征，及时发现并判断出故障的类型、部位，对于保障机械设备正常运行和减少经济损失具有重要的作用，也是当前研究的热点和难点课题。郝如江等人[1]设计了多尺度混合形态滤波器和形态闭开的差值滤波器用于故障信号的特征提取；蒋永华等人[2]利用最小Shannon 熵方法优化Morlet 小波的形状参数，对信号进行Morlet 小波变换实现故障特征的提取；张志刚等人[3]提出了一种基于改进经验模态分解(empirical mode decomposition,EMD)与谱峭度法的特征提取方法；王志坚等人[4]提出了基于最小熵反褶积和总体平均经验模态分解(ensemble EMD,EEMD)来提取微弱故障特征；王建国等人[5]采用自相关分析提取信号中的周期成分，消除噪声的干扰，再利用局域均值分解(local mean decomposition,LMD)进行振动信号故障特征提取，上述方法均取得了良好的效果，但均存在局限性。

相比于EMD,变分模态分解(variational mode decomposition，VMD)[6]具有更好的信噪分离效果，在抑制模态混叠方面优于EMD[7]和LMD[8]。形态差值滤波是形态学滤波器中效果较好的方法，具有算法简单，执行效率高的特点，能有效抑制信号中噪声和谐波成分，提取出正负冲击成分，方便在线实时监测，提取故障特征[9]。

本文将VMD和形态差值滤波器相结合进行故障特征提取。通过VMD得到若干模态分量，通过峭度准则计算得到峭度最大的信号分量;利用形态差值滤波器进一步抑制所得信号分量中的噪声成分;对提取的信号进行了Hilbert包络谱分析。实验结果分析表明了该方法的有效性和优越性。

1 VMD

1.1 VMD的基本原理

1)变分问题构造

调幅—调频信号

uk(t)=Ak(t)cosφk(t)

(1)

约束变分模型表达式

(2)

式中 {uk}={u1,…,uk}为分解的K个IMF分量,{ωk}={ω1,…,ωk}为各分量的频率中心。

2)变分问题求解

求解变分约束模型的最优解，利用二次罚函数项α和Lagrange乘子λ，获得扩展的Lagrange表达式如下

L({uk},{ωk},λ)∶=

(3)

(4)

(5)

1.2 VMD算法流程

2)循环n=n+1；

3)对所有的ω≥0，对k和ωk进行更新；

4)更新λ

(6)

2 形态学滤波

2.1 形态学滤波原理

形态学的基本运算主要有腐蚀、膨胀、形态开和形态闭运算。其中，f(n)关于g(n)开和闭运算分别定义为

(f∘g)(n)=(fΘg⊕g)(n)

(7)

(f·g)(n)=(fΘg⊕g)(n)

(8)

式中n∈{0,1,2,…,M-1}。

2.2 形态差值滤波器

形态开、闭运算是形态学的基本滤波器，分别可以平滑信号中的正向和负向脉冲[10]，由于滚动轴承的故障信号中常常同时包含正向脉冲和负向脉冲[11]，微弱的故障冲击成分也会经常被噪声所覆盖，需要同时使用形态开、闭运算的组合算法来进行分析，因此，选择形态差值滤波器，其表达式为

fDIF(n)=f·(n)-f∘(n)

(9)

可将式(9)分解为

f·g-f∘g=(f·g-f)+(f-f∘g)

(10)

式中f·g-f和f-f∘g分别为黑、白Top-hat变换，用于提取信号的负向和正向脉冲[12]。利用这两种变换的形态差值滤波器对于微弱信号的提取更加有效。

2.3 结构元素

结构元素的尺寸和形状决定着结构元素的特征，对于形态学滤波的效果有着重要的影响[13，14]。

选择扁平型的结构元素，其与滚动轴承故障信号特征形态比较接近，且能较好地分析信号特点，运算度较低。

3 特征提取方法流程

1)获取轴承内外圈振动信号，对信号进行VMD，得到本征模函数(intrinsic mode function,IMF)分量；

2)计算每个IMF分量峭度，根据峭度准则筛选得到故障特征最明显的IMF分量；

3)对步骤(2)中得到的信号用形态差值滤波器进行形态滤波处理，得到滤波后的时域图；

4)对步骤(3)中的信号进行Hilbert包络谱分析，提取信号特征信息；

5)将提取的信号与故障信号比较，判断故障的类别。

4 轴承故障实验分析

采用具有内外圈故障的滚动轴承作为研究对象。本文采用的是美国Case Western Reserve University滚动轴承故障测试中心提供的故障数据信号[15]，实验使用的轴承参数为滚动体径为7.94 mm,滚动轴承节径为39.04 mm,滚动体数为9.00个，接触角为0°， 轴承负载为2.23 kW，采样频率为48 kHz，采样长度为4 800 点；实验中，分别在内外圈加工出直径为 0.177 8 mm，深0.279 4 mm 的小槽模拟故障裂纹以获取故障信号数据。通过相关参数的计算，算得内外圈裂纹故障基频分别为156.14 Hz和103.36 Hz。

4.1 滚动轴承外圈故障特征提取

图1为外圈故障VMD后的频谱，通过原始信号频谱可以看出，原始信号中含有比较明显的故障冲击成分和比较多的噪声干扰，其振动频谱成分比较丰富，很难利用单一的方法来确定故障的类型。利用本文方法首先对外圈故障振动信号进行VMD处理，由图1知仍然存在很多噪声信号的干扰；根据峭度准则选取峭度最大的IMF1分量(峭度值为5.21)进行形态差值滤波，滤波后的信号时域图如图2所示，此时噪声基本滤除；对信号进行Hilbert包络谱分析，得到图3所示的外圈Hilbert包络谱，可以明显看出故障信号的1倍频(105.5 Hz)、2倍频(205.5 Hz)和3倍频(310.5 Hz)等各谐波频率，且有效地滤除了噪声，能够凸显出故障的特征，方便对比分析出故障的类型，证明了本文方法的有效性。

图1 外圈故障VMD后的频谱

图2 外圈形态差值滤波后的时域图

图3 外圈Hilbert包络谱分析

4.2 滚动轴承内圈故障特征提取

利用与外圈故障特征提取同样的方法，对于内圈故障信号，提取各过程结果如图4～图6所示，IMF分量峭度最大值为IMF2(5.18)。本文提出的方法能有效地提取出故障信号特征的1倍频(152.3 Hz)、2倍频(310.5 Hz)和3倍频(462.9 Hz)。

4.3 与传统方法对比

为了体现本文所用方法与传统分析方法的优越性，采用EEMD和差值滤波器相结合的方法与本文方法进行对比。对比实验结果如图7和图8所示。

从对比实验结果可以看出，EEMD方法受噪声影响比较大，提取出来的故障特征不明显，外圈故障特征只提取出了特征频率和2倍频，内圈故障只提取处理特征频率和 2倍频、3倍频，相比于本文的方法有着明显的不足。

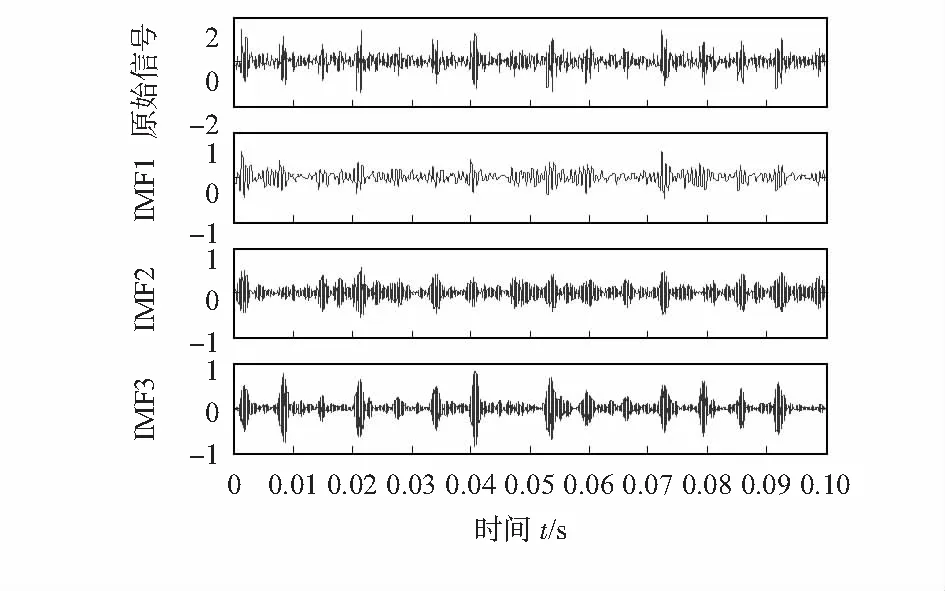
图4 内圈故障VMD后的频谱

图5 内圈形态差值滤波后的时域图

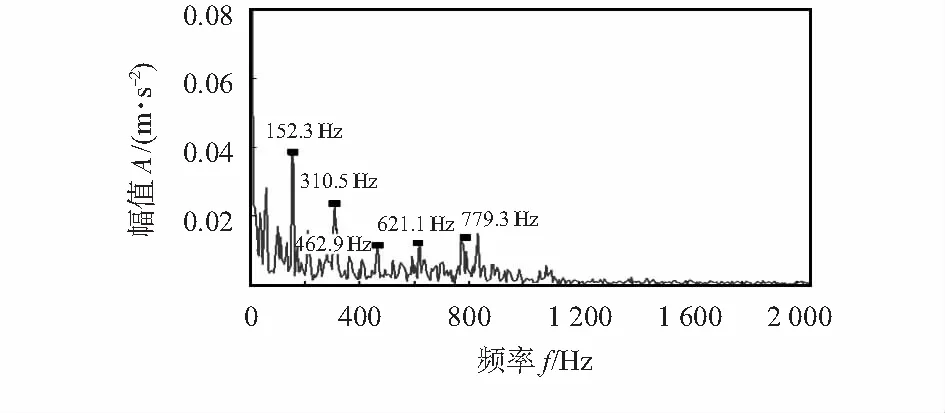
图6 内圈Hilbert包络谱分析

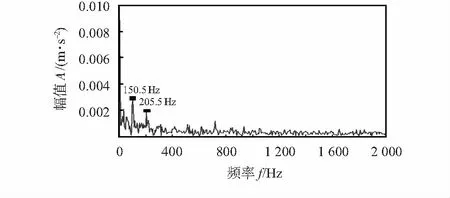
图7 对比方法外圈包络谱分析

图8 对比方法内圈包络谱分析

5 结 论

1)VMD能够有效地放大滚动轴承早期故障信号中微弱的冲击特征信息，便于判断滚动轴承的运行状态和进一步信号处理。

2)形态差值滤波器对VMD处理后故障信号进行滤波，能很好地过滤信号中的噪声成分，无需考虑振动信号的频谱特征与分布，即可有效提取出故障信号的频率特征。

3)通过与传统EEMD的比较表明，本文提出的方法，既能有效放大滚动轴承早期内圈外圈的微弱的特征信息，又能有效滤除故障信号噪声，可以很好地提取出信号特征，分析效果更好，优势明显。