联合Wilson方法与遗传算法的水平轴风力机叶片优化设计
王 昊, 陆 杨, 周 欢, 韩春辉
(上海电力学院 能源与机械工程学院, 上海 200090)
风能作为一种清洁、无污染的新型能源,对于解决能源危机和可持续发展起到了积极作用[1]。风力机叶片的气动性能决定了风能的转换效率,设计优良的叶片可以使风力机获得最大的风能利用系数和良好的运行寿命[2-3]。国内外用于风力机叶片优化设计中比较成熟的方法主要是基于叶素动量理论的Glauert方法、Schmitz方法和Wilson优化方法,而Wilson优化方法更加接近工程实际[4]。此外,遗传算法也是一种受到重视的优化方法。Wilson优化设计理论研究了叶尖损失和升阻比对叶片最佳性能的影响,并且研究了风轮在非设计状态下的性能[5]。该方法以额定风速下功率系数最大为优化目标,设计出来的叶片具有较高的风能利用率,而且模型较为简单,计算方便。但其设计结果需要大幅修正[6],修正后的叶片已经偏离了设计点,使设计效果难以控制。遗传算法作为一种高等优化算法,能较好地处理非线性约束和多目标优化问题[7]。由于只用编码和适应度来描述复杂问题,故不要求明确的数学方程和导数表达式。在风力机叶片优化设计中,可以加入弦长和扭转角约束方程,预给定叶片的气动布局,并能在优化目标的基础上快速得到叶片的最优布局,进行叶片弦长和扭角的优化搜索[8]。
目前,将Wilson方法与遗传算法相结合进行叶片优化的研究还很少。本文综合考虑了Wilson优化法与遗传算法各自的优点,并进行了较为合理的结合,希望能使优化后的叶片外形及其气动性能优于单独的两种方法。
1 叶片的联合优化设计基本思想
叶片优化设计中采用由Wilson方法所设计出来的叶片,叶片弦长为c,扭角为θ,c和θ均是非线性分布的,因此通常会进行线性修正。在修正后的弦长c的分布上,靠近叶根的部分仍然存在一些突变。修正后的扭角θ分布几乎呈现线性流线分布,但此时由Wilson方法得到的弦长c已经不再适用,因此需要对叶片进行再优化设计,重新优化弦长c。
考虑到遗传算法是随机全局搜索的优化方法[9],具有效率高、并行性好,以及可以全局搜索的特点,在搜索寻优的过程中可以自适应地控制搜索过程。因此,本文提出了一种联合优化设计方法,即将Wilson优化方法与遗传算法进行有效的结合。首先用Wilson方法优化设计叶片的气动外形,对优化结果仅进行扭角值的修正,然后将修正后的扭角加入到遗传算法中,通过改变微小范围搜索寻优,对叶片的弦长进行再次优化,最终得到叶片的气动外形。
2 叶片的联合优化设计数学模型和基本参数
2.1 Wilson方法
在水平轴风力机气动性能计算中,片条理论[10-11]是很重要的方法。其计算模型考虑了叶尖损失、轮毂损失、叶栅理论,以及失速状态下动量理论修正模型。经过修正后,可迭代求得轴向诱导因子a和切向诱导因子b,其表达式为
式中:B——叶片数;
CL,CD——翼型的升阻力系数;
φ——入流角;
F——叶尖损失系数;
r——叶片展向半径(局部半径);
U——来流风速;
Ω——风轮转速。
风轮所产生的功率P的计算公式为
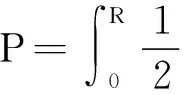
(4)
式中:R——风轮半径;
ρ——气流密度;
W——相对风速。
式(4)中的W满足
(5)
由式(3)和式(5)可得,相对风速W与来流风速U的关系式为
(6)
将式(6)代入式(4),并利用式(1)可得到不含诱导因子的功率表达式为
(7)
由式(7)可以看出,风力机的功率取决于相对风速、叶片数、弦长、入流角、风轮转速、翼型的升阻力系数,以及风轮半径等因素。
2.2 联合优化设计目标函数
考虑到遗传算法的运行速度以及结果的准确度,将叶片沿展长方向均分为7个截面,以叶片的风能利用系数CP最大为优化的目标函数。
风能利用系数CP的计算公式为[12]
(8)
以CP最大为目标函数,在进行风轮设计时,首先需要确定来流风速、风轮转速和风轮半径,这样风能利用系数CP就只依赖于叶片的功率。
由式(7)可以看出,叶片的功率值只与叶片弦长c和扭角θ值相关。因此,将式(8)作为目标函数,并且以弦长c和扭角θ为设计变量。
θ=φ-α
(9)
式中:α——攻角。
2.3 联合优化设计约束条件
根据本文所提出的联合优化设计思想,每个截面的扭角θ由Wilson方法优化并经过修正得到,在每一个截面对应的扭角θ已知的情况下重新搜索弦长c。由于此时的扭角是作为已知量给出的,那么对于叶片的设计变量可采用以下约束条件
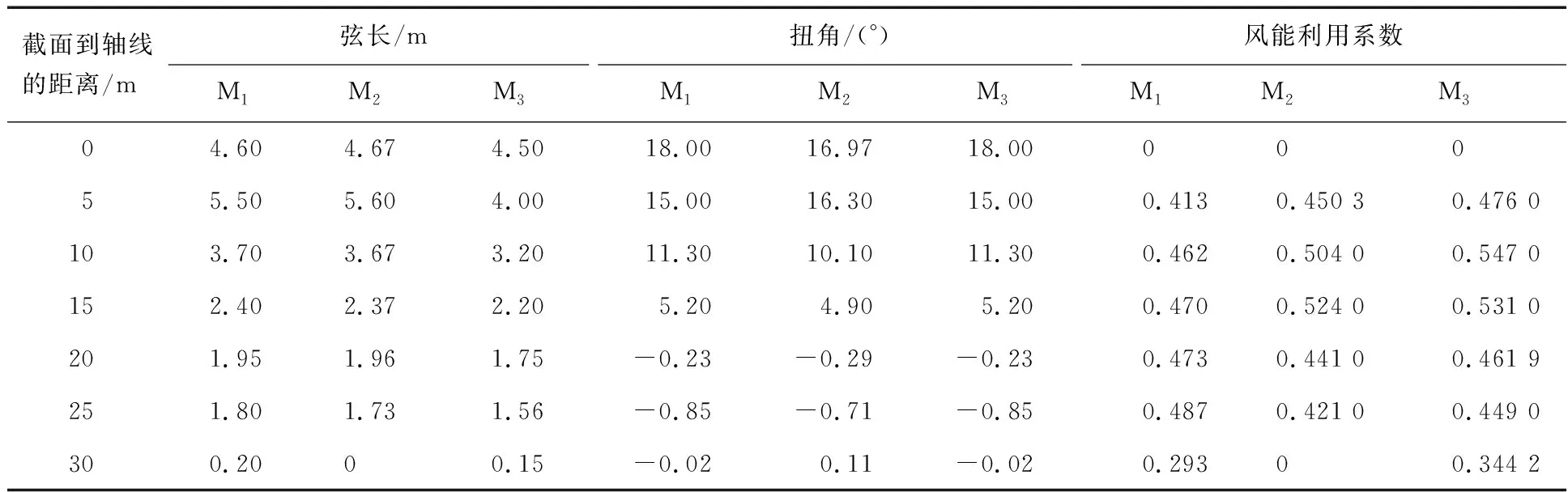
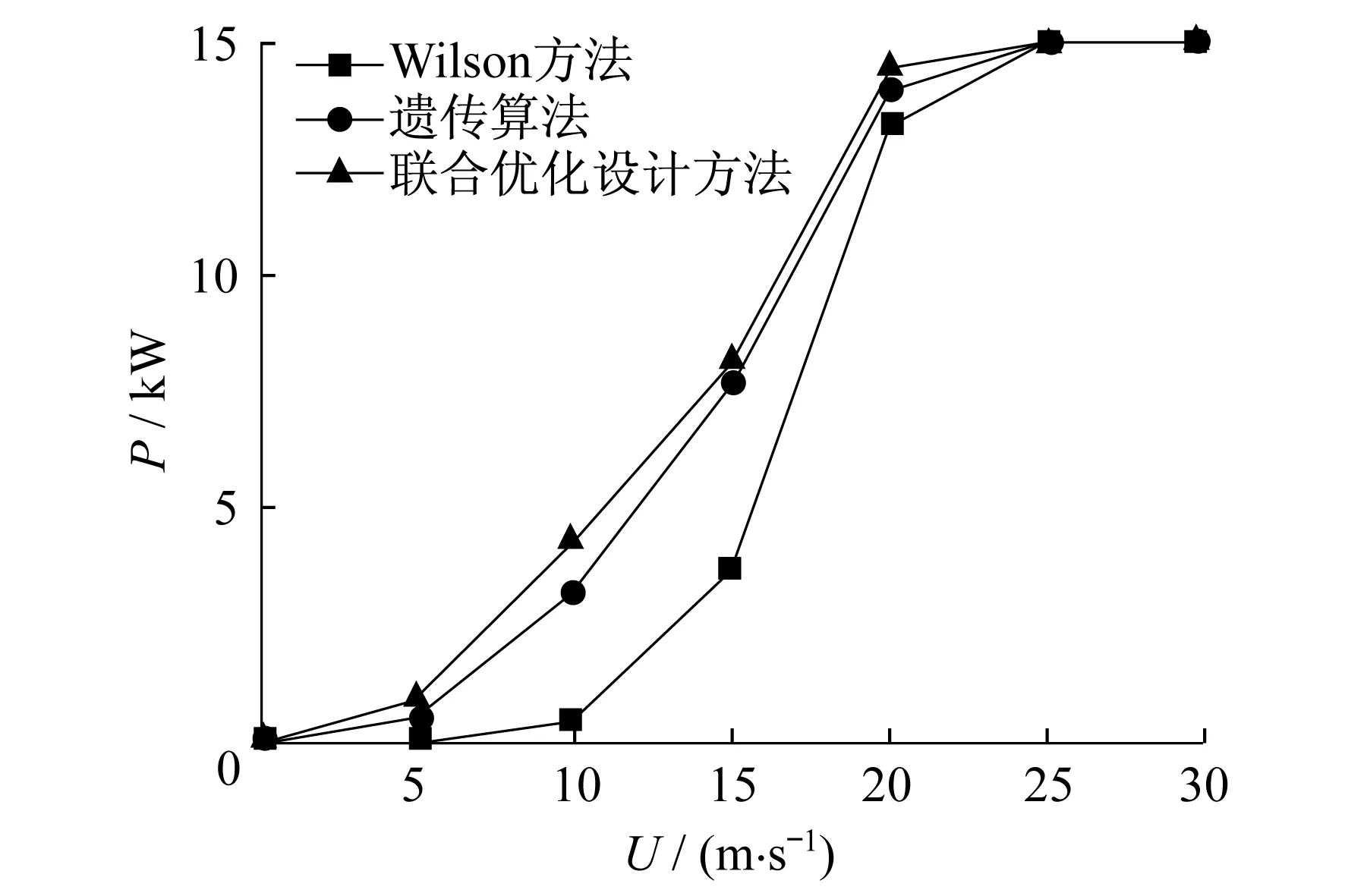
cmin 本文所确定的叶片基本参数数值如表1所示。 表1 叶片基本参数 为了验证联合优化设计方法的可行性和优越性,将Wilson优化方法(M1)、遗传算法(M2)和联合优化设计方法(M3)所得到的各个截面上的弦长、扭角和风能利用系数值的数据分布情况进行比较,分别如表2,图1,图2,图3所示。 表2 3种方法的数据对比 由表2和图1可以看出,采用Wilson方法和遗传算法所得到的弦长,在靠近叶根部分均呈现逐渐增加的趋势,随后逐渐减小,两种方法所得到的弦长分布趋势相同,且数值上变化甚微。但是遗传算法优越于Wilson方法的地方在于,其优化所得的结果不需要再进行修正。采用联合优化设计方法所得到的弦长,沿着叶展方向上整体呈现递减趋势。这样的变化趋势有利于叶片的工业加工,流线型的分布情况可以降低制造难度,并且弦长数值在整体上小于遗传算法和Wilson方法。 由于在进行联合优化设计的过程中保持了Wilson计算结果的扭角值,故在图2中没有给出Wilson方法的扭角分布。由表2和图2可以看出,3种方法所得到的扭角分布在叶展方向上均呈递减趋势,并且在叶根处的扭角值也相差较小。同时,由联合优化设计方法得到的扭角值线性特性要好于遗传算法,而线性性能越好,工艺过程越简单,制造及加工费用也就越低。 由表2和图3可以看出,3种方法所得到的风能利用系数在整个叶展方向上的数值均大于0.4,说明3种优化设计的结果均是可行的。联合优化设计方法的Cp值最大可达到0.547,遗传算法的Cp最大值为0.524,Wilson方法的Cp值最大为0.487。从图3的整体变化趋势上看,联合优化设计方法的结果在整体分布上高于遗传算法,遗传算法的结果高于Wilson优化。 图1 弦长分布对比示意 图2 扭角分布对比示意 图3 风能利用系数分布对比示意 图4为3种方法的气动性能功率变化曲线。由图4可以看出,在整个风速的变化范围内,联合优化设计方法所得到的结果要高于遗传算法,遗传算法高于Wilson方法。当风速为20 m/s时,采用联合优化设计方法所设计的风力机叶片的输出功率达到额定功率的96.21%,遗传算法设计的风力机叶片输出功率为额定功率的93.10%,而Wilson方法设计的叶片输出功率为额定功率的89%。通过上述的数据分析可以得出,联合优化设计方法是最优的方法,其次是遗传算法,最后是Wilson方法,经过优化设计后的风力机气动性能有较大的改善。 图4 功率随风速变化的曲线 本文提出了一种新的优化设计方法,即将Wilson方法与遗传算法相结合形成了联合优化设计方法。以风能利用系数Cp最大为目标函数,将Wilson方法所得到的扭角修正值作为遗传算法的输入量,对设计变量弦长进行重新搜索寻优,得到该优化方法下叶片的外形数据以及目标函数值。分别从叶片的外形数据到风能利用系数以及气动性能的计算结果3个方面,对3种方法进行比较,最终得到联合优化设计方法优于遗传算法和Wilson方法的结论,验证了本文优化设计方法的有效性和优越性。2.4 叶片的基本参数
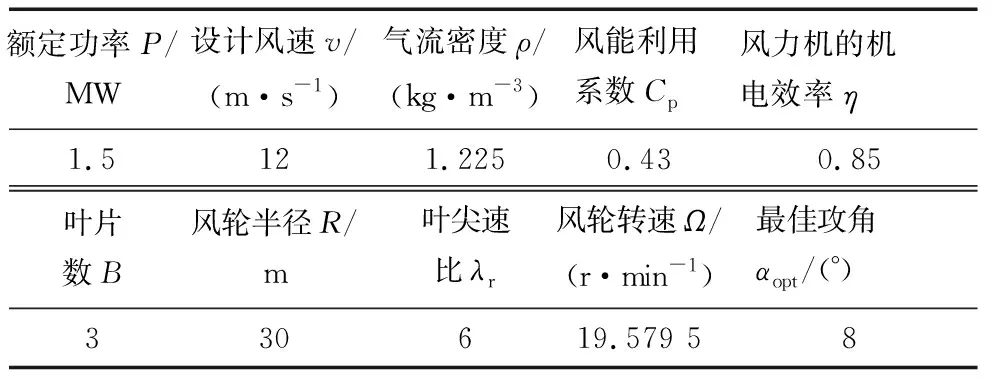
3 3种方法的对比分析



4 结 语

