基于因子分析法的教学质量评价模型

贾 珍 潘晓琳

(重庆师范大学数学与科学学院，重庆 401331)

自恢复高考以来，我国的教育教学水平得到了显著性的提升。尤其在21世纪，以提高人才质量为根本的教育教学改革的一项重要指标就是教学质量[1]。一直以来教学质量的优劣都是评定教育教学水平的标杆，是教学质量和办学效益得到提高的风向标。随着教育事业的平稳发展，各高等院校作为培养青年才俊的第一平台，目前虽然各自都有一套教学质量评价的相关制度体系、指标体系、监控体系以及考核体系，但是都是采用传统的教学质量评价方法。传统的教学质量评价法是由学生进行考评，该方法是学校教务处在特定时间段内将已拟定好的选项卡发放给学生，让学生根据卡片上的内容对教师教学水平进行评价，再经教务人员综合该教师各项得分而开展的。

传统的评价方法未对数据进行统计分析，只是对数据的简单堆积，更没有反馈机制，而且教学质量的评价需要考虑的因素很多，模糊评价方法对于指标间信息的冗余很难处理[2]。鉴于此，提出用因子分析法对原始指标进行筛选，通过建立综合评价模型以期找到一种比传统评价方法更为客观的评价方法。

1 评价指标体系的建立

不同阶段、不同类型的学校评价教学质量所侧重的指标有差异，因此评价指标体系的建立需要一个适用性良好的教学质量评价模型。指标的建立应满足全面性、可测性、科学性的原则。一般的评价指标会从教学态度、教学内容、教学方法、教学能力、教学效果等几个方面构建评价指标体系，会产生对某几项指标的反复使用与评价，造成评价主体因角度不同，而出现结果相悖的现象。因此在构建指标体系时，学生评价应侧重于教师的课堂教学，院系专家评价应侧重于以课堂教学为中心的教学环节上的各关键点。这样，评价结果既覆盖全面又各有侧重，会更具有可信度[3]。

为了适应现代教育的发展，着眼于高校管理过程中对教学质量的评价，结合学校已有的评价体系，采用定性定量分析，建立教学质量评价指标体系。在广泛查阅资料、文献的基础之上力求使评价结果详实、充分地反映当前的教学质量水平。该指标体系有一级指标5个，二级指标25个。具体评价指标体系结构见图1。

2 数据的预处理

从教学质量评价指标体系的二级指标中，易得到许多非数据的资料，因此必须对非数据资料进行数据化。在数据化时，还可能出现一些逆数据，须转化为正向数据。可根据数据的不同性质，采用不一样的处理方法。

图1教学质量综合评价指标体系结构图

2.1 定性指标定量化

实验数据采用问卷调查和查阅资料的方式获得。问卷中常设有(好、较好、一般、不好)几个回答方式供被调查者选择，利用被调查者选择某一回答方式的比率与权重相乘的综合得分作为该项的得分，即：

式中：xij——第j门课程第i项指标的评价得分；

vi1、vi2、vi3、vi4——答案依次为好、较好、一般、不好的比率；

w1j、w2j、w3j、w4j——答案依次为好、较好、一般、不好的权重。

2.2 逆数据正向化

将已经定量化的逆数据，用求倒数的方法化为正向指标，即：

其中，xij′为原始数据逆指标。

3 教学质量评价模型的建立

3.1 原始数据

根据教学质量评价体系中的25个二级指标，医药科学与设计专业学生对10门课程(分别用C1，C2，…，C10表示)进行评定，得到250个原始数据，见表1。

为了使主成分的内涵得到更客观的说明，对表1中的数据进行定性指标定量化处理，此外采用Z-score标准公式将原始指标数据标准化：

表1 医药科学与设计专业学生对10门课程的评定结果

运用软件SPSS16.0进行相关数据操作。利用因子解释原有变量的总方差分析结果见表2，并得因子得分系数矩阵(见表3)。用KMO检验和Bartlett′s球体检验可得KMO统计量为0.629，大于0.5，伴随矩阵P值接近0。从实验结果分析教学质量评价体系的 25个二级指标之间存在较强的相关关系，因此，教学质量评价指标适合作因子分析。

由表2可知，SPSS提取的8个特征值都大于1的公因子，其累计方差贡献率已达97.421%。一般累计方差达到80%就可以提取公因子，所以本次研究提取这8个公因子来反映25个二级指标。在未经旋转之前，由于同一个公因子在除了个别变量之外的其他变量上的载荷都相差不大，指标所反映的97.421%的信息无法解释各公因子的含义，无法进行因子命名，因此必须进行因子旋转。

在软件中，执行“Sorted by size”命令，得到由8个因子组成的因子载荷矩阵。因子1在X21、X1、X3、X19、X6共5个变量有较大载荷，可命名为“教师基本素养因子”；因子2在X22、X18、X20、X15、X8共5个变量有较大载荷，命名为“教学形式因子”；因子3在X7、X14、X13、X4共4个变量上有较大载荷，可命名为“教学内容因子”；因子4在X5、X2、X9、X17共4个变量有较大载荷，命名为“教堂教态因子”；因子5在X23、X24、X25共3个变量上有较大载荷，命名为“教学内容因子”；因子6在X11、X10共2个变量上有较大载荷，可以命名为“课堂组织安排因子”；因子7只对X12变量有较大载荷，因此命名为“教学设计因子”；因子8只对X16变量有较大载荷，因此可命名为“教学效果因子”。于是，对原有教学质量评价的25个评价指标，进行分类，总结出8个公因子。

于是得分函数(用矩阵的形式给出)为：

F=XA

其中，F表示各公因子得分向量，也可表示为F=(F1，F2，…,F8)，X表示25个评价指标向量X=(X1，X2,…,X25)，A表示公因子的得分系数矩阵。

表2 利用因子解释原有变量的总方差分析结果

以表2中前8个公因子方差贡献率为权的αi作为因子加权总分，得评价总分函数：

其中，α1=18.867，α2=16.191，α3=14.841，α4=11.933，α5=11.577，α6=9.544，α7=7.268，α8=7.182。

由表2知，前8个公因子的累计方差贡献率达97.421%，故利用前8个公因子进行教学质量评价是可行、可靠的。运用Matlab 8.0运算得到不同课程的公因子得分系数矩阵，见表4。

表3 因子得分系数矩阵

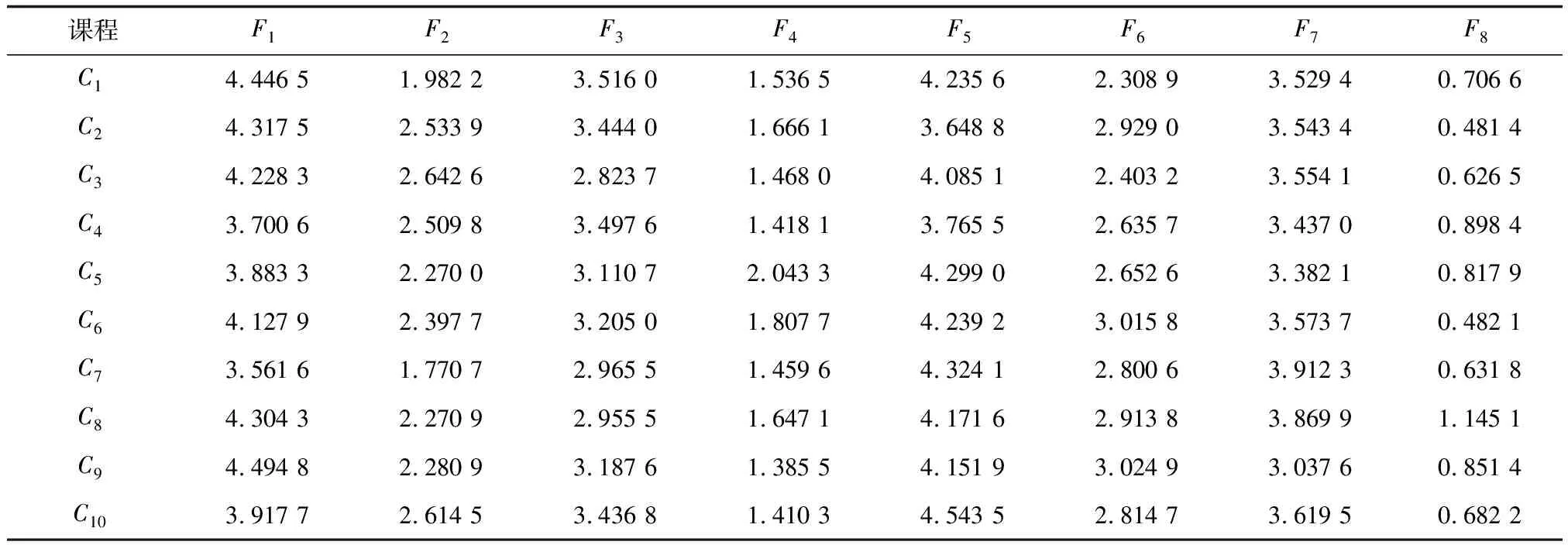
表4 不同课程的公因子得分系数矩阵

最后再根据评价总分函数，计算不同课程的评价总分，见表5。

3.4 教学质量评价模型的检验

为了检验教学质量评价模型的评价效果，通过对比传统评价法对教学质量的综合评价结果证实本次研究所建立的评价模型与传统评价法具有较好的一致性，只有课程C1和C5排序位置变换了，其余课程的结果跟传统评价法得到的教学质量综合评价结果一致(见表5、6)。

表5 基于因子分析法的教学质量评价结果

表6 传统方法对教学质量的评价结果

4 结 语

综合运用因子分析理论与数学软件，建立了教学质量评价模型，对10门课程的教学质量做出了评价，评价结果与传统评价法的评价结果基本一致，说明了本次提出的基于因子分析法的教学质量评价方法切实可行。

本次提出的教学质量评价模型不受主观因素影响，能够做到标准化评价。评价结果具有一定的客观性和可行性，能够更加真实地反映教学质量的优劣。但由于教学质量评价涉及的因素较多，而此次仅考虑了25个原始指标，因此需要进一步扩大评价指标个数和补充评价课程数量来扩大模型的适用性。