含缺陷压力管道的安全评定技术研究

洪力阳， 陈 玲， 张永发

(海军工程大学，湖北 武汉 430033)

0 前 言

压力管道是是利用一定的压力，输送气体或者液体的管状设备，能广泛应用于各种民用和工业领域，尤其在流体的输送方面，管道运输具有不可取代的突出优势。然而工业管道在服役期间存在制管和施工缺陷，可能会因为腐蚀、机械损伤等因素引起管线的泄漏和开裂，导致火灾、爆炸中毒等事故发生，因此其安全评定工作非常重要。

对于船用核动力管道，在工业管道的基础上还要考虑辐照以及海水腐蚀对于缺陷的影响；热应力循环和高温蠕变作用对于管道疲劳寿命的发展也不可忽视。本文通过总结国内外常用的压力管道安全评定技术，为下一步研究舰船核动力管道安全评定方法提供参考。

1 缺陷类别

在对含缺陷管道进行安全评定之前，首先需要了解管道的缺陷类别，认识各种缺陷的表现形式，以便更好地选用合适的安全评定方法。根据缺陷的几何特征、性质、位置以及方向等方面，我们可以将缺陷划分为不同的类别。

1.1 根据性质进行划分

根据缺陷的不同性质，我们可以将其分为裂纹、孔穴、固体夹杂、未熔合、未焊透等等，具体情况见表1。

表1 缺陷的类别、含义及其具体形式

1.2 根据位置进行划分

根据缺陷的位置可将其分为穿透缺陷、内表面缺陷、外表面缺陷和埋藏缺陷，具体情况见图1。

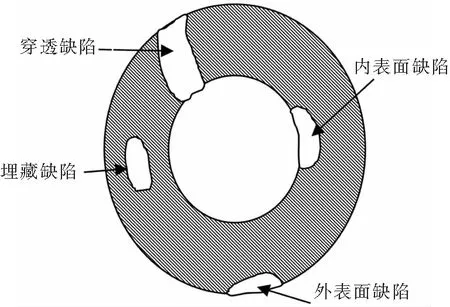
图1 缺陷类型

1.3 根据几何特征进行划分

根据缺陷的几何特征可将其分为平面型缺陷和体积型缺陷。平面型缺陷也叫裂纹型缺陷，包括裂纹、未熔合、夹层等等缺陷类型；体积型缺陷则包括孔穴、夹渣等。

在安全评定分析中，平面型缺陷和体积型缺陷是最常划分的方式，一般在进行安全评定时会将其进行相应的规则化(表征)，具体情况见图2和图3。

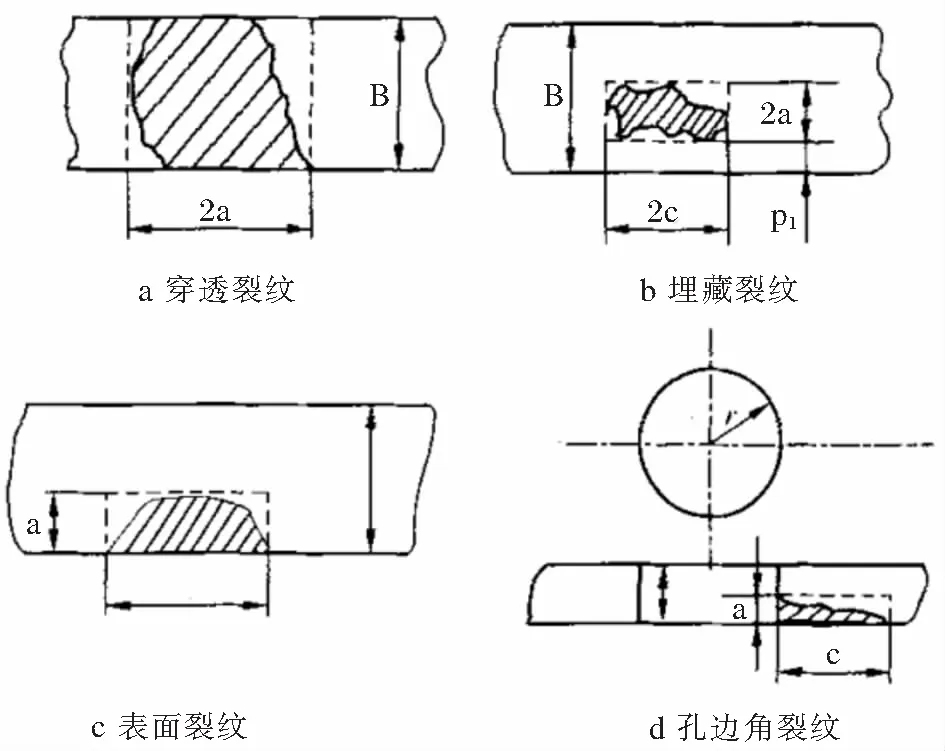
图2 平面型缺陷的表征

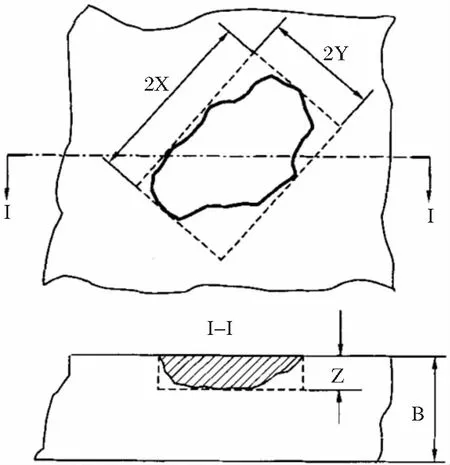
图3 体积型缺陷的表征

此外，还可以根据缺陷方向分为径向缺陷和环状缺陷，按材料和加工工艺分为焊接缺陷、铸造缺陷、锻压缺陷等。

2 评定方法介绍

国际上自20世纪70年代初期就开始对含缺陷管道的安全评定方法进行研究，主要有塑性极限载荷评价方法、弹塑性强度理论、断裂力学评价方法以及双判据评价方法等。因此可以根据不同的缺陷类别和表现形式，选用合适的安全评定方法。

2.1 塑性极限载荷评价方法

由于压力管道通常是对接焊缝，焊接缺陷一般为环向缺陷，相对于压力容器，缺陷的尺寸较小，壁厚薄，材料的韧性较好，因此失效模式通常是由极限载荷控制的塑形失效。因此可以根据净截面屈服准则和最大应力准则来进行评定[1]。

2.1.1 净截面屈服准则(NSC)

净截面屈服准则最早由Kanninen等人提出。该准则认为在弯矩或同时施加内压的作用下，含环向缺陷的压力管道所在横截面进入全面屈服时会产生失效。若考虑材料的应变硬化现象，那么管道的横截面应力达到流变应力时将处于极限状态。由此可以得到该管道能承受的最大弯矩MNRC。公式如下：

MNRC=2σfR2t(2sinβ-fsinα)

式中：σf指流变应力，一般取材料的强度极限与屈服极限的平均值，MPa；R，t分别表示管道的平均半径和壁厚，mm；α是管道所含缺陷的半周角；β是由缺陷的存在引起的管道断面的抗弯中性轴的偏离角；f是管道所含缺陷的深度a与壁厚t之比，f=a/t。

后来在大量试验基础上对其进行了修正，分别是无因子塑性参数DPZP的修正系数MPZ，管子材料的修正系数Mf以及管道的椭圆化修正因子MV。修正后实际承载能力M为：

M=(MPZMfMv)MNSC

式中MNSC是由原净截面屈服准则计算的结果。

2.1.2 最大应力准则

最大应力准则最早由德国MPA材料研究所在大量试验基础上提出。该准则认为其裂纹(环向裂纹的管道)所在截面内的最大应力达到材料的强度极限σu时产生失效，此时最大弯矩M为：

2.2 线弹性断裂力学评定方法

1948年Irwin发表了论文《Fracture Dynamics》，标志着断裂力学成为一门独立的工程学科，随后大量的研究集中于线弹性断裂力学。

该理论认为裂纹体各部分的应力和应变在脆性断裂过程中处于线弹性状态，塑性变形阶段只存在于裂纹尖端的极小区域内。处理方式有两种：一种是通过研究裂纹尖端附近的应力应变场，运用应力强度因子及对应的断裂韧度K判据而提出的应力应变分析方法；另一种是能量分析方法，主要是研究裂纹扩展时系统能量的变化，运用能量释放率及其对应的断裂韧度和G判据[2]。

线弹性断裂力学将结构视为不发生屈服的弹性体，因此一般适用于脆性材料的裂纹型缺陷判定。

2.2.1 应力应变分析法(K判据)

该方法假设有一块无限大板(承受均匀拉应力)，含有一处长为2a的I型穿透裂纹，如图4所示。

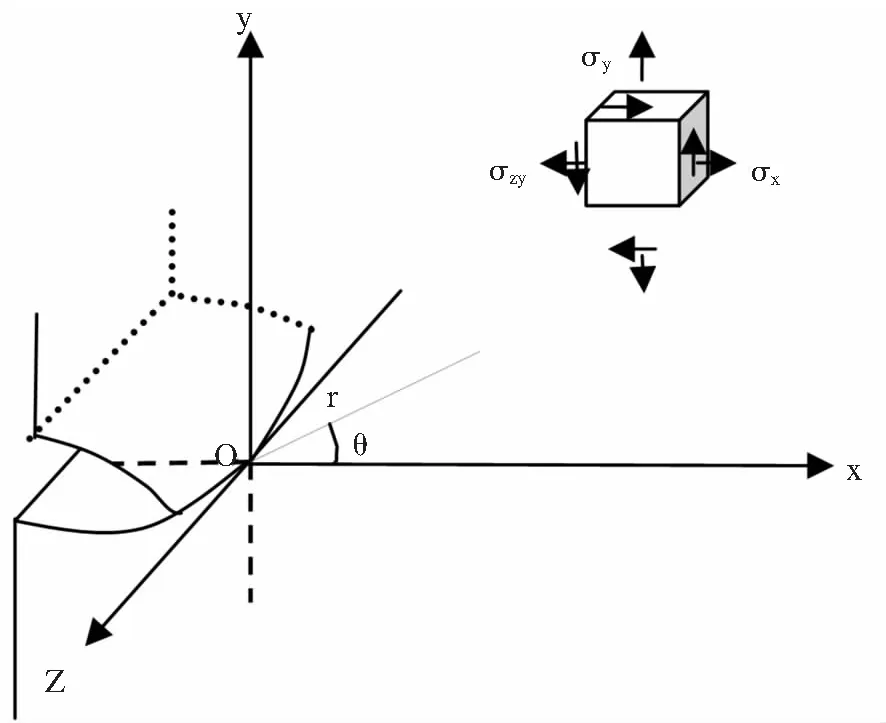
图4 裂纹尖端的应力分析

若给定裂纹尖端附近一点(r，θ)，且裂纹体的材料一定，则该点的位移分量、各应力和应变由KI值唯一确定，KI值越大对应的值也越高。因此KI可反映裂纹尖端区域应力场的强度，故称之为应力强度因子，它综合反映了裂纹位置、长度以及外加应力对裂纹尖端应力场强度的影响，其表达式一般为：

式中：Y是裂纹形状系数，取决于裂纹的类型；σ是应力，MPa；a是裂纹尺寸。

在裂纹尖端足够大的范围内，若其应力值达到了材料的断裂强度(即裂纹尺寸a或应力σ达到临界值)，那么裂纹就会因为失稳扩展而导致断裂，这时KI也达到一个临界值，记为KIC，单位为MPa·m1/2。

因此，可以根据KI与KIC值的相对大小建立裂纹失稳扩展脆断的断裂K判据：

KI≥KIC

受力时，裂纹体只要满足上述条件，就会发生脆性断裂；反之，即使存在裂纹，也不会发生断裂。

2.2.2 能量分析法(G判据)

Griffith最早用能量法研究脆性材料的断裂强度及其受裂纹的影响，提出驱使裂纹扩展的动力是弹性能的释放率，令其为GI：

GI为裂纹扩展的能量释放率，J/mm2。当GI增大到某一临界值GIC，裂纹便失稳扩展而断裂，GIC称为断裂韧度。

因此，可以根据GI和GIC的相对大小建立裂纹失稳扩展的力学条件，即G判据：GI≥GIC

2.3 弹塑性断裂力学评定方法

弹塑性断裂评定的方法主要建立在弹塑性断裂力学的基础上，主要可以分为COD法(裂纹尖端张开位移法)和J积分理论法[2]。一般用于裂纹型缺陷的评定过程中。

2.3.1 裂纹尖端张开位移法(COD法)

1965年，WELLS提出了弹塑性断裂力学的COD理论，后发展为半经验的COD设计曲线方法，成为20世纪70年代国际缺陷评定规范主要采用的评定方法。

裂纹体受载后，在裂纹尖端沿垂直裂纹方向所产生的位移即为裂纹尖端张开位移，可用δ表示。在小范围屈服条件下，裂纹尖端的塑性区进行修正，裂纹由a虚拟扩展到a+ry，尖端由O点移到O’，如图5所示。

图5 裂纹尖端张开位移

δ的临界值称为断裂韧度，表示材料阻止裂纹开始扩展的能力，根据δ和δC的相对大小关系，可以建立断裂δ判据：

δ≥δC

而对于大范围的屈服，KI与GI都已不再适用，但COD仍可以进行评估。Dugdale应用Muskhelishvili复变函数解弹性问题的方法，提出带状屈服模型(DM模型)，导出了塑性条件下的COD表达式，如图6所示。

图6 带状屈服模型

设有一长2a的I型穿透裂纹存在于塑性材料无限大薄板中，远处平均作用应力为σ，裂纹尖端的塑性区ρ呈尖劈型。若沿x轴将塑性区割开，则裂纹长度由原来的2a变为2c，在割面上下方代之以应力σS，以阻止裂纹张开，于是该模型就变为在(a，c)和(-a，c)区间作用有σS，无限远处有均匀应力σ的线弹性问题。则：

2.3.2 J积分评定法

1968年，Rice提出了J积分，Hutchinson证明了J积分可以用来描述弹塑性体中裂纹的扩展，在这之后，逐步发展为弹塑性断裂力学。J积分理论可定量的描述裂纹体的应力应变场的强度，如图7所示，设有一单位长度的I型裂纹体，取一逆时针回路Γ，其应变能密度为ω(包围体积内的)，Γ上任意一点的作用力为T。

图7 J积分的定义

若s为Γ周界弧长，u为该点位移矢量，则定义J积分为：

JI为I型裂纹的能量线积分，在平面应变的条件下，当应力应变场的能量达到使裂纹开始扩展的临界状态时(即外力达到破坏载荷时)，JI达到相应的临界值JIC，也可称为断裂韧度。

根据JI与JIC的相互关系，可以建立J判据，即：

JI≥JIC

若满足上式，裂纹就会开裂。

2.4 英国R6评定方法

1976年，英国中央电力局(CEGB)发表了“带缺陷结构的完整性评定”(R/H/R6)报告，制定了第一条失效评定曲线，因此R6法也称为失效评定曲线法[3]，一般用于平面型缺陷评定。

直至1986年，R6法经过了3次修订，习惯上将之前的失效评定曲线法称为“老R6法”，它以D-M模型为依据。后来经美国EPRI研究，使用J积分取代窄条区屈服模型。该方法分别取纵坐标和横坐标为Kr、Lr：

Kr=KI/KIC，Lr=P/P0

Kr反映了结构脆性断裂的程度，Lr是施加载荷P与塑性失稳极限载荷P0的比值，反映了结构塑性失稳程度。因此R6法也被称为双判据评定法，当评定点(Lr，Kr)落在评定曲线外时，表示结构失效；反之，则说明结构是安全的。

习惯上将CEGB于1986年修改的R6标准称为新R6标准，该标准以J积分为基础，考虑了材料的应变硬化效应，建立3种可选择的失效评定曲线，在EPRI的基础上做了简化。另外改进了裂纹的延性稳定扩展处理方法，提出3种类型的缺陷评定方法，可根据具体的情况选用。

新R6失效评定曲线的一般形式如图8所示，可用一条截断线和一条连续的曲线表示。

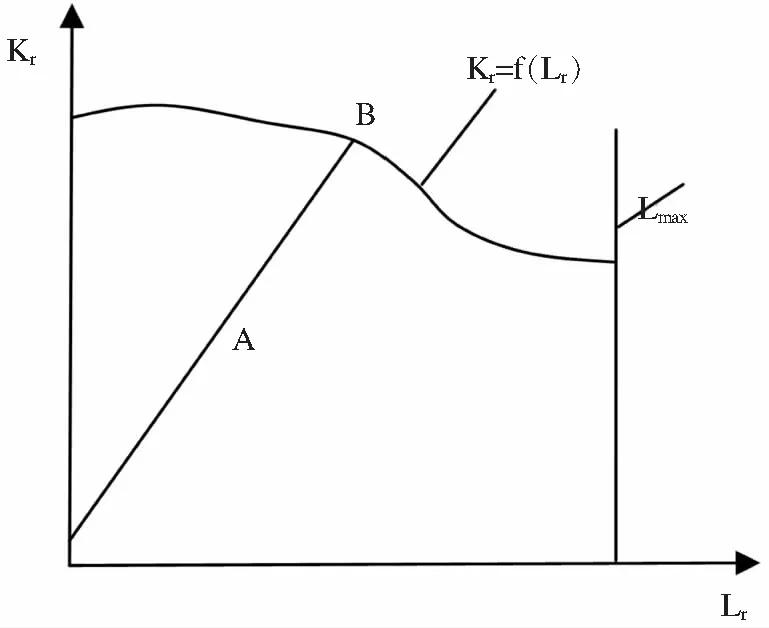
图8 新R6失效评定曲线的一般形式

截断线Lmax表示结构塑性失稳载荷与屈服载荷在缺陷尺寸很小时的比值，若Lr>Lmax，则Kr=f(Lr)=0。

R6法是美国ASME规范IWB-3640和IWB-3650管道评定方法的基础，取用K判据断裂应力强度因子理论、COD理论以及J积分理论等众家之长和最新研究成果，能够判别含缺陷结构的潜在失效模式，进行结构的脆性断裂、弹塑性断裂和塑性失稳分析，因此广泛用于管道的安全评定中。之后R6标准又增设附录9，即核压力管道LBB评定方法，也可将其用于评定高温蠕变场合，提出与时间有关的LBB失效评定图Kr=f(Lr，T)。

2.5 英国BS7910法

1999年，英国制定《焊接结构缺陷验收评定方法指南》(BS7910)评定标准。该标准共有3个评定级别，分别为一级简单评定、二级常规评定以及三级延性撕裂评定[4]，主要用于平面型缺陷的评定。其中的一级安全评定最为保守，主要应用在相关评定数据较少的情况；二级评定为常规评定方法；三级评定为最高级别评定方法，主要是应对需要分析裂纹的稳定撕裂断裂或者高应变硬化指数的材料。

本文主要对BS7910-2005评价标准中的一级安全评定方法进行介绍。一级安全评定包括两种(1A法与1B法)。

2.5.1 1A级评定

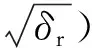
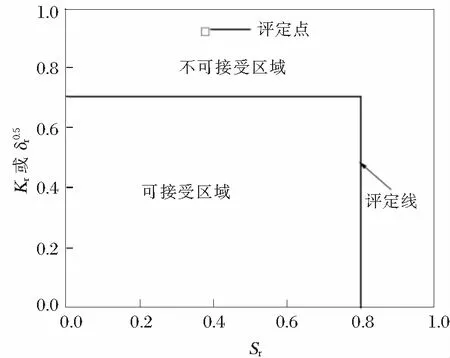
图9 1A级失效评定

其中：Sr=σref/σf，Kr=KI/Kmat

式中：σref为参考应力；σf为流变应力，等于抗拉强度σb与屈服强度σs的算术平均值，最大值为1.2σs；KI为应力强度因子；Kmat为试验实测的断裂韧性值，Kmat可通过夏比冲击试验测得。

两条评定线分别是Sr等于0.8的垂直线和Kr等于0.707的水平直线，若评定点在矩形区域之内则安全，反之则不安全。

2.5.2 1B级评定方法

2.6 欧洲SINTAP评定法

1999年，欧洲委员会制定了欧洲工业结构完整性评定方法，该方法根据管道材料的脆断、塑性破坏以及二者之间的相互作用，使用失效评定图(FAD)和裂纹推动作为分析方法，对焊接结构进行合于使用的评定。根据材料数据的详尽程度可分为3个标准等级和3个先进等级[5]。

SINTAP主要通过提高数据质量来降低保守性，是建立在输入数据质量基础上的分级结构：最复杂、最准确的等级需要相应高质量的输入数据。

SINTAP使用的是FAD法，与R6法和BS7910相同，可用于平面型缺陷评定，但在参数计算、应力分析等方面有所区别：

1)基本方程

第1级评定与材料的Lüders平台相关，对于有Lüders屈服平台的材料，其评定曲线函数：

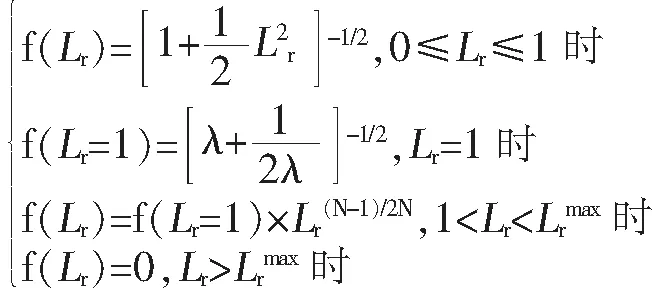
对于连续屈服材料，曲线函数：

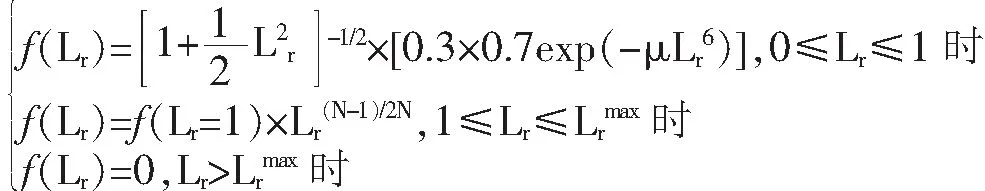
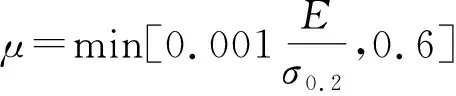
2)SINTAP可以在缺少详细的应力应变数据时通过对大量钢材性能的研究，来提供材料应变硬化性能、屈强比以及屈服平台的估算方法。

3)提出由AKV(冲击功)估算铁素体钢解理断裂区断裂韧度下限值的方法。由于AKV与启裂断裂韧度间无明确的简单数学关系，且此下限值在工程评定中一般无法测得，因此此估算虽然数据很保守(甚至只有实际值的五分之一)，但仍然很有意义。

4)在处理时不仅采用R6的ρ因子法，同时也提出新的V因子来表示二次应力的影响。若V>1，那么表示二次应力超过了弹性的估计值，则塑性情况下J积分值发生变化；反之，若V<1，则表示二次应力松弛；若V=0，则二次应力可忽略不计。

5)阐述了一种计算约束等级的方法，以超静态Q-应力或裂纹尖端的弹性T-应力为形式，修改CDF或FAD法来考虑效果。

6)给出了可靠性评定法以及软件PRO-SINTAP，采用Monte Carlo数学模拟以及近似的一阶可靠性过程。在评定过程中将断裂韧度看为随机变量来处理断裂韧度的分散性问题，目前已经有基于SINTAP断裂韧度概率密度的分布模型，采用柯尔莫戈洛夫检验法和A2-W2检验法来研究管线的热影响区断裂韧度CTOD的方法。

2.7 美国ASME系列规范评定方法

美国的ASME(机械工程师协会)是国际上安全分析与评价领域最早和最权威的机构。1963年颁布了第一版ASME SECTION III《核设施元件制造规则》，1984年发布了适用于剩余强度评价的ASME B31G-1984，也是国际上应用最广泛的评价标准之一[6]，主要用于体积型缺陷的评定。

本文主要介绍ASME第XI卷《核电厂部件在役检查规则》中的IWB-3650评价法及附录H《铁素体钢管道缺陷评定规程及验收准则》的有关内容。

IWB-3650法可对脆性断裂失效、塑性失稳失效以及弹塑性断裂(包括启裂后韧性撕裂材料抗力增强至失稳的极限载荷分析)进行评定。可以根据管径以及缺陷的几何尺寸、材料性能和外载大小的计算参量(SC)值判别出潜在的失效模式，然后查出相应的表格和算式。其中表格和算式已经通过大量的理论分析和数值计算整理得到，因此方法非常简便。具体的失效模式判别准则和FAD图如图10和11所示。LEFM是线弹性断裂力学，EPFM是弹塑性断裂力学。

图10 失效模式判别准则

图11 失效评定

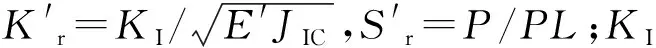
实际评定中由于JIC难以测定，因此可采用ASME推荐保守值，如评定环向缺陷(碳钢材料)时σy=27.1Ksi(即186.9 MPa)，JIC=600 Ib/in(0.105 MN/m)。

2.8 国内的评定方法

目前国内使用的主要标准有如下4项：API579-1-20 07、BS7910-2013、GB/T19624-2004《在用含缺陷压力容器安全评价》[7]以及SY/T6477-2014《含缺陷油气输送管道剩余强度评价方法》[8]。

GB/T19624-2004标准依据合乎使用和“最弱环”原则，将缺陷分为平面缺陷和体积缺陷，建立了应用简便、精度高，且可适用于任意应力应变关系材料的含周向面型缺陷压力管道的U因子工程评定方法[7]。具体评价流程见图12和13。

SY/T6477-2014针对管道工程中常见的体积型缺陷、含裂纹型缺陷、弥散型缺陷，以对管道的定量检测为基础，确定其最大许用工作压力MAWP以及当前工况下的最大允许缺陷尺寸。再根据缺陷的动力学发展规律和材料性能退化规律，运用软件计算其剩余强度和寿命[8]。以体积型缺陷为例，目前国内已经在此有了软件开发和应用，具体评价流程如图14。

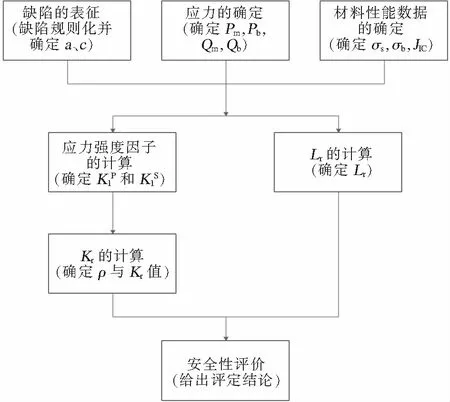
图12 平面型缺陷的评定流程

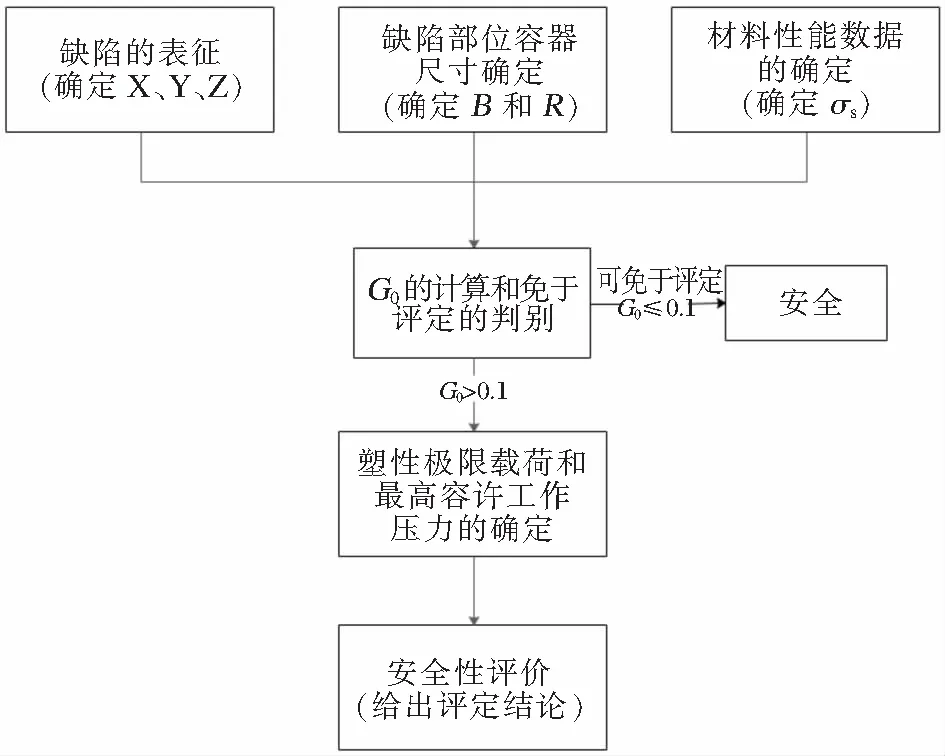
图13 体积型缺陷的评定流程

以上所有标准都采用双判据失效评估图方法，兼顾了脆性断裂失效和塑性失稳失效，是断裂力学评价方法和塑性极限载荷评价方法的结合。

3 核动力管道的评价标准及其流程

在核电方面，目前国内核电机组的役前和在役检查主要按照ASME颁布的《锅炉及压力容器规范》第XI卷《核电厂部件在役检查规则》或法国的《压水堆核岛机械设备在役检查规则》(RSE-M规范)的要求执行[9]。

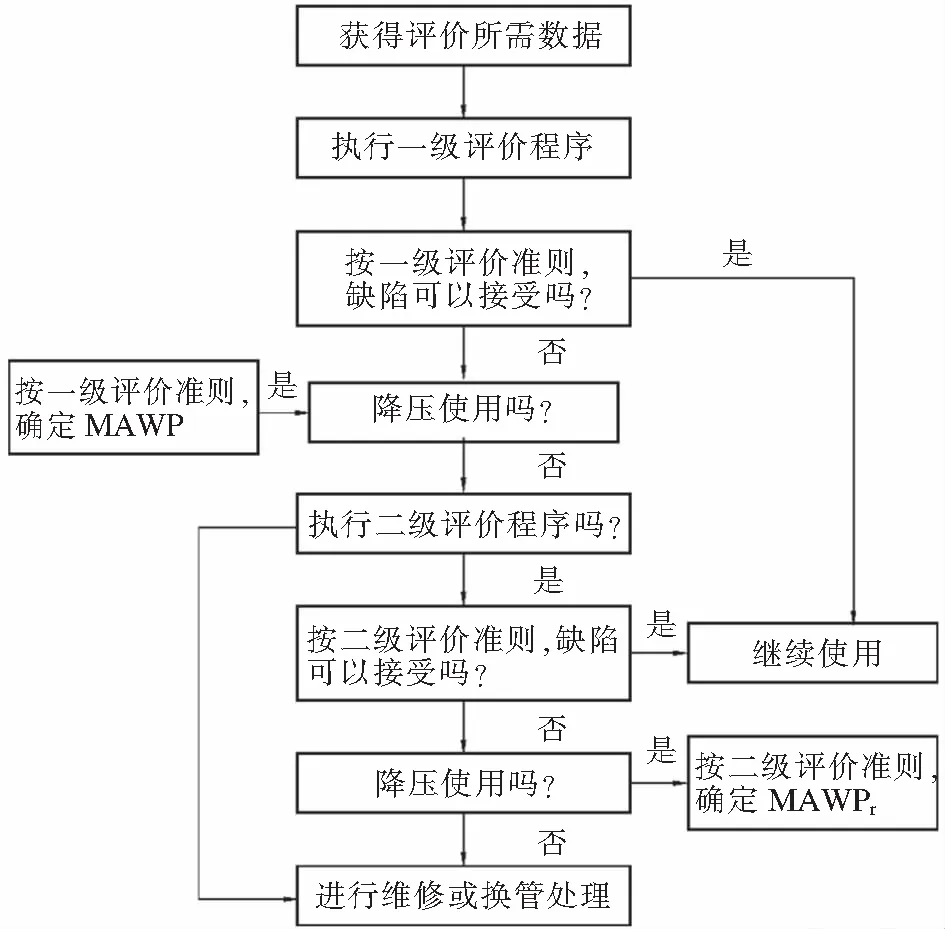
图14 含体积型缺陷管道的剩余强度的评价流程

在核电厂核级焊缝的役前和在役检查过程中需要对缺陷进行处理，以判断其是否满足规范的要求以及应该采取何种手段处理缺陷，具体流程如图15所示。

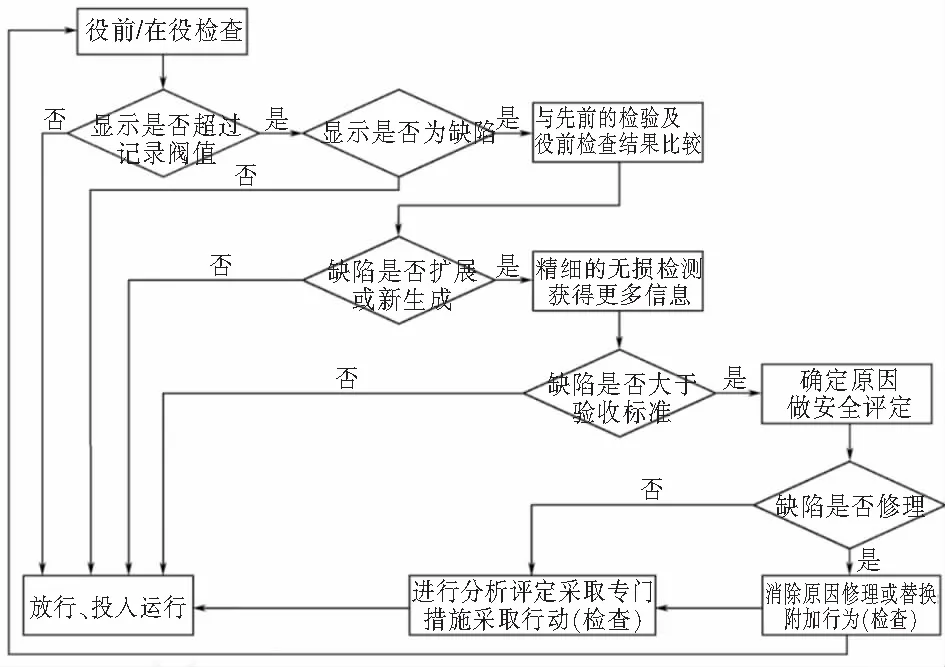
图15 缺陷处理流程

在评价过程中，若要求的判据都满足，则该含缺陷管道适用于目前的工作条件，只要采取适当措施就可以在当前工作条件下继续安全运行。若评价结果表明该含缺陷管道不适合当前操作条件，则宜进行降级使用，计算其MAWP值(最大允许工作压力)，再进行进一步的分析。

在船用核动力方面，目前国内主要是通过检修过程中的无损探伤来进行判定，还没有形成较为规范的评价方法，辐照作用以及热应力对于含缺陷管道的剩余强度和疲劳寿命的影响也没有进一步的研究。

4 研究方向和进度

对于下一步研究含缺陷核动力管道的安全评定方法，可以借鉴ASME IWB-3650以及双判据评定方法，结合无损探伤的缺陷数据、辐照和热应力疲劳的影响，采用ANSYS建模分析和建立FAD失效图的方法来进行评定，具体的评价流程还有待进一步的分析论证。

目前前期的各项调研工作已经基本完成，对于管道的材料性能参数、无损探伤法以及ANSYS分析软件的使用等都有了基本的认识。存在的问题是关于含缺陷管道的数据建模、应力值分析以及边界条件的限定还有待进一步的研究论证，计算结果、可靠性以及寿命预测也需要通过实际的检修工作跟踪论证。

5 结 论

本文针对含缺陷压力管道的评定方法以及各参照标准，对目前国内外的管道安全评定进行了较为系统和全面的介绍。对于核用管道，国际上主要是参照ASME协会的IWB-3650法和法国的RSE-M规范的要求来进行评定。我国目前也是借鉴了此类标准和规范，结合工程的实际需求，制定了适用性的评定方法。但是目前在船用核动力领域还没有针对性的评定方法，核管道的各项数据也还不完善，不能适应目前工程以及实际任务中的需求。本文指为下一步研究舰船核动力领域的含缺陷压力管道安全评定方法提供参考和研究基础。