基于时空模式的仓库物流配送路径优化

徐少堃

(安徽审计职业学院 商学系，安徽 合肥230001)

仓库物流配送路径优化的(Optimization of warehouse logistics distribution path，OWLDP)主要目的是找到从初始点出发并只经过一次给定点再返回初始点的最小成本路径[1]。这也是最短路径算法的实际应用，也是当前地理信息系统基础软件的重要功能[2]。回避方法[3]在部分寻优方面是具有较好的性能，然而这种方法对初始参数设置以及邻接区结构具有很强的依赖性；蚁群算法[4]对于初始路径选择并没有太大的依赖性，然而由于在初期缺乏相关信息，算法的收敛效率会受到影响[5]。

由上述分析可知，现有的方法具有较大的计算开销，而且对于算法依赖于参数的选择，对初始值具有较大的依赖性。当前关于OWLDP的研究主要为混合启发式算法，即利用多种改善算法以及邻接区查找结构来进行算法设计，以提高算法的整体效率，同时扩展了算法的适用范围。混合启发式算法还能够增强OWLDP的准确率与效率，这也是当前OWLDP问题的重点研究方向。本文充分发挥了时空模式在整体寻优方面的强大能力，以及其在回避查找方面的独有功能，进行OWLDP问题的求解，以增强OWLDP求解方案的寻优能力、运行效率、结果准时性。

1 仓库物流配送路径优化方法

1.1 仓库物流配送方法选择

回避查找是一种模拟人脑短期记忆功能的整体逐步寻优方法，它使用回避准则来避免进行无意义的循环计算，而且可基于藐视准则接受差解，确保在不同范围内都能实现对有效路径的探测，具有较强的部分查找能力。时空模式(Spatio-temporal pattern, SP)多用于对大规模、多目标问题的整体改善问题，能够从解的范围内的多个点、角度出发，实现一种自我学习式的搜索，具有十分突出的整体寻优能力。采取标准回避方法(Standard avoidance method，SAM)时，通过单纯的优化操作建造的邻接区。由于所得到的解具有较高相似性，故此方法容易陷入局部最优。同时，在采用时空模式时，变异计算单元会导致具有新特征个体的产生，由此增强了路径组合的多样性。

本文所提出的OWLDP首先使用时空模式作为弥漫方案建造邻接区，由此使得群体个体广泛地分布在解的大部分范围内。通过这种方式能够确保方法具有较好的寻优能力。随后的聚合方案使用回避查找方法，该方法能够突破以往的局部最优解，有效地避免过早的收敛。在弥漫决策中充分反映了群体智慧，极大地增加解的多样性，而且利用聚合政策能够促进整体执行力的提高，增加全局最优解的可能性。此外，随着迭代次数的不断增加，通过弥漫决策能够形成对聚合决策的有效约束。通过这种相互作用，能够有效的增强内部的竞争机制，从而得到最优解。

OWLDP的主要核心元素如下。

适应度函数：利用该函数能够有效地分析回路的质量水平，一般而言，对于个体适应度的评价是通过路径长度实现的。如公式(1)所示为计算第x条路径长度的公式，dis(g)代表了相邻两点间之间的距离，Cn(i)代表了第i个点

(1)

当初始回路途径点的位置发生改变时，会得到新的回路集合，将其称之为邻接区。利用SP方法的变异计算单元能够增加解范围的多样性。为了能够对邻接区结构进行改善，扩展部分查找的范围，本文采用多种方法构造初始回路的邻接区，包括对变异计算单元进行逆序、交换、移位等。一次优化指的是当初始回路运动到其邻接区中的最优回路，而下一次迭代的初始回路就是本次所最终采纳的优化。通过对计算单元的选择能够向着最有可能的查找范围进行探测，本文利用了精英选择法，以提高回避查找的速度，即在邻接区中确定最优的10个回路，将其作为候选解集，来进行回避查找。

1.2 物流配送路径优化过程

图1为本文OWLDP方法的详细实现过程。

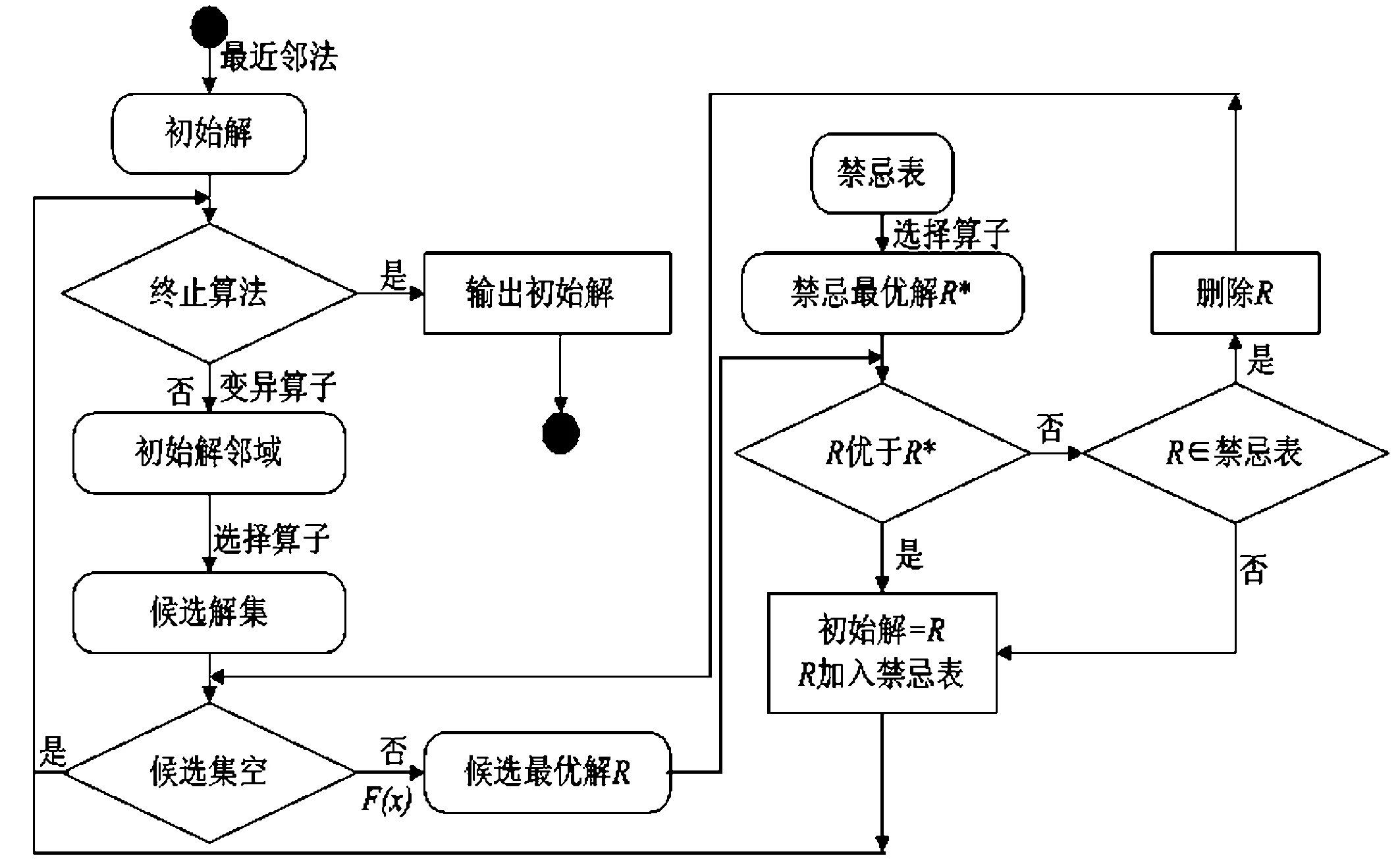
图1 OWLDP时空模式具体过程

由于最优回避对象可能在查找过程中被删除，故此，候选解集是不会处于完全回避之中的。如果候选解集属于空集，则会在上一次初始解附近范围内进行查找，本文方法具有O(n2)的时间复杂度。

1.3 物流配送路径优化建模

物流公司将商品送到合肥市二环内的客户地点。所有这些交付都是从配送中心开始的。运输问题是如何将不同的顾客分成不同的运输路线，这样就减少了运输车的数量，减少了总行程。此外，客户配对或路径选择应遵守以下限制：

● 运输车的容量为136个单位的商品；

● 司机每天工作时间不超过11小时；

● 每辆卡车在3个以上的位置不停车；

● 一些客户必须是路线上的第一站；

● 有些客户不能与其他客户配对，因此需要一辆运输车单独为他们服务；

● 所有客户的实际交货期必须在客户确定的最早和最新的交货期之间。

本文将仓库物流配送路径优化问题建模成混合整数规划，如下所示：

(2)

(3)

(4)

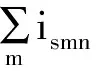
(5)

(6)

(7)

(8)

式(2)是路径优化问题的目标函数，目标是最小化的物流配送总成本。plm是指从点l到点m的运输成本。当运输车n使用经过节点l和节点m时，ilmn=1；否则ilmn=0。变量tlm是运输车从节点l到节点m的时间。um是运输车在节点m卸货的时间。约束条件(3)确保了每次只有一辆运输车进入或者离开中间节点。约束条件(4)是流守恒条件。约束条件(5)限制了每辆运输车仅能被使用一次。约束(6)限制了每辆运输车最大停经的站点数量，max_s是最大的停经站点数。约束(7)保证了每辆车的商品不超过车的最大容量，max_c是运输车的最大容量。约束(8)限制了运输车司机的工作时间，其中，max_T是最大的工作时间。

2 试验与讨论

2.1 试验环境

本文在SuperMap二次开发平台上验证了OWLDP时空模式，而且结合合肥市二环内的路径测试了本文所提出的方法，在路径中共有2764个路段，结点共有1769个。在本次实验中，从配送路径中通过随机抽取的方式确定了三组结点，确定的数据规模分别为5、10、20，并将计算结果与回避查找、时空模式和MapInfo软件的结果进行对比。测试环境如表1所示。

表1 测试环境

2.2 实验结果

根据现有方法的参数设置经验，各参数取值如表2所示，N为结点个数。

表2 方法的参数设置

基于SAM的方法具有较低的平均及时性，因此本文实验将该方法具有的计算及时性作为基准，对本文方法的收敛效果进行分析。图2是方法具有的及时性以及其耗费时间之间的关系。分析实验结果能够得出，如果能够将及时性增长率保持在[-10%，0]范围中，与SP相比，OWLDP将会具有更高的平均收敛速度；当设定的及时性不断提高时，OWLDP在效率方面的优势是不断突出的，而如果得到的解的质量要好于参考值，则每将及时性提高1%，需要耗费的时间将会呈现出指数级增长的趋势，然而，即便如此，OWLDP仍旧具有十分突出的运行效率优势。

图2 OWLDP方法及时性——耗时曲线

如果将及时性误差保持在1%以内，则与SAM和SP方法相比，OWLDP方法不管在运行效率，还是在准时性等方面都是具有更好的性能的，而且与MapInfo的水平是一致的。如图3表示了OWLDP方法对数据进行计算的最终结果。

故此，考虑将本文提出的时空模式实施优化处理，进而实现对物流配送路径的高效利用，以推动方法运行效率的有效提高。相较于传统方法，本文的主要优点在于，具有较好的实时性，而且具有较高的准确性。

图3 约束方法针对不同结点数求解OWLDP的结果

3 结论

本文设计了一种求解仓库物流配送路径优化问题的时空模式。方法采用时空模式增强优化路径的效率。相较于简单的单纯的回避查找和SP方法而言，如果具有相同的求解及时性，那么通过本文方法能够得到更好的运行效率，具有更强的鲁棒性，更好的准时性。假定将解的及时性损失设定在1%以内在，则通过本文方法能够得到与MapInfo方法相当的运行效率。而且，由于时空模式是具有并行特性的，因此在本文方法中也是可以实现物流配送路径的并行化。