基于自相关关系网络遥感影像的动态定位方法
成艳真
(济源职业技术学院 艺术设计系,河南 济源 459000)
遥感影像普遍存在混合像元的现象[1]。软分类技术,如混合像元分解技术,能够获取像元中每一个地物类别对应的丰度,获得与类别个数相等的丰度影像,有效地解决像元混合问题[2-3]。然而混合像元分解仅能获取各端元组分的丰度,无法确定各种地物在像元空间中的具体位置,仍然会造成遥感影像空间细节信息的丢失[4-5]。为了有效的解决这一不足,当前国内外对于网络遥感影像动态定位进行了深入的研究[6],提出了多种动态定位方法,包括在拓扑结构基础上确认的定位方法,即充分利用其中的非线性拟合特征提高动态定位方法的准确性。然而,以往在隐藏层拓扑结构基础上进行的网络遥感影像动态定位方法,在定位确定时更多考虑的是网络遥感影像其在像素空间内的关系,而对于其在运动级空间的关系没有进行充分考虑,这就违背了动态定位假设。因此,为了增强动态定位方法的准确性,本文提出在相关关系网络遥感影像的动态定位方法,经过仿真验证,能够极大提高定位准确性。
1 自相关关系网络遥感影像的动态定位方法
1.1 动态定位基础理论
在进行网络遥感影像动态定位前需要满足基本前提条件,也就是能够实现网络遥感影像分解,一般是通过分解高光谱影像实现,以达到网络遥感影像不同类别在像元中占据的比例大小形成更加清楚的认识,在此基础上,结合网络遥感影像动态定位的基本理论对于不同端元组分所处的空间分布状况进行分析。
根据动态定位相关理论可知,考虑到距离远近的不同,相较于较远距离的网络遥感影像动态定位方法,较近距离的更加倾向于为同一类型,而且三维遥感采用动态理论在很多实践经验中得到了有效验证。图1(a)中,已知遥感影像3×3个低分辨率像元的组分比例,从而计算出每一个像元里面不同类别的亚像元个数。其中的网络遥感影像类别有两种,以黑白两色表示,以五倍比例放大。图1(b)、(c)对于两种存在差别的空间分布状态进行了描述,从理论角度分析,图1(c)具有更大的动态定位,因而,该图更加可能为网络遥感影像动态定位分布图。
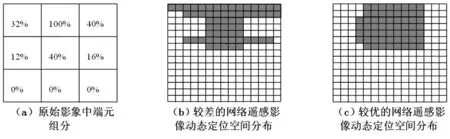
图1 网络遥感影像动态定位空间分布示意图
1.2 网络遥感影像动态定位
自相关关系网络遥感影像动态定位方法指的是利用误差反向传播实现网络遥感影像的前馈,该方法中包含了输出、输入层节点的选取,并且其中还有隐藏层。信号输入之后首先以向前传播的方式传送到隐藏层,随后在函数的作用下,将信息从隐藏层节点向着输出节点进行传输,以实现最终网络遥感影像数据的采集。本文中对于网络遥感影像动态定位方法的研究是将自相关关系算法引入到网络遥感影像上实现的,此法主要包括训练与模拟两个模块,两者使用的网络模型是一样的。
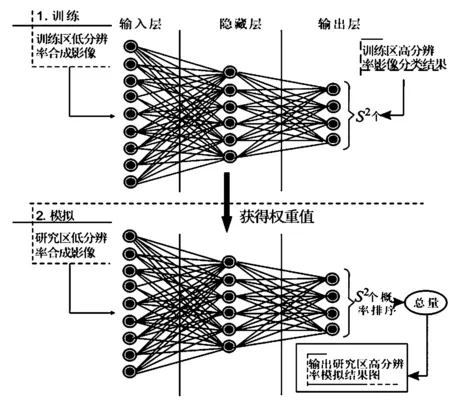
图2隐藏层拓扑结构进行动态定位方法过程示意图
图2为隐藏层拓扑结构进行动态定位示意图。在空间尺度为2的前提下,模型中输入层是在目标像元分辨率较低的情况下,网络遥感影像的丰度值,以及其在邻域内的丰度值;而输出层则为目标像元处于地分辨率时,其在高分辨率下进行影像重建时的S×S个像元,通过输出层相关节点值能够对该像元是否与该类网络遥感影像匹配进行概率方面的判断。而且,应该对像元按照其网络遥感影像动态定位概率值的大小进行排序,以达到目标类型的准确锁定,一直到能够满足该类总数,最终确定网络遥感影像动态定位空间分布状态。
网络遥感影像动态定位方法对于提高网络遥感影像准确性有较大帮助,但该方式下构建的模型其最终的定位结果和其在训练阶段进行的数据选择具有较大关联,如果数据选择的准确度较低,那么得到的结果会或多或少存在精度、细化方面的不足。而且,全局代价函数的极值点并不是单一的,这就导致更加容易出现“锯齿”问题,致使定位结果难以满足动态定位基本假设,从而较难从网络角度有效解决这些误差。
2 网络遥感影像动态定位过程
对于具有相同属性值,而所处空间位置不同的关联程度判断,可以利用自相关关系函数实现。为提高网络遥感影像的动态定位方法精度,利用自相关关系函数对网络遥感影像定位后的结果进行调整。结合自相关关系能够推出计算方式:
(1)
(2)
Wi°表示空间权重矩阵中第i行之和;W°j则为矩阵第j列之和。Nairo统计量的取值为-1至1,如果I>0则说明是正相关的,反之在I<0则为负相关,并且该值越大则说明具有越大的空间分布相关性,也就是说明存在空间聚集分布,如图3(a)所示;相反的该值越小则可说明具有较小的动态定位,如图3(b)所示;如果该值接近为零时,说明空间分布更加倾向于随机分布的状态。我们通过ENVI利用其中的随机功能得到了图3(c),计算得出此时自相关关系函数值是接近0的,因此,我们可以利用自相关关系函数Nairo统计量来对于同一属性值在所处空间位置不同时,其分布的关联相互关系。

(a)Nairo=0.5238 (b)Nairo=-0.1429 (c)Nairo=-0.0095
图3自相关关系结果示意图
3 实验与结果分析
3.1 试验影像
本文所使用的数据是武汉1999年9月的TM影像,影像具有30 m的分辨率,图4(a)所示。其中可以将其中的网络遥感影像进行大致分类:长江、居民地、湖泊、植被,考虑到长江和湖泊具有较大的水质差异,因此将其视为单独一类。类似于处理模拟数据,首先对图4(b)采取降釆样处理,从而得到分类别网络遥感影像的端元丰度影像。原始影像具有的像素是200×200像素,降采样之后得到的端元丰度影像具有50×50的像素。再利用自相关关系函数基础的隐藏层拓扑结构模型对低分辨率影像进行动态定位方法试验,得到定位结果分别如图4(c)、(d)所示。

(a)原始假彩色合成影像 (b)分类参考影像 (c)原始隐藏层拓扑结构定位结果 (d)本文方法定位结果
图4影像定位结果
3.2 试验结果比较
目视角度分析,如果是利用原始的隐藏层拓扑结构模型得到的定位结果表现为较为明显的锯齿效应,通过从目视上看,原始隐藏层拓扑结构网络模型的定位结果存在一定的锯齿效应,基于自相关关系函数得到的结果会更加的平滑,相较之下,与实际网络遥感影像分布更加切合。本文利用PCC'、kappa'系数以及混淆矩阵等方法对定位结果进行定量分析,并且引入了分析指标PCC'与kappa'以对该方法的性能进行评价。

表1 试验影像精度统计表
试验结果如表1所示。对于试验1,从表1中的精度结果比较可以看出:基于自相关关系函数的拓扑结构模型方法与原始隐藏层拓扑结构方法相比较,PCC'值和Kappa'系数分别提高了1.587%和2.4900。为了更准确地比较这两种方法在混合像元中的定位精度,分别计算其PCC'值和Kappa'系数,从表1可以看出本文方法分别将PCC'和Kappa'精度提高了5.385%和8.38%。
为了详细突出具体差异,在表2中采取了两种方法来评价试验1的混淆矩阵结果。分析表2可以看出,在自相关关系函数基础上的拓扑结构方法在定位精确度方面得到了很大提高,尤其是对于植被、湖泊、居民地这些交界区域,由于该位置的网络遥感影像类别是十分复杂的,而如果是采用传统的拓扑结构模型,对于网络遥感影像动态定位间的关联性没有进行足够的考虑,而致使得到的精确度是较低的。对比分析可得,利用本文的方法能够有效的对网络遥感影像动态定位关联信息进行考虑,具有较高的精确度,在定位精度方面具有更大的优势。

表2 试验影像1定位结果混淆矩阵对比(PCC')
4 结论
在网络遥感影像动态定位方法中,如果使用传统的隐藏层拓扑机构,对于网络遥感影像动态定位间的关系没有有效的兼顾,这就导致结果是不能满足动态定位理论的。本文通过自相关关系函数,在此基础上结合网络遥感影像实施动态定位方法,从理论层面是满足动态定位理论的。经过对比试验分析能够证明,该方法相较于传统方法具有更好的定位精确度。

