基于远洋渔船作业场景的机会网络移动模型
陈成明, 虞丽娟, 凌培亮, 曹守启
(1.同济大学 机械与能源工程学院,上海 201804; 2.上海海洋大学 工程学院,上海 201306; 3.国家远洋渔业工程技术研究中心,上海 201306)
机会网络(Opportunistic Networks,简称ON)作为一种间歇式联通网络环境下依靠节点移动带来接触机会进行信息通信的手段,更适合实际的自组网需求,对未来的普适计算具有重大影响,近几年来受到越来越多学者的关注[1-6].机会网络利用节点移动形成的通信机会以“存储-携带-转发”的路由模式实现通信,能够处理网络分裂、时延等已有无线网络技术难以解决的问题,主要应用于缺乏通信基础设施、网络环境恶劣的场合[7],如偏远地区网络传输、车载通信、野生动物追踪、便携式设备组网、紧急突发场合等[8].由于机会网络的传输机会有赖于节点移动,不同移动模型对机会网络的网络性能有着不同的影响[9].文献[10]研究了不同类型移动模型的适用场景及对机会网络路由协议仿真的影响,同一路由协议在不同移动模型下的消息传输率和平均时延有大幅变化,需要根据路由协议应用场景选择合适的移动模型.在远洋渔船机会网络(Ocean Fishing Vessel Opportunistic Network,简称OFVON)中,渔船节点稀疏、节点移动规律复杂、场景范围大,对网络的性能要求更高,为保证网络稳定、高效的运行,需对网络进行运行前的静态规划和运行中的动态拓扑重构.而实际的网络运行数据很难获得,静态规划只能通过模拟仿真完成,仿真中的移动模型是否符合实际的场景,将直接影响静态规划结果.而现有的移动模型主要针对野生动物、人群和车辆组网建立的,无法准确描述渔船节点移动的特性.事实上,很难找到一个合适的移动模型完全适合远洋渔船作业时移动的场景,现有的这些移动模型只适用于一种或几种场景,无法适应所有场景.如果将这些模型直接应用于OFVON中,不仅无法表示OFVON中渔船节点移动的特征,而且直接影响仿真结果的合理性.因此,移动模型是否合理对路由协议中相关参数的设计具有举足轻重的作用.
现有移动模型分为个体移动模型和群组移动模型两类,文献[11]对机会网络的移动模型进行了详细的分类和阐述.对于移动模型的研究主要有两种途径,一是基于解析模型进行理论或仿真分析,经典的移动模型主要有RW(Random Walk)模型[12]、RWP(Random Way Point)模型[13]、RD(Random Direction)模型[14]、SRM(Smooth Random Mobility)模型[15]、GM(Gauss-Markov)模型[16]和SMS(Semi-Markov Smooth)模型[17]等;另一种研究途径是基于真实运动轨迹集来进行统计分析,比较著名的项目有MIT 的Reality Mining项目[18],UCSD的Wireless Topology Discovery项目[19]等.
在上述这些用于仿真的移动模型中,SMS模型目前应用最为广泛,它融合了SRM模型和GM模型的特征,认为节点一次完整的运动由加速、匀速、减速和静止4种状态组成,并在匀速状态中增加了高斯扰动,但不能很好地描述速率变化较小且有较大转弯的场合,对于加速结束后运动规律变化复杂的场合也很难描述.
一种好的移动模型要具有两个重要的特征:① 实体节点的运动为平滑运动,即节点的速率和方向具有时间相关性,不会发生大的突变;② 平均速率平稳,不会随着时间的延长发生衰减.
因此,本文研究了一种考虑渔船移动特征的平滑转弯的半马尔科夫移动模型(Smooth Turn Semi-Markov Smooth Mobility Model,简称STSMS模型),使其仿真结果更接近现实的渔船作业时的运动情形.
1 SMS模型
SMS模型是对RD模型进行了改进,使之更符合现实的移动场景.SMS模型基于平稳运动的物理规律进行建模,一个典型的SMS模型移动由3个连续的移动阶段和一个暂停阶段(p-阶段)组成,移动阶段包括加速阶段(α-阶段)、匀速阶段(β-阶段)和减速阶段(γ-阶段).连续时间的SMS随机过程可用一个迭代的4状态转换过程(Transition Process)来表示,如图1所示.
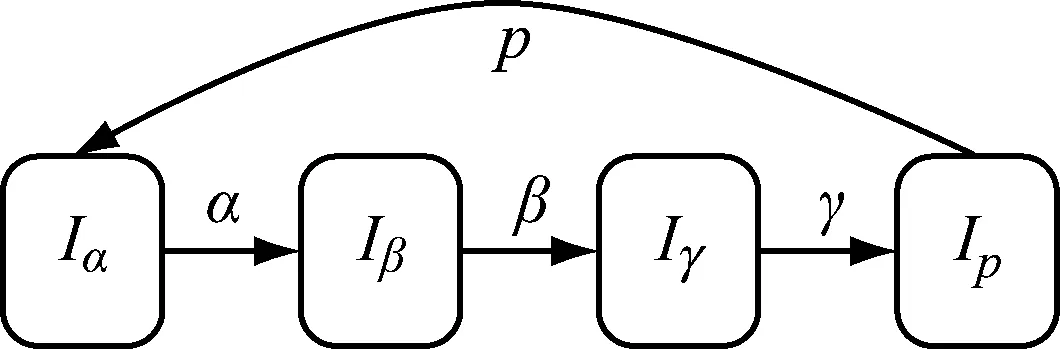
图1 SMS模型4状态
用I表示SMS模型的状态空间,即I={Iα,Iβ,Iγ,Ip},这里I(t)表示节点在时刻t所处的状态.在SMS移动的随机过程中,{Z(t),t≥0}表示各个阶段进行转移的过程,由于在两个连续的移动状态之间的转移时间服从离散的均匀分布,且该移动过程符合平滑移动的物理法则,因此称之为半马尔科夫模型.在SMS模型中,虽然在匀速状态增加了高斯扰动,但对于速率变化缓慢且经常有大转弯的场合没有描述,因此,OFVON中的移动模型需要在SMS模型的基础上进行改进.
2 STSMS模型描述
根据渔船运动特点,将渔船节点移动模型的运动分为加速、高速稳速、减速、低速稳速、转弯、减速和暂停7个阶段,7个阶段用来描述一次完整渔船作业过程的7种状态.与原SMS模型不同的是,本文提出的STSMS模型,渔船在上一作业结束后开始加速航行,当速度达到目标经济航速时,渔船开始以较高的航速稳速航行,由于海域面积广,短时间内渔船近似以某一方向(航向)直线航行.当发现鱼群(或某一计划作业海域)开始作业时,渔船开始减速,直到速度达到作业航速(某一较低的航速)时,开始以较低的航速稳速航行进行作业,作业一段时间后,如需要拖网、拉网等作业时,将进入转弯阶段,在整个作业过程中,可能需要多次转弯.当作业结束后,渔船进入短时间的减速和暂停状态,进行休整,然后开始加速航行,进行下一个循环.定义:STSMS模型包括加速、高速稳速、减速、低速稳速、转弯、减速和暂停7个运动状态.则该移动模型的随机过程可看成是一个迭代的7状态转移过程.用I表示模型的状态空间,I={Iα,Iβ,Iχ,Iγ,Iε,Iη,Ip},I(t)表示节点在时刻t所处的状态.7个运动阶段的移动模型如图2所示.
7个阶段的集合定义为S={α,β,χ,γ,ε,η,p},Δt表示时隙,时间以Δt进行划分,为了简单,将Δt标准化为1.下面对各个阶段进行具体描述.
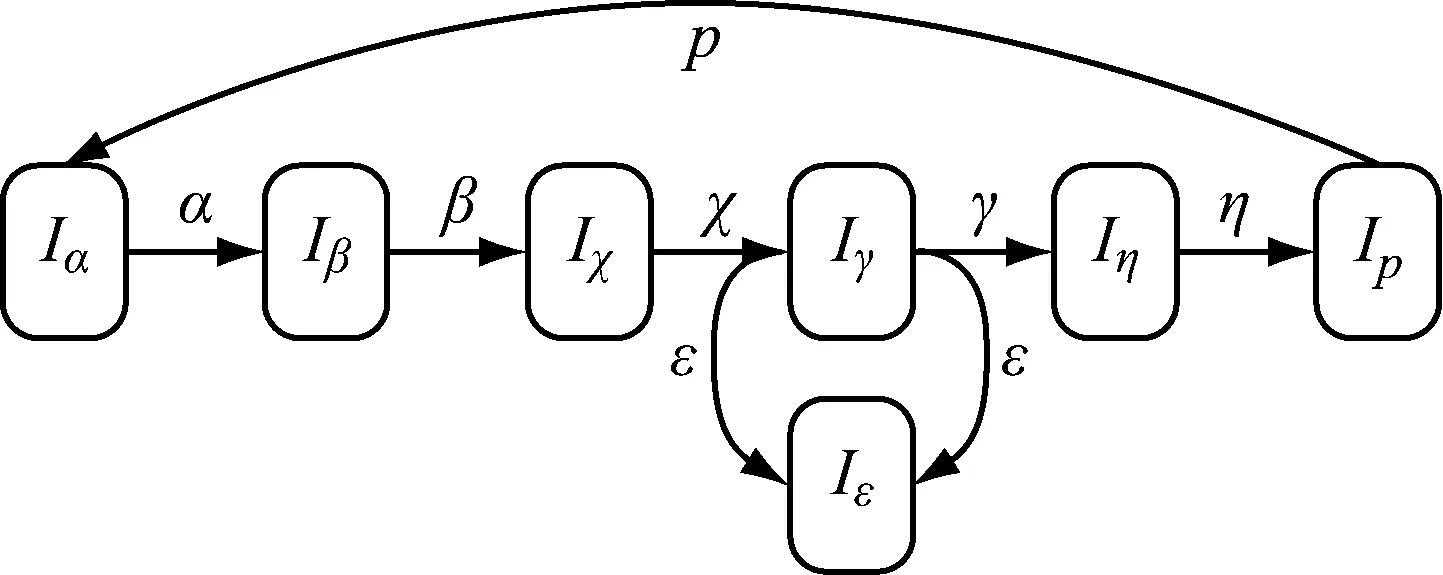
图2 远洋渔船作业过程的STSMS模型
2.1 加速航行阶段(α-阶段)

2.2 高速稳速航行阶段(β-阶段)

(1)
(2)
在β-阶段结束时,渔船节点的航速和航向分别为
(3)
(4)

2.3 减速航行阶段(χ-阶段)

2.4 低速稳速航行阶段(γ-阶段)

(5)

(6)
在γ-阶段结束时,渔船节点的航速和航向分别为
(7)

(8)

2.5 转弯阶段(ε-阶段)
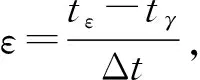
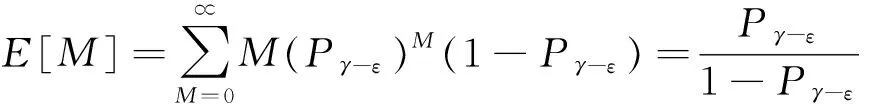
(9)
2.6 减速航行阶段(η-阶段)

3 STSMS模型节点运动方程
渔船在海面上航行,渔船节点的运动属于二维平面运动,通过建立节点的数学运动方程来详细描述渔船节点的运动状态,运动方程包括航速和航向的数学方程.根据上一节建立的渔船移动模型,把7个不同的阶段分成两组,航速不变的一组和航速一直发生变化的一组:①{α,χ,η},速率一直发生变化;②{β,γ,ε,p},速率不变.
首先建立笛卡尔直角坐标系,如图3所示.

图3 渔船节点运动直角坐标系
渔船节点的航速为v,航向为φ,可得
(10)
那么,对于①组,假设节点处在{α,χ,η}中某阶段的某个初始时刻t0,此时所处的位置为(x0,y0),节点的航速大小为v0,航向为φ0,节点的加速度为a,那么,经过l个时隙,节点在时刻tl的位置如下:
(11)
式中,a>0表示节点处于加速航行阶段;a<0表示节点处于减速航行阶段.对于第②组,节点处在{β,γ,ε,p}中的某个状态下,假设已知节点在第l个时隙的运动状态参数,位置为(xl,yl),航速为(v,φl),那么第l+1个时隙对应的节点位置为
(12)
当ω=0时,节点以固定航速匀速航行;当ω≠0时,节点以固定航速在海面上匀速转弯,ω的大小和正负表示转弯的大小和左转右转.
4 STSMS模型平均速率稳定性分析
由于RWP 模型无法进入平稳状态,即节点的平均速率会随着时间而不断地衰减[20],为了实现渔船移动模型具有平均稳态速率不随时间改变的特性,这里设定渔船移动模型的初始速率E[vini]与平均稳态速率E[vss]相等.
假定各个阶段速度的期望用EIm[v],m∈S表示,各个阶段的时间期望用EIm[t],m∈S表示,令π=(πα,πβ,πχ,πγ,πε,πη,πp)为STSMS移动模型下的各状态时间平稳分布,则
(13)
式中:E[Tm]表示渔船节点一次作业过程中m阶段的期望时长;E[T]表示一次作业过程中运动的全部时长;E[Tp]表示暂停阶段的时长.对于m取{α,β,χ,η,p}中的某个阶段,渔船节点一次完整作业过程这些阶段出现的次数智能为1,对于m取γ-阶段和ε-阶段,根据之前分析,γ-阶段和ε-阶段的次数分别为M+1次和M次.可得
(14)
E[T]+E[Tp]=E{α}+E{β}+E{χ}+
(M+1)E{γ}+ME{ε}+E{η}+E{p}
(15)
4.1 初始状态下的平均速率E[vini]分析
E[vini]可以表示为
E[vini]=E[E(vini)|Im]=παEIα(v)+πβEIβ(v)+πχEIχ(v)+πγEIγ(v)+πεEIε(v)+πηEIη(v)+πpEIp(v)
(16)
由STSMS模型描述可得
(17)
由式(13)~式(17)可得
E[vini]=

(18)
4.2 平均稳态速率E[vss]分析
定义W(t)表示渔船节点从初始时刻t0到时刻t期间渔船运动的时隙数,Wp(t)表示渔船节点处于暂停状态的时隙数.T(i)表示第i-1次运动到第i次运动转换所需要的时间,N(t)表示模型的更新次数,Tp(i)表示暂停的时间.
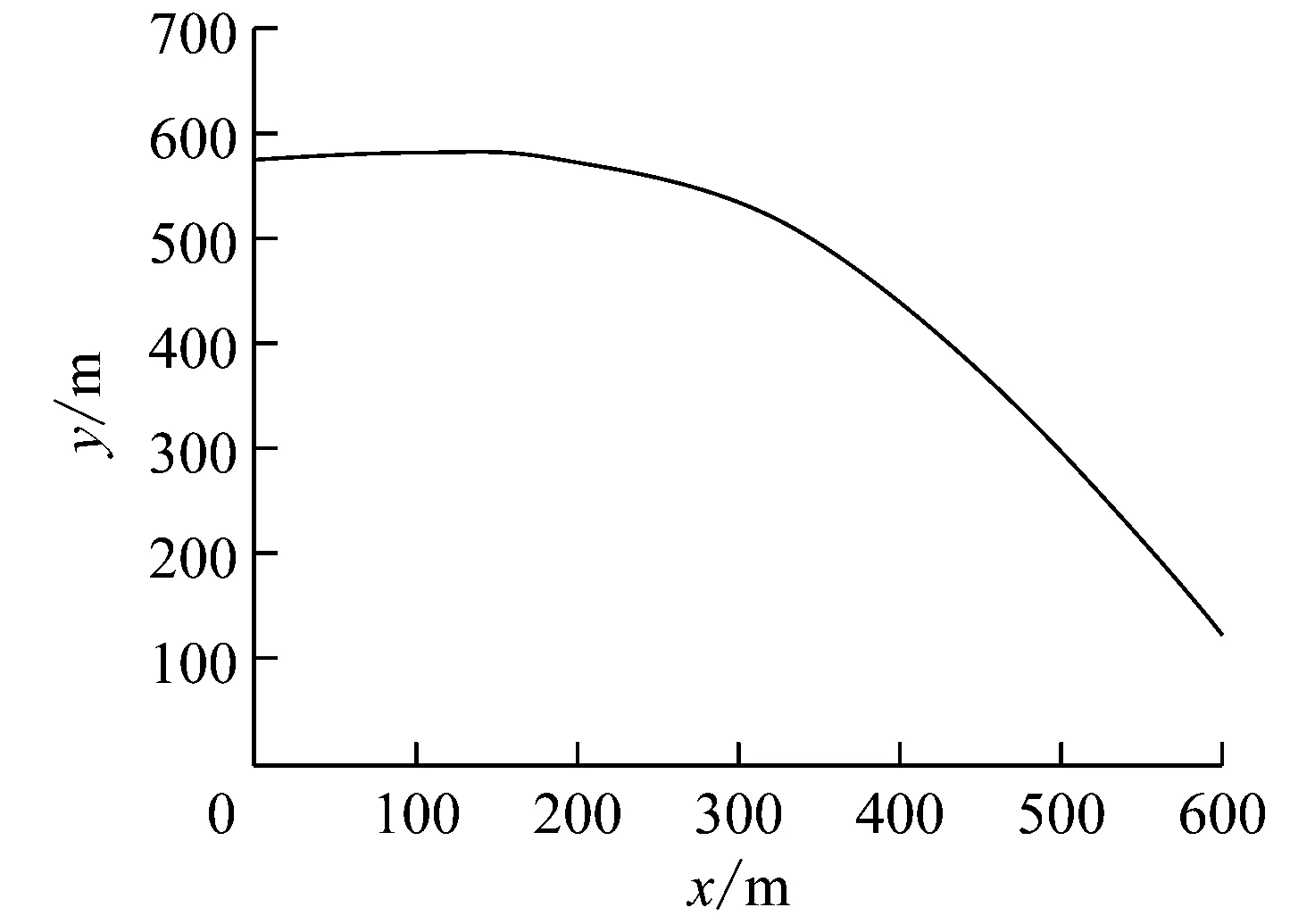
当t→∝时,有N(t)→∝,其累计分布函数可通过vss (19) 式(19)中,1{}表示满足大括号内的条件时取1,不满足取0. 其中 (20) W(t)和Wp(t)满足关系如下: (21) (22) (23) (24) 式(23)、式(24)对v求导,可以得出平均稳态速率实际是由各个状态下的稳态速率组成,即 E[vss]=Eα[vss]+Eβ[vss]+Eχ[vss]+Eγ[vss]+Eε[vss]+Ep[vss] (25) (26) 由式(25)、(26)推得 (27) E[vini]=E[vss],从而说明STSMS模型不会随时间发生衰减. 通过使用NS-2网络仿真工具,对渔船机会网络的节点移动模型进行仿真,并与RWP模型的性能进行比较.主要仿真参数设置如表1所示. 表1 STSMS模型参数设置 个体的随机移动模型能否较好地反映节点的运动规律关系到移动模型本身的可信度,同时也影响网络协议的仿真性能.因此,下面通过在仿真环境中验证所建立的移动模型具有和渔船节点运动轨迹相似的特性. 仿真过程中随机截取了不同节点运动时的位置,运动轨迹线如图4所示. 图4a描述了渔船从加速阶段到高速稳速航行阶段;图4b描述了渔船从低速稳速阶段结束后,进入了减速阶段,然后进入了短暂的暂停阶段;图4c描述了渔船的转弯航行状态.从图4可以看出,移动模型仿真了渔船从开始加速到暂停7个阶段的完整运动过程,实现了渔船真实航行运动轨迹的模拟. a b c 另外,从图4可以看出,渔船节点运动轨迹平滑,没有拐点和断点出现,基本符合远洋渔船机会网络节点移动模型的要求. 选择速率范围v∈[0,7]m·s-1,平均速率的期望值为3.5 m·s-1,对RWP模型的平均稳态速率进行仿真,结果如图5所示,随着仿真时间的延长,仿真的平均速率不断减小,与期望值的偏差越来越大,呈衰减的趋势,说明了RWP模型不能提供一个平稳速率而且有衰减. 图5 STSMS模型平均稳态速率 同样,对提出的STSMS模型的平均稳态速率进行仿真实验,实验参数配置按照表2所示.模型中所有节点都从α-阶段的第一步开始加速航行,每个阶段的持续时间范围[1-12]min,假定暂停时间为0,通过式27可知,STSMS模型的理论结果E[vss]=3.8 m·s-1. 图6 RWP模型平均稳态速率 图6给出了120 min的仿真时期内,理论值和STSMS-1的仿真值,在开始20 min时期内,由于所以节点都是从α-阶段开始加速,因此初始速率很小,在到达稳态速率前,有一个震荡的预热期.在20 min以后,STSMS模型的收敛于3.8 m·s-1附近,并保持稳定. 如果节点的初始阶段是在β-阶段或χ-阶段后的某一阶段,那么渔船节点将选择一个随机的初始步速度,在β-阶段的第一步为vα+1,在χ-阶段的第一步为vβ+1等,它们都均匀地分布在范围[vmin,vmax]上,由图6可以看出,STSMS-2仿真的平均速率从仿真一开始进很稳定.正如期望的那样,不管STSMS模型初始速率如何,其平均速率都不存在速率衰减问题.仿真的结果与STSMS模型基本吻合,从一个方面证明了该模型的合理性. 由于机会网络的发展目前还处在研究阶段,网络性能的评估还都依赖于移动模型进行仿真.本文分析了几种典型的移动模型,在此基础上,根据远洋渔船的移动特征提出了一种STSMS移动模型,具有加速、高速稳速、减速、低速稳速、减速和暂停7个状态,通过仿真,该模型与渔船的移动表现的特征非常相似,并且具有不随时间延长速度衰减的稳速特性,优于RWP移动模型.模型中的各个状态定义的参数可以独立调整,以适合不同作业类型的渔船和其它运动场景.本文提出的移动模型仅仅对运动轨迹和平均稳态速率进行了仿真,下一步将对模型的时间平稳分布和点空间分布均匀性进行研究,同时将该模型应用于机会网络路由协议中.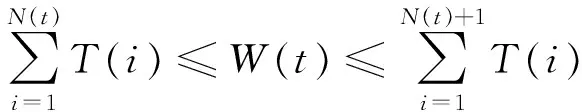


5 仿真与分析

5.1 运动轨迹线


5.2 平均稳态速率


6 结语

