半刚性连接梁柱式木结构抗侧力性能研究
刘应扬, 张 枫, 熊海贝
(1.郑州大学 土木工程学院,河南 郑州 450001;2.同济大学 土木工程学院,上海 200092)
梁柱式木结构的连接节点,无论是传统的榫卯连接,还是采用金属连接件的现代木结构节点,均具有一定的传递弯矩的能力,但是木材(与混凝土、钢材相比)特殊的材料性质和连接方式使节点难以达到完全传递弯矩的刚接连接的要求[1-3].对于含有半刚性节点的梁柱式木结构框架,其节点的半刚性特性是影响框架结构抗侧力性能的重要因素.
由于木结构节点难以达到刚接的要求,因此现阶段的设计方法通常将节点假定为铰接连接来计算结构的内力,进而进行构件截面和节点连接的设计;同时,设置支撑、剪力墙等抗侧力构件,以满足整体结构抗侧力要求;结构的耗能和延性性能,由支撑、剪力墙或者其他附加构件(如阻尼器)提供和实现.但此设计方法也有相应的弱点和不足之处.半刚性的节点在实际结构中会承载一部分的弯矩,节点在弯矩作用下易产生横纹方向的拉应力和顺纹方向的剪应力,这两者也是木材材性中最薄弱的环节,可能导致节点区域木材的开裂[4],甚至结构节点的失效,而铰接设计方法则缺少相应的计算,在节点连接处的设计可能会偏于不安全.
现代木结构发展应用的方向是高层和大跨结构,结构的变形控制至关重要,设计中对节点力学性能把握的要求也进一步提高,基于半刚性节点假定的设计方法有必要进行研究和推广.半刚性框架的计算分析较早应用在钢结构设计中,用于考虑双腹板角钢连接、上下翼缘角钢连接、T形键连接等难以达到刚接要求的梁柱节点设计.在结构内力计算中,多采用通用有限元程序,以弹簧单元模拟梁柱节点的力学特性,输入弯矩-转角关系,进而得到外力作用下结构的响应[5];一些学者也采用理论分析的方法,建立基于半刚性节点的单元刚度矩阵,结合数值计算方法求解,这种方法本质上和采用有限元程序建模计算是一致的[6-7].有限元计算方法的分析过程较为隐性,难以得到问题的解析解,不利于从总体上把握结构的性能;因此,也有学者在保证框架为“结构”(假定全部或部分的半刚性节点为刚性节点)时,借助结构力学的方法进行内力求解,之后再考虑半刚性节点的受弯转动,线性叠加得到结构的总体位移反应[8-9];该类方法可以得到相关问题的解析公式,能够定性和定量地研究结构的位移组成以及各参数的影响,但在内力计算时,并没有考虑半刚性节点对结构内力分配的影响,导致研究结果不够精确.
针对现阶段设计方法和研究手段上的不足之处,本文拟采用结构分析的方法,对梁柱节点、柱底节点均采用半刚性的假定,进而对梁柱式框架的抗侧力性能进行理论分析.同时,开展螺栓连接木结构框架结构、梁柱节点的抗侧、抗弯试验,研究半刚性框架、节点的传力机理和破坏模式.最后,基于获得的试验数据对本文推导的理论公式进行验证.
1 半刚性框架抗侧力理论分析
半刚性框架的力学计算模型可以按图1简化,图中:L为框架跨度;H为框架高度;Eb、Ec为梁、柱构件顺纹弹性模量;Ib、Ic为梁、柱截面的惯性矩;Kφ,c为柱底节点的转动刚度;Kφ,b为梁柱节点的转动刚度.不考虑竖向荷载,结构在水平力F作用下的弯矩示意图如图2所示.

图1 半刚性框架力学计算模型
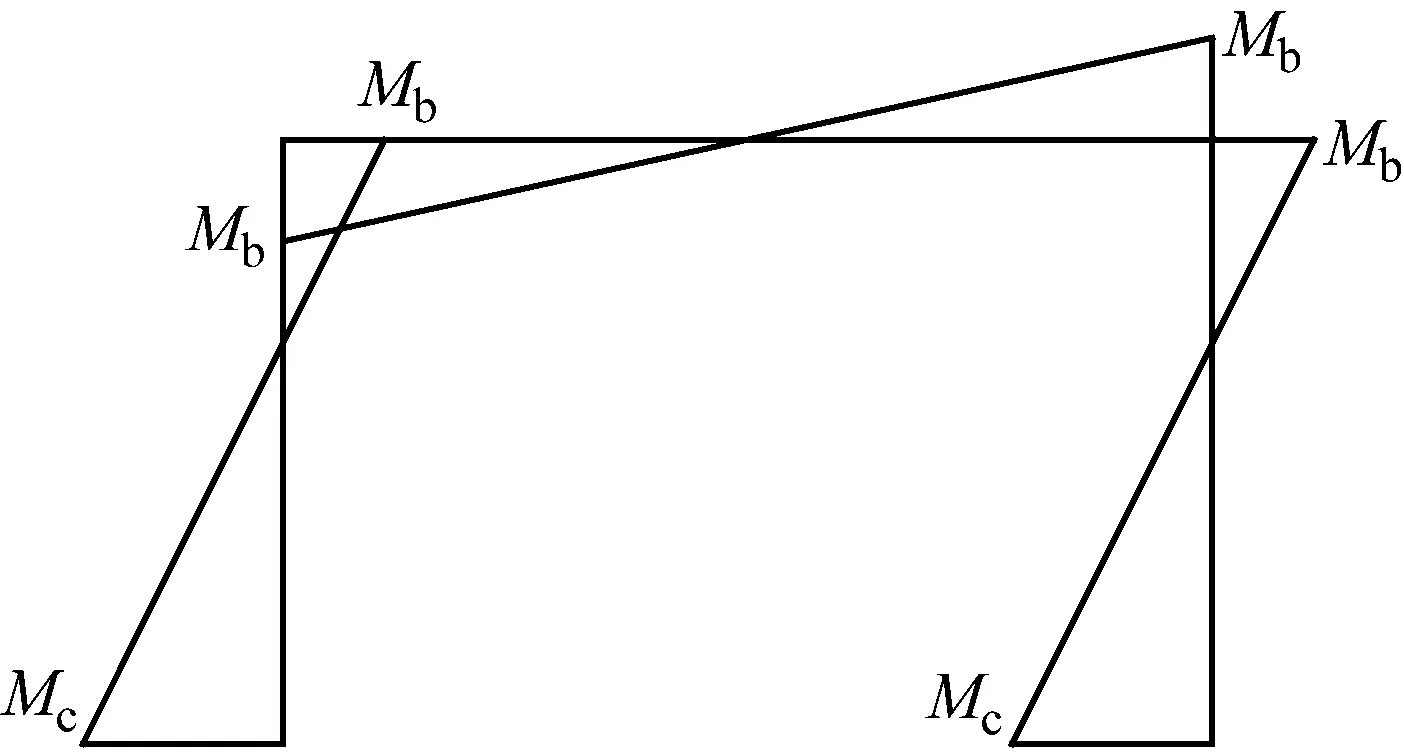
图2 侧向力作用下的弯矩示意图
图中梁柱节点的弯矩为Mb,柱底节点的弯矩为
(1)
单独将柱作为隔离体分析,如图3所示.

柱上弯矩以框架内侧受拉为正,可以表示为
(2)
不考虑柱剪切变形的影响,柱上任一微端y处(0≤y≤H)的曲率w″(y)为
(3)
将式(2)代入式(3)中,则柱曲率表示为
(4)
式(4)积分后可以得到柱转角、柱挠度的表达
(5)
A1y+A2
(6)

因此,式(5)和式(6)可以更新为
(7)
(8)
单独将梁作为隔离体分析,如图4所示,同理可以得到梁转角和挠度的表达,如式(9)、式(10)所示.
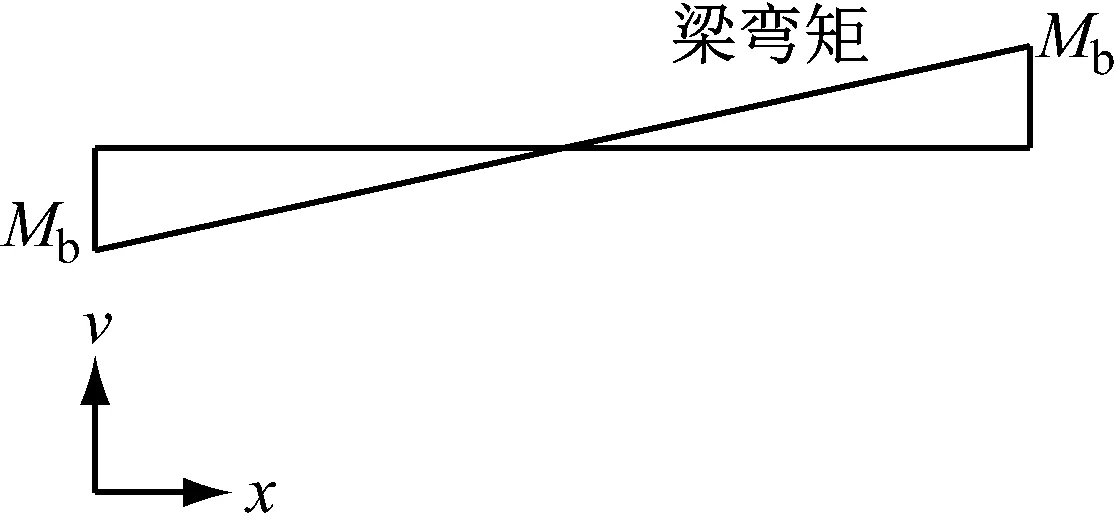
(9)
(10)
在柱顶(y=H)和梁端(x=0),根据变形协调,可以得到
(11)
因为θ(H)、β(0)均为负值,故
(12)
将式(7)、式(9)代入式(12),可解得
(13)
(14)
结构的内力可以按式(13)、式(14)计算,将计算结果代入式(7)—式(10)可以计算得到结构中任一点的转角和挠度.结构在侧向力作用下的位移,可以表达为柱顶的挠度的绝对值,即
(15)
因此,结构的抗侧刚度可以表达为
(16)
由此可见,半刚性框架的抗侧刚度由梁、柱构件的线刚度和梁柱、柱底节点的抗弯刚度共同决定,节点的半刚性特性直接影响结构的抗侧力性能.为简化设计计算,式(16)可以整理为
(17)

为验证理论推导的正确性,分别令梁柱、柱底节点的刚度趋于0或∞,得到框架内力的计算结果,并与结构力学计算结果相比较.
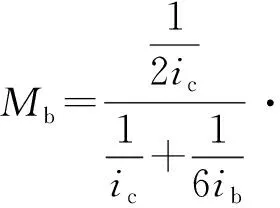
2 螺栓连接木框架抗侧力性能试验
2.1 试验概况
共设计3榀单层单跨梁柱式木框架足尺试件,跨度均为4 110 mm,高度均为2 740 mm,跨高比为3∶2.梁截面为280 mm×180 mm、柱截面为280 mm×230 mm,材料均采用层板胶合木,木材均为加拿大进口的云杉-松-冷杉规格材,材质等级为IIc级,由苏州皇家整体住宅系统股份有限公司进行胶合,胶合后的强度等级为TC11A,通过材性试验[10]得到木材的顺纹受压弹性模量为9 542 MPa、横纹受压弹性模量为334 MPa.梁柱节点、柱脚节点均采用螺栓-钢插板做法,其中螺栓采用6.8级普通螺栓、直径14 mm,钢板采用Q235钢、厚度10 mm.试件示意及节点详见图5.

a 梁柱框架示意图

b 柱底节点详图

c 梁柱节点详图
试验在同济大学土木工程防灾国家重点实验室进行,采用申克加载系统进行单调和低周反复加载,如图6所示.申克机施加推力时,通过左侧钢板直接传力到试件;施加拉力时,先通过钢拉杆传力至右侧钢板,再由右侧钢板传力到试件,从而避免试件节点的局部拉坏.安装在龙门架上的钢滚轴用于限制试件平面外的变形.柱底钢板与地梁采用8个M22螺栓连接,地梁与实验室水泥台座牢固固定.

图6 梁柱框架试验加载装置示意
单调加载制度和低周反复加载制度,分别参考美国材料与试验协会(ASTM)的E564[11]和E2126[12],采用位移控制加载.试件载力下降至极限荷载的80%时或结构侧向位移达到250.0 mm(层间位移角约为1/11,结构已不宜继续承载)时,试验终止.
2.2 试验现象及破坏模式
本文以低周反复试验的加载过程,对试验现象及破坏模式进行说明.试验中随着侧向位移的增加,梁柱节点表现为局部顶紧.在侧向位移加载至50 mm(1/55位移角)时,柱底节点首先出现了裂缝;梁端木材在侧向位移约为100 mm(1/27位移角)时,也发生了劈裂.在后续的试验中,柱底和梁端的木材裂缝继续开展,见图7,但结构的承载力并没有显著下降,试验在达到位移失效限值250 mm(1/11位移角)时终止.

a 梁柱框架整体变形及破坏示意

b 柱底节点破坏情况

c 梁柱节点破坏情况
纯框架结构体系在试验中表现出“弱节点、强构件”的破坏模式.这是因为当结构受到侧向荷载时,半刚性的节点承受一定的弯矩,从而使节点处木材出现横纹拉应力和顺纹剪应力;而节点区域的顶紧,导致木材局部的应力集中,增大了横纹拉应力和顺纹剪应力,而这两者也是木材材性中最薄弱的环节,因此导致节点处的过早开裂破坏.在试验后对节点区域进行了拆解,发现螺栓杆均出现了弯曲屈服,部分螺栓杆甚至出现了弯曲折断,说明螺栓在结构受到往复力时提供了能量消耗.
虽然纯框架结构体系表现出了节点区域过早的劈裂破坏,但是整体结构的变形能力很强,并未出现承载力的急剧下降和倒塌现象.
3 梁柱螺栓连接节点抗弯性能试验
3.1 试验概况
梁柱节点采用与第2节中框架节点相同的设计,木材、螺栓、钢板的材料和规格也均保持一致,节点详图如图5c所示.共设计5个梁柱节点足尺构件,3个为单调加载,2个为低周反复加载.
试验在同济大学木结构试验室进行,加载装置采用双通道电液伺服加载系统.为便于加载,将胶合木柱水平固定于加载梁上,通过作动器在梁端施加水平荷载,试验加载如图8所示.

图8 梁柱节点试验加载装置示意
单调加载制度参考ASTM D1761[13],低周反复加载制度参考ASTM E2126中方法C给出的CUREE加载制度[12].节点所承受的弯矩等于木梁端部的水平力与加载点至螺栓群中心距离的乘积,最终,得到构件的转角-弯矩曲线.
3.2 试验现象及破坏模式
本文以低周反复试验的加载过程,对试验现象及破坏模式进行说明.试验开始后断续出现由于组件之间的错动和木梁柱之间挤压造成的噼啪声.当梁柱相对转角达到6°左右时,木梁上开始出现裂缝,并伴随着巨大的木材开裂声.这些裂缝通常首先在受拉侧外排螺栓处出现,同时受压侧外排螺栓处也出现裂缝.节点区域木材首先从螺栓孔附近开裂,随变形加大沿木纹向木梁与柱接触端逐渐扩展.最终,由于木材的横纹受拉和顺纹受剪共同作用,节点的裂缝主要表现为顺纹劈裂,伴随有少量的列剪切破坏模式,见图9a.
拆开木构件,见图9b,可以发现,木柱上的螺栓变形很小,几乎没有弯曲;木梁上的螺栓出现了明显的弯曲变形,在与钢板的承压处出现了一个塑性铰,塑性铰以外的部分基本刚直.同时由于螺栓的弯曲变形,在木构件的外表面及与钢板接触的内表面都出现了木材承压破坏.值得注意的是,木梁的受拉和受压侧螺栓的弯曲程度和木孔的承压破坏程度并不相同,受拉侧的破坏更加明显,这是因为在受压侧,梁柱之间的承压分担了部分荷载;在挤压处,木柱上也出现了压溃破坏.

a 节点开裂情况

b 螺栓变形情况
4 半刚性框架抗侧力性能计算
通过试验研究,获得了梁柱框架的抗侧力位移-荷载曲线,以及梁柱节点转角-弯矩曲线,如图10和图11所示,主要力学性能参数见表1.
基于之前推导的理论公式,结合试验确定的梁柱节点的力学性能,本节拟对半刚性框架的全过程力-位移关系进行计算,见图12,并与框架试验结果进行对比,验证本文理论研究的合理性与实用性.
图中函数g为节点半刚性特性的表达,梁柱节点的半刚性特性通过本文试验结果的平均曲线确定,柱底节点的半刚性特性通过有限元数值模拟确定[14],gb、gc的函数曲线如图13所示.结构全过程力-位移关系函数f的计算方法,可以通过以下计算步骤确定.

图10 梁柱框架试验结果
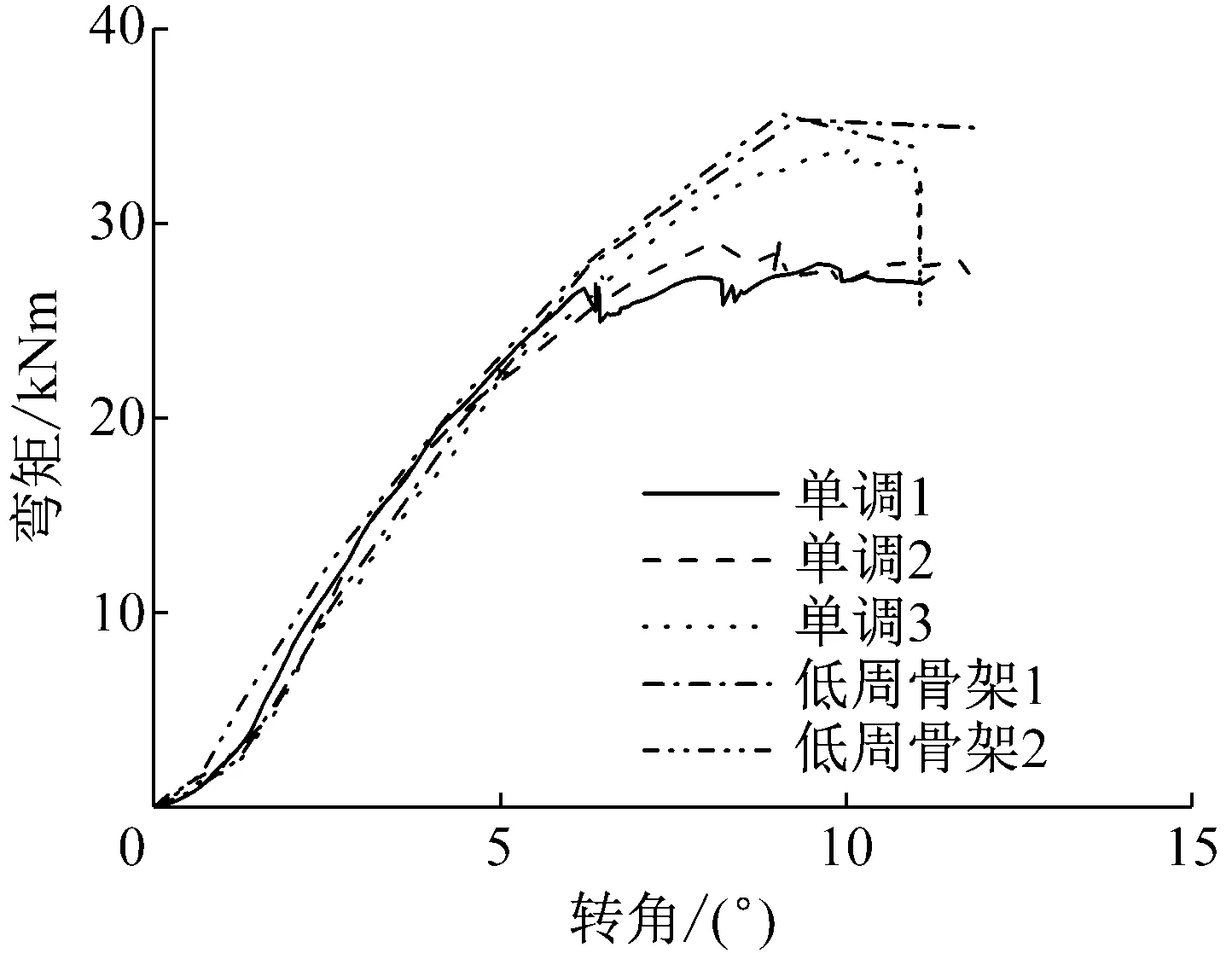
图11 梁柱节点试验结果

表1 试件主要力学性能参数

图12 节点受力状态和结构位移的对应关系

图13 gb、gc 函数曲线
(1)定义结构的初始状态
定义结构的初始状态:位移为Δ0、结构受力为F0、柱底节点转角为φc,0和梁柱节点转角为φb,0,通常初始状态下结构的位移和受力均为0.
根据函数g(对函数g求导,即根据函数曲线得到该点处的斜率),确定节点在转角φc,0、φb,0时的转动刚度Kc,0、Kb,0.由梁、柱尺寸和截面信息,得到线刚度ic、ib,结合该状态下节点的转动刚度Kc,0和Kb,0,通过式(16)计算得到该状态下结构的抗侧刚度Ks,0.
(2)定义结构基本增量
取柱底节点的转角增量作为结构的基本增量,为dφc.
(3)计算结构其他增量
当增量足够小时,柱底节点的弯矩增量可以按dMc=dφcKc,0计算.设结构受力的增量为dF,则梁柱节点的弯矩增量仍可按式(1)计算,即
(18)

(4)确定结构的下一状态
结构经历增量后达到下一状态,位移Δ1=Δ0+dΔ,结构受力F1=F0+dF,柱底节点转角φc,1=φc,0+dφc,梁柱节点转角φb,1=φb,0+dφb.该状态下,节点的刚度可根据函数g在φc,1,φb,1处切线斜率得到,即Kc,1,Kb,1,再根据式(16)确定该状态下结构的抗侧刚度Ks,1.
(5)循环步骤(1)~(4)求解,得到结构的全过程力-位移关系曲线,并获得节点受力状态和结构位移的一一对应关系.采用柱底节点转角等增量(取dφc=2.4×10-4rad),结合软件MATLAB计算得到框架结构的全过程力-位移关系曲线,与木结构框架试验结果对比,见图14.
从图14中可以看出,理论计算曲线与试验曲线有较好的吻合程度,理论计算曲线的刚度略低于试验结果,这是因为试验中设置的钢拉杆系统导致的,加载钢板在一定程度上限制了梁柱节点的开裂,延缓了结构刚度的退化.试验中,框架在加载至250 mm侧移时,由于位移较大而终止了试验,从理论计算结果中可以看出,在250 mm之后框架仍能维持其承载力至较大的位移,这与第2节试验终止前的现象具有相互印证之处.

图14 理论计算曲线与试验曲线对比
在工程中可以预先进行节点试验或数值模拟研究,确定节点的抗弯特性,而后通过本文推导的理论公式来预估框架结构的刚度和承载力,从而进行半刚性框架的抗侧力设计.
5 结论
通过对半刚性连接梁柱式木结构的抗侧性能进行了理论分析和试验研究,得到以下主要结论:
(1)节点连接假定为铰接,是当前木结构设计中广泛采用的一种假定,但是,木结构节点具有一定的半刚性能力,在框架结构中会承载一部分的弯矩,可能会引起节点区域木材的开裂,甚至导致结构节点的失效,因此,建议在设计中考虑节点的半刚性转动能力.
(2)试验研究表明,螺栓-钢插板连接的木结构节点,具有传递弯矩的能力,表现出明显的半刚性特性;在框架试验中,结构表现出“弱节点、强构件”的破坏模式,这是木结构不同于钢结构、钢筋混凝土结构之处,在工程设计中应予以重视.
(3)基于本文理论分析,给出了确定半刚性框架全过程力-位移关系的方法,在工程中可以预先进行节点试验或数值模拟研究,确定节点的半刚性特性,而后通过本文推导的理论公式来预估框架结构的抗侧力性能.

