水平紧密接触品字形三圆管自然对流换热的数值模拟*

石宏岩，刘 捷，卢文强

(中国科学院大学工程科学学院， 北京 100049) (2017年7月20日收稿； 2017年10月20日收修改稿)

表1 竖直排列多圆管结构的研究现状Table 1 Research status of vertical arrangement multi-cylinders structure

上述研究中，缺乏圆管之间间隙为零这样一种极限情况，即无间隙紧密接触。现在的换热器、核反应堆堆芯、高射炮炮管、枪的弹管普遍存在多圆管紧密接触这种极限情况，如图1所示。紧密接触多圆管的换热特性目前还缺少全面、详细的研究，没有一个适用范围较强的经验公式。基于圆管自然对流换热的研究现状，并考虑其对于工业和军事的重要性，有必要对紧密接触品字形三圆管的自然对流换热进行全面的研究，以便为相关工业和军事应用提供精确的经验关系式，为其设计和优化提供参考。该研究的难点在于广延空间所导致的计算区域非常大，所需网格数量过多给计算带来麻烦。为解决这个难点，在之前的研究中，本课题组采用Bejan等[13]提出的新计算模型，研究紧密接触水平和竖直排列双圆管的自然对流换热情况[14-15]。研究结果表明，此模型可以大幅减小计算所需区域的大小，节约计算成本，解决长期困扰自然对流领域研究的大空间、高计算量的问题。在该研究的基础上及受到紧密接触三圆管枪(图1)的启发下，本文研究水平放置紧密接触品字形三圆管(圆心成正三角形)在空气中的自然对流换热情况，研究范围为10≤Ra≤106。

图1 紧密接触品字形三圆管Fig.1 The gun with three attached cylinders

1 数理模型及计算方法

广延空间中物体绕流自然对流的研究一般是把所研究的物体放在一个足够大的人为设定的有限空间里，空间的边界对于该结构的流动传热需不施加任何的影响。因此，考虑把紧密接触品字形三圆管放在一个足够大的空间里，所有圆管都假设是定温的，其表面温度为一定值(Tw)，浸没在静止的空气中，周围空气的温度也设为一定值(T∞)，并且Tw>T∞。由于Tw>T∞，圆管附近的空气与圆管表面存在一定的温度梯度，圆管表面附近的空气会被圆管表面加热，由于气体的热膨胀，在圆管附近被加热的空气密度将会降低，导致热空气与远处的冷空气之间存在一个密度梯度，进而在空气中产生浮力，在浮力的推动下，空气围绕圆管流动发生对流换热。一般情况下，为了使人为所设定的有限空间边界不影响圆管的流动及热传递，计算区域往往是非常大的，相应的网格量就会很大。虽然一般圆管绕流问题都会假设流动Z方向上没有分量，将本来的三维问题简化为二维问题，但是计算量一般还是无法承受的。巨大的计算区域不仅会使计算时间成本巨大，而且也会限制研究所覆盖的Ra范围，使获得一个能在较大Ra范围内有意义的传热经验关系式变得非常困难。本文计算模型如图2所示，采用的方法是Bejan等[13]提出,假设流动是对称的，且是二维稳态的，重力方向为Y轴的负方向。另外，流体的热物性参数都用膜温Tm(=(Tw+T∞)/2)的值，且除Y方向动量方程中的密度项外，其余变量都假设与温度无关[14-15]。Y方向动量方程中的密度项假设仅随温度的变化而变化， 它们之间的关系可由Boussinesq近似假设表示：

ρ∞-ρ≈ρβ(T-T∞).

(1)

在密度变化只由温度变化引起情况下其定义是

式中：ρ是工质的密度，ρ∞是无穷远处的密度；β是体积热膨胀系数。显然，这个假设仅当区域中的温差很小时最为有效，小温差可以显著降低结果由热物性和β随温度变化而引起的误差。因此，为确保结果的准确性，本文中所有算例的温差都保持在1K以内。由于流动的温差极小，β可以按照理想气体方程，将其设定为β=1/Tm。

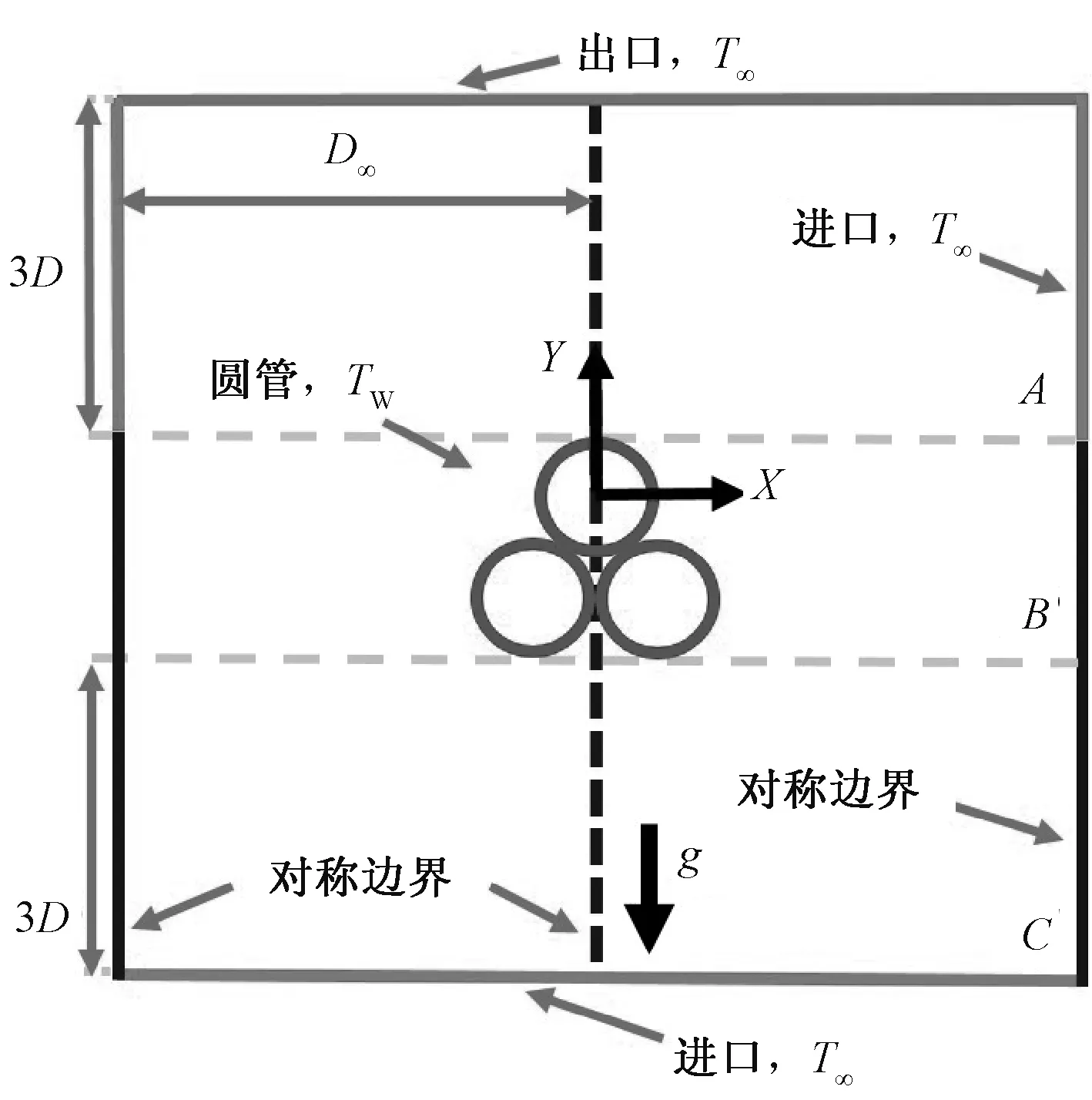
图2 模拟模型示意图及边界条件Fig.2 Schematic representation of the flow and the computational domain

假设工质是不可压缩的，并且忽略能量方程中的黏性耗散和辐射。控制方程组的数学表达式[1-3,13-15]如下所示，

本研究结果显示，常规康复治疗同时接受家庭腰椎稳定性训练联合肌内效贴治疗能更好地缓解腰痛，提高功能，改善患者的生活质量。腰椎稳定性训练联合肌内效贴治疗方法安全、简便、无创、疗效明确，在治疗慢性非特异性腰背痛方面值得推广。

连续性方程：

X轴的动量方程：

Y轴的动量方程：

能量方程：

由于流动是关于垂直中心线对称的，所以本文的计算区域只需选取一半(X>0)作为计算区域。其边界条件的具体设置及无量纲参数请参见文献[13-15]。

上述控制方程在ANSYSFluent(version15.0.0)里通过有限体积法被离散化。压力-速度耦合格式采用压力耦合方程组的半隐式方法SIMPLE联立求解，动量和能量方程中的对流项采用二阶迎风格式进行离散化。为了获得更加准确的结果，连续性、动量和能量方程的收敛标准都设定为10-6。然而，自然对流的传热计算往往是极难收敛的，想完全达到10-6的收敛标准其计算时间相当漫长。因此，本文将圆管表面的平均热流密度以及阻力系数作为收敛的判定标准进行输出监视，当这两个参数的值保留4位有效小数位数且不随迭代步数变化时，就认为区域内的流动及换热已经达到稳定。

在自然对流的数值研究中，网格是影响计算结果的一个重要因素，对其合理的划分可以得到准确的结果，减小网格数量，提高计算效率。图3是品字形三圆管计算的网格示意图，将其划分为两个区域，在圆管附近的区域I内，网格采用加密三角形非结构网格，有利于精确捕获边界层内的速度和温度的变化。而在边界层以外区域II则采用较稀疏的四边形网格，这样在不影响准确性的前提下，可以减少网格数量，进而提高计算效率。需要说明的是：本文三圆管附近两个网格之间的距离δ与圆管的直径D的比值，即为δ/D≤0.002 5,这样就能满足网格质量而且保证计算结果的准确性[13-15]。其中，A、B、C、D、E、F、O等点是为了后文分析方便表述而添加的。

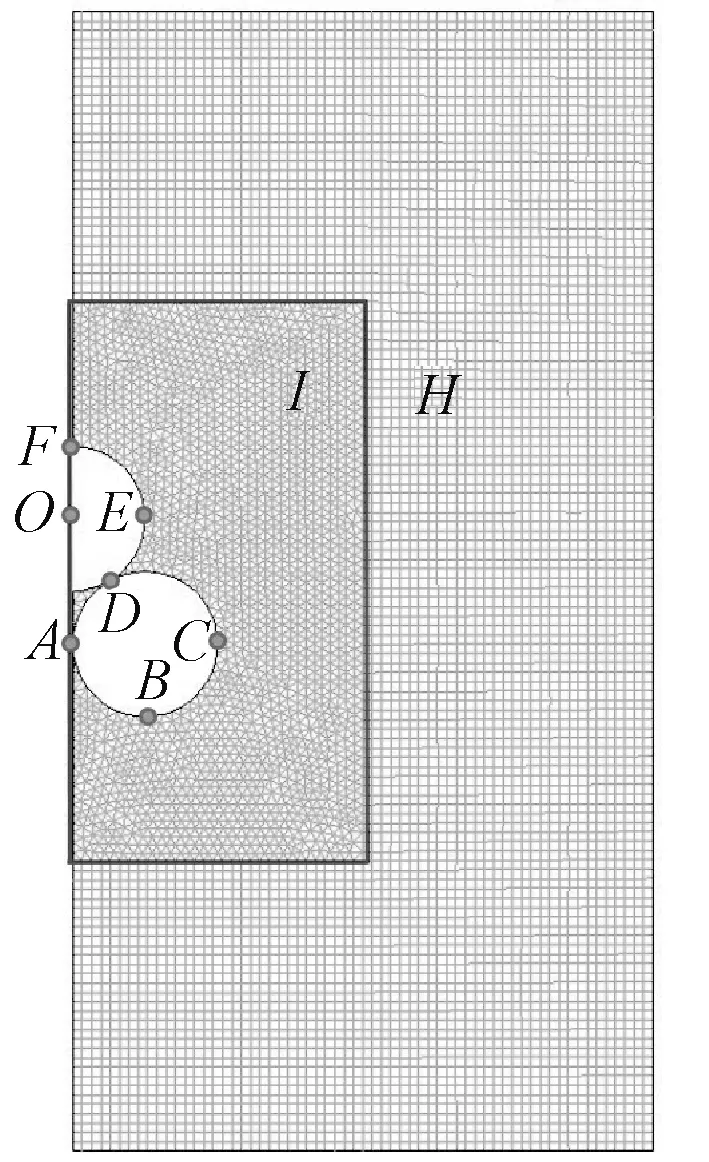
图3 计算区域的网格示意图Fig.3 Schematic representation of the computational grid

2 计算结果及分析

2.1 模型方法验证

图4 平均努塞尔数结果对比Fig.4 Comparison of average Nusselt number values with the previous results

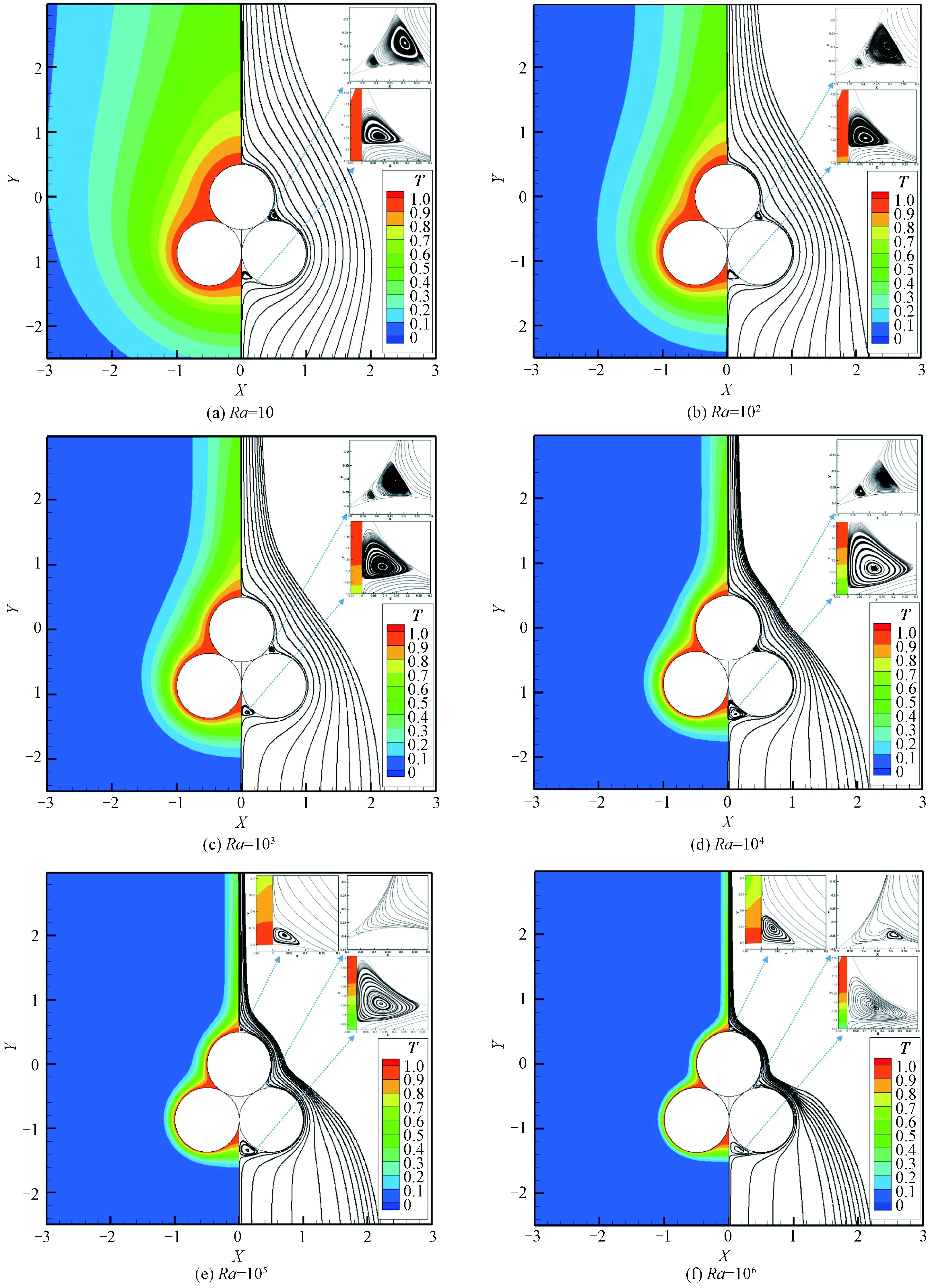
图5 在10≤Ra≤106圆管附近的温度场(左侧)和流线场(右侧)Fig.5 Isotherm contours (left half) and streamline (right half) in the vicinity of the cylinders for 10≤Ra≤106

2.2 温度场和流线场

在分析流动和传热问题的时候，借助于温度场和流线场可以很简单明了地表述研究问题的关键所在。图5是三圆管附近的温度场(左侧)和流线场(右侧)随Ra变化的图示，X、Y轴的数值是无量纲处理后的，图注中0～1是无量纲温度。总体而言，随着Ra的增大，换热方式由热传导逐渐向对流换热转变，对流流动逐渐增强，温度和速度边界层随之变薄。圆管下面的旋涡(A点附近)是由圆管表面上的滞止点和圆管之间的接触点引起的：在浮力的驱动下，流体沿着中心线向上流动，在前驻点处速度降为零，并伴随着压力升高。从这点开始，流体沿着圆管表面分流，其中一边的流体在流到接触点时改变方向，向上游流去，然而来流的作用使流体又不能向上游回流，在这种情况下，旋涡在接触点下方形成。而沿着圆管表面向另一方向流动的流体则继续保持附着在圆管的表面上。从前驻点开始，压力沿表面逐渐降低，流体在顺压力梯度的作用下逐渐加速。但是在D点附近，流动受到后方圆管的高温预热及阻挡影响，流动产生分离：一部分开始回流，导致此处产生回流涡；一部分沿着后方圆管表面继续流动，压力最终会降至最小值，在圆管的后部会产生逆压力梯度。此时流体开始减速，随着流体的减速，表面上的速度梯度最终会在圆管表面后部的某一位置变为零，这个点称为分离点。在该点，圆管表面的流体动量不足以克服逆压力梯度，边界层发生分离，并在下游形成尾流。在Ra=105和Ra=106时，在其后方产生分离涡，这与单圆管相同，但是在Ra较小的情形时，分离涡产生得不明显，这反映出流动的增强对分离点的影响，在相同Ra的情况下堆积三圆管的流动强度小于单圆管的流动强度。由于在三圆管的空隙交汇处，与外界通道并没有对流换热，该区域始终维持在高温情形下，无需展示其温度场和流线场。

2.3 局部努塞尔数

图6 在10≤Ra≤106时堆积三圆管表面Nuθ的分布Fig.6 Distribution of the local Nusselt number along the surface of the cylinders for 10≤Ra≤106

2.4 平均努塞尔数

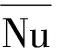
此拟合的曲线被绘制在图7中。公式的可决系数R2=0.999 3，表明拟合公式与数值模拟结果之间的拟合程度很好，因此可以确定所获取的经验公式可以为水平紧密接触品字形三圆管结构的自然对流换热提供工程计算所需要的精确预测，同时，其公式为无量纲的变化因素拟合得到的，普适性较强。

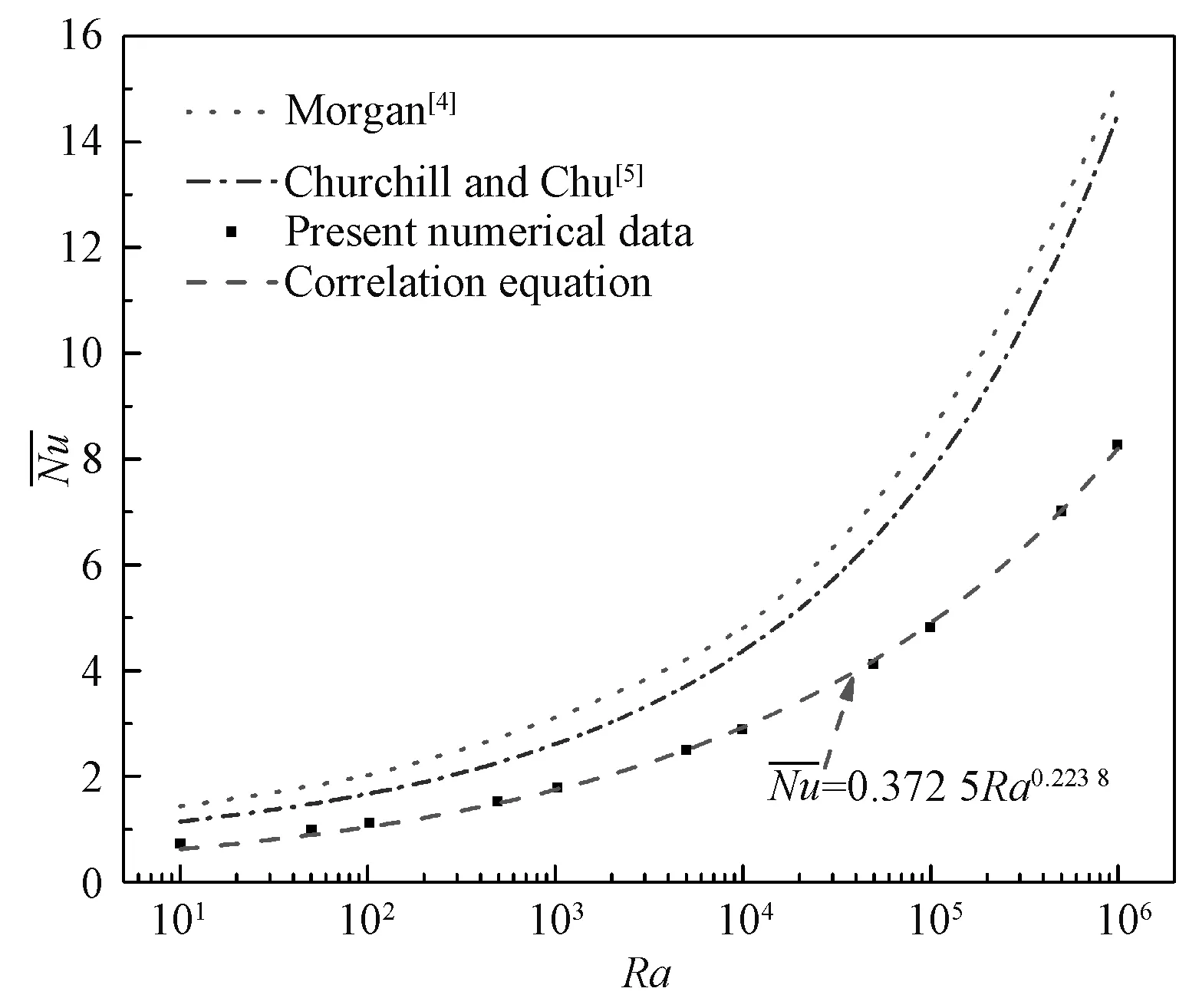
图7 模拟结果拟合的关系式和单圆管公式的比较Fig.7 The correlation for the present average Nusselt numbers and comparison of the obtained correlating equation with the previous correlations of single cylinder

3 结论

1) 随着Ra的增大，流动增强，对流换热能力增加，品字形三圆管的A、D点附近接触处的回流区也逐渐减小。在Ra=105和Ra=106的时候，在其后方产生分离涡，与单圆管相同，但是在Ra小的时候，产生的分离涡并不显著，这反映出流动的能力对分离点的影响。

2)Nuθ的峰值出现在140°附近，且数值大小随着Ra的增加而增大。由于回流涡的影响，A、D处换热能力趋近于0，分离点后分离涡处，由于受到羽流的影响换热能力也很弱。