中考中的反比例函数

葛春奎 潘晓花

一、一般的面积问题

在反比例函数y=[kx]（k≠0）图像中，过双曲线上任意一点引x轴、y轴垂线，所得矩形面积S=[k]或所得直角三角形面积S=[12][k].这是中考经常考查的一个知识点，体现了数形结合的思想.同学们做此类题一定要正确理解k的几何意义.

【例1】（2016·张家界）如图1，点P是反比例函数y=[kx]（x<0）图像上的一点，PA垂直于y轴，垂足为点A，PB垂直于x轴，垂足为点B，若矩形PBOA的面积为6，则k的值为 .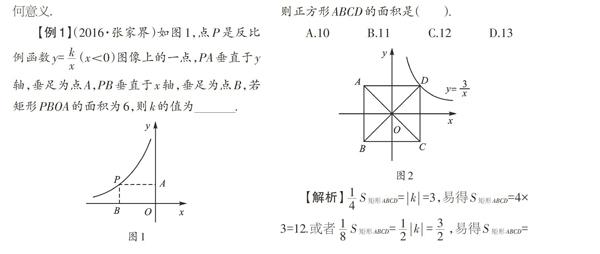

【解析】因为矩形PBOA的面积为6，可得[k]=6，因为反比例函数y=[kx]（x<0）的图像过第二象限，故k<0，答案为k=-6.

【例2】（2015·凉山州）以正方形ABCD两条对角线的交点O为坐标原点，建立如图2所示的平面直角坐标系，双曲线y=[3x]经过点D，则正方形ABCD的面积是（ ）.

A.10 B.11 C.12 D.13

【解析】[14]S矩形ABCD=[k]=3，易得S矩形ABCD=4×3=12.或者[18]S矩形ABCD=[12][k]=[32]，易得S矩形ABCD=8×[32]=12.故选C.

【例3】（2016·漳州）如图3，点A、B是双曲线y=[6x]上的点，分别过点A、B作x轴和y轴的垂线段，若阴影部分面积为2，则空白部分的面积的和S1+S2为 .

【解析】∵S1+S阴影=[k]=6，S2+S阴影=[k]=6，

∴S1+S2+2S阴影=12，

∵S阴影=2，

∴S1+S2=12-4=8.故答案为8.

二、与几何图形相结合的面积问题

【例4】（2016·云南）位于第一象限的点E在反比例函数y=[kx]的图像上，点F在x轴的正半轴上，O是坐标原点，若EO=EF，△EOF的面积等于2，则k=（ ）.

A.4 B.2 C.1 D.-2

【解析】因为EO=EF，△EOF的面积等于2，根据等腰三角形“三线合一”性质，可得[12]×2xy=2，解得xy=2，所以k=2.答案选B.

【点评】本题把反比例函数和等腰三角形结合在一起进行考查，没有图形.所以同学们首先要能够准确画出图形，再根据反比例函数k的性质和等腰三角形性质求解.

三、双反比例函数与几何图形相结合的面积问题

【例5】（2016·菏泽）反比例函数y=[ax]（a>0，a为常数）和y=[2x]在第一象限内的图像如图4所示.点M在y=[ax]的图像上，MC⊥x轴于点C，交y=[2x]的图像于点A；MD⊥y轴于点D，交y=[2x]的图像于点B.当点M在y=[ax]的图像上运动时，以下结论：①S△ODB=S△OCA；②四边形OAMB的面积不变；③当点A是MC的中点时，则点B是MD的中点.其中正确的个数是（ ）.

A.0 B.1 C.2 D.3

【解析】①正确.A、B两点都是y=[2x]图像上的点，根据反比例函数k的几何意义，可知S△ODB和S△OCA都等于[12][k]=1.

②正确.根据反比例函数k的几何意义可知：S矩形OCMD=[k]=a，S四边形OAMB=S矩形OCMD-S△ODB-S△OCA=a-2，所以不变.

③正确.如图5，连接OM，点A是MC的中点，则S△OAM=S△OAC.

∵S△OAM+S△OAC=S△OCM，

∴S△OAM=S△OAC=[12]S△OCM，

∵S△ODM=S△OCM，S△ODB=S△OAC，

∴S△ODB=S△OBM=[12]S△ODM.

∴点B一定是MD的中点.故选D.

【点评】本题对反比例函数k的几何意义的考查由浅入深，由单个反比例函数到双反比例函数，同学们需要正确理解反比例函数k的几何意义.

【例6】（2016·宿迁）如图6，在平面直角坐标系中，一条直线与反比例函数y=[8x]（x>0）的图像交于两点A、B，与x轴交于点C，且点B是AC的中点，分别过两点A、B作x轴的平行线，与反比例函数y=[2x]（x>0）的图像交于两点D、E，连接DE，则四边形ABED的面积为 .

【解析】点A、B在反比例函数y=[8x]（x>0）的图像上，故可以设点A的坐标为（m，[8m]），根据点B为AC的中点，且点C在x轴上，所以点B的坐标为（2m，[4m]）.

又因为AD、BE与x轴平行，且点D、E在反比例函数y=[2x]（x>0）的图像上，易得点E的坐标为（[m2]，[4m]），点D的坐标为（[m4]，[8m]）.

∴S梯形ABED=[12]（BE+AD）h=[12]（2m-[m2]+m-[m4]）（[8m]-[4m]）=[92].

【点评】本题考查了反比例函数图像上点的坐标特征、直角坐标系中点坐标与线段长度的转化以及梯形的面积等，解题的关键是用参量m表示出点A、B、E、D的坐标.只要设出其中一个点的坐标，再用该点坐标所含的字母表示出其他点的坐标即可.

（作者单位：江苏省常州市武进区遥觀初级中学）