反比例函数中的典型错误与分析

王丽琴

反比例函数是同学们学习的一个难点，是在一次函数后又一个新型函数.一些同学由于对反比例函数概念理解不到位，对性质把握不准确，在解题过程中常会出现以下6种常见错误：

一、忽视对函数概念的理解

【例1】下列函数关系式中：y=[43x]，y=[2-πx]，y=[3x]+1，y=[-1x2]，y=-2x，5xy=3是反比例函数的有 .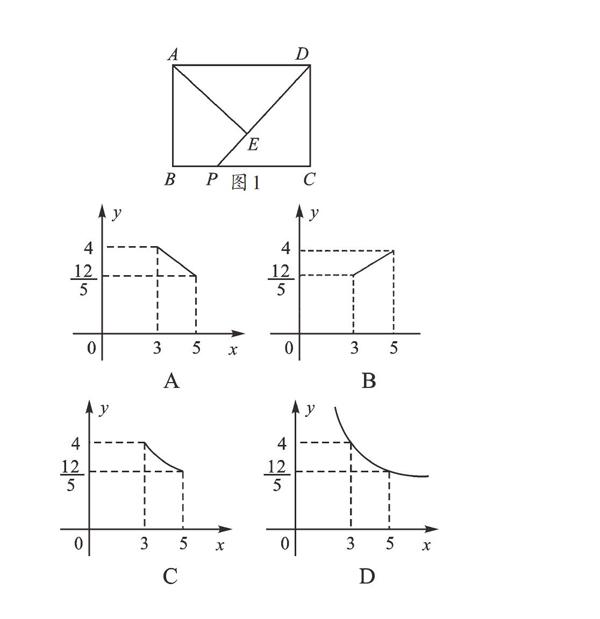

【错解】y=[43x]，y=[2-πx]，y=[3x]+1，y=[-1x2]，5xy=3或y=[43x]，y=[2-πx]，y=[3x]+1，5xy=3.

【错因】同学们会有以上两种错误答案，主要原因是对反比例函数概念理解不透.一般地，形如y=[kx]（k为常数，k≠0）的函数称为反比例函数.反比例函数通常有3种表达形式：y=[kx]，y=kx-1，xy=k.（上述3个式子中，k都为常数且k≠ 0）

【正解】y=[43x]，y=[2-πx]， 5xy=3.

二、忽视比例系数k≠0

【例2】若函数[y=m+1xm2+5m+3]是反比例函数，则m的值是 .

【错解】∵函数[y=m+1xm2+5m+3]是反比例函数，∴m2+5m+3=-1，解得m=-4或m=-1.

【错因】本题难度不大，主要考查同学们对反比例函数意义的理解.同学们要特别注意把反比例函数y=[kx]写成负整数指数的形式：y=kx-1时，自变量指数为-1，仍然有k≠0这个必要条件.

【正解】由题意得[m2+5m+3=-1，m+1≠0.]解得[m=-4或m=-1，m≠-1.]从而得m=-4.

k≠0是反比例函数定义的重要组成部分，同学们一定不能忽略.

三、忽视不同函数的k不同

求函数的解析式一般用待定系数法，先把已知条件中自变量与函数的对应值代入解析式得方程，再解方程求出待定系数，最后把待定系数的值代入所设解析式，得出解析式.

【例3】已知y=y1-y2，y1与3x成反比例，y2与x-2成正比例，并且当x=3时，y=5；当x=1时，y=-1.求y与x之间的函数解析式.

【错解】设y1=[k3x]，y2=k（x-2），k≠0.则y=y1-y2=[k3x]-k（x-2）.用待定系数法求解：当x=3时，y=5，代入得[k9-k3-2]=5，解得k=-[458].即y关于x的函数解析式为：y=-[158x+458]（x-2）.

【错因】此解法错在设函数解析式时，把y1与x，y2与x-2的比例系数设成相同的了，而实际上它们不一定相同，并且已知条件只代入了一部分.

【正解】设y1=[k13x]，y2=k2（x-2），k1、 k2≠0.则y=y1-y2=[k13x-]k2（x-2）.将x=3，y=5；x=1，y =-1代入得[k19-k2（3-2）=5，k13-k2（1-2）=-1，]解得[k1=9，k2=-4，]即y关于x的函数解析式为：y=[3x]+4（x-2）.

不同函数的k值是不同的.k只是一个字母，也可以用f表示.同学们要理解其真正的内涵.

四、忽视自变量的取值范围

【例4】如图1，在矩形ABCD中，AB=3，BC=4，点P在BC边上运动，连接DP，过点A作AE⊥DP，垂足为E，设DP=x，AE=y，则能反映y与x之间函数关系的大致图像是（ ）.

【错解】在矩形中连接AP，∵S△APD=[12]PD×AE=[12]AD×AB，∴xy=3×4=12，即y=[12x]，是反比例函数，故选D.

【错因】在判断函数的图像时，一定要注意自变量的取值范围.首先，当k>0时，反比例函数图像在第一、三象限；其次，同学们做题时已经考虑并知道了x>0，所以选了D，但是同学们忽视了自变量在实际问题中的取值范围.要使问题有意义，还要考虑P点是在BC边上运动的，所以y与x之间关系的图像是双曲线在第一象限图像中的一部分.

【正解】与上面一样，解得y=[12x]是反比例函数.∵当P与B重合时，AP=AB=3；当P与C重合时，AP=AC=5.∴不仅有自变量x>0，而且还有3≤x≤5，y与x之间关系的图像是双曲线在第一象限中的一部分，正确图像如C所示.

自变量的取值范围很重要，同学们一定不能忽视.

五、忽视性质成立的条件

对于反比例函数来说，当k>0时，图像分别位于第一、三象限，在同一个象限内，y随 x的增大而减小；当k<0时，图像分别位于第二、四象限，在同一个象限内，y随x的增大而增大.

【例5】已知P（x1，-2）、Q（x2，2）、R（x3，3）三点都在反比例函数y=[a2+1x]的图像上，则下列关系正确的是（ ）.

A.x1

C.x3

【错解】∵y=[a2+1x]是反比例函数，且k=a2+1>0，∴y随x的增大而减小.又∵-2<2<3，∴x3

【错因】当k>0时，反比例函数的图像在第一、三象限内，且在每一象限内，y随x的增大而减小，但点P（x1，-2）与Q（x2，2）、R（x3，3）不在同一象限内，因而不能由-2<2<3，就断定x3

【正解】∵k=a2+1>0，∴y随x的增大而减小，且函数图像分布在第一、三象限内.∵2<3，∴x3

本题考查了同学们对反比例函数图像的性质及其增减性的理解.在应用反比例函数图像性质的基础上，同学们应会正确地比较在不同象限内点的横、纵坐标值的大小关系.

六、忽视函数图像的变换

反比例函数的图像特点是：以原点为对称中心的中心对称的双曲线，反比例函数图像中每一象限的每一支曲线会无限接近 x轴、y轴，但不会与坐标轴相交（k≠0）.而一次函数图像是直线，所以结合两种图像的性质特征，可利用数形结合求一类不等式的解集.

【例6】如图2，直线y1=k1x+b与双曲线y2=[k2x]交于A、B两点，其横坐标分别为1和5，则不等式k1x<[k2x]+b的解集是 .

【错解】∵直线y1=k1x+b与双曲线y2=[k2x]交于A、B两点，又∵点A横坐标为1，点B横坐标为5，∴当y15.

【错因】要求不等式k1x<[k2x]+b的解集，不等式右边不是一个典型的反比例函数的形式，需要将其变换为一般形式.

【正解】∵由k1x<[k2x]+b，得到不等式k1x-b<[k2x]，∴令双曲线不动，直线y1=k1x+b向下平移2b个单位，得y=k1x-b，直线向下平移2b个单位后的图像如图3所示，交点A′的横坐标为

-1，交点B′的横坐标为-5，当-50时，双曲线图像在直线y=k1x-b图像上方，∴不等式k1x<[k2x]+b的解集是-50.

图像怎样做到平移呢？图像的平移综合成一点就是8个字：左加右减，上加下减.

总之，反比例函数的易错题因人而异，同学们可以根据自己的学习情况进行辨析，以便强化记忆，查漏补缺，总结经验，从而达到最好的学习状态.

（作者单位：江苏省常州市武進区星辰实验学校）