关于高速环道横断面设计探讨

顾 旻，钱 晨

（1.上海市政工程设计研究总院（集团）有限公司，上海市 200092；2.上海市政交通设计研究院有限公司，上海市 200030）

0 引言

在测试汽车处于极速、高速行驶情况下的稳定性、耐久性试验中，高速环道测试占有举足轻重的地位，各国政府机构和有实力的汽车制造商纷纷建设自己的高速环道。

由于高速环道的设计车速远超一般公路，其平曲线的类型和几何设计方法均不遵循现行规范的规定。目前世界上多数高速环道的缓和曲线类型为布劳斯（Bloss）曲线和麦克康奈尔（Mcconnell）曲线，经实践证明两者均是比较理想的。随着国内汽车工业的发展，高速环道的建设与使用案例逐年增多，关于两种曲线的介绍与探讨的文献也逐年增多，孙连举[1]、李运胜[2]、林本炎[3]等人均对高速环道的设计方法进行了研究，但多数讨论集中于平面线形设计，对高速环道横断面的设计方法探讨较少。本文重点讨论高速环道横断面的设计方法。

1 高环横断面的确定要素

笔者认为，高环横断面设计的第一步是确定平衡车速、车道规模和曲线形式这三个要素，三者相互联系，并且缺一不可。

1.1 平衡车速

平衡车速的确定取决于试验车辆的种类和性能。根据统计，世界各国使用中的汽车试验场高速环道最高平衡车速一般为120～250 km/h，其中最高平衡车速在180 km/h以下的高速环道大多修建于1960年以前。根据日本修建汽车试验场高速环道的经验,高速环道理想的设计车速一般为180~250 km/h；美国汽车工程师协会（SAE）则推荐新建汽车试验场高速环道的设计车速应控制在225~240 km/h之间[4]。近年来国内汽车试验场的最高平衡车速也均在200 km/h以上，其他车道的平衡车速则根据曲线类型和计算需要预先确定，一般分布在60~200 km/h之间，以满足不同车辆的试验需求。

1.2 车道规模

车道规模包括车道数和各车道的宽度。在确定平衡车速后，一般根据最高和最低平衡车速之间的差值即可确定车道数，相邻车道的速度差一般控制在60 km/h以下，若车速差过大，一方面会使横断面曲线曲率变化过快而给设计和施工带来困难，另一方面也会给车辆试验带来安全隐患。近年新建的高环高低平衡车速差约为140~180 km/h，4车道是比较合理的车道规模。

高速环道的车道宽度可以借鉴普通公路的计算方法[5]，以车辆后轮轴距、两车后轮外缘之间的安全距离和两车的车速来确定车道宽度，具体公式如下所示：

式中：S为后轮外缘与车道外侧之间的安全间隔，m；D为两汽车后轮外缘之间的间隙，m；M为后轮外缘与车道内侧之间的安全间隙，m；v1、v2分别为被超车与超车的车速，km/h。

图1 普通公路的车行道宽度计算

由于曲线的关系，两车之间的最小距离并非在后轮外缘，而是在车顶，且这一规律随着曲率增大和车辆高度增加而更加明显，因此在计算车道宽度时还应考虑由于曲率和车辆高度产生的车顶距离减小的因素。

如图2所示，曲线段车道间距需增加的宽度计算可简化为：

式中：Δ=为曲线段车道间距需增加的宽度，m；θ为相邻车道平衡状态下的倾角，°；h为车辆高度，m。

图2 曲线段两车最小距离示意

由于高速环道的平衡车速普遍高于120 km/h，公路车道宽度计算的经验公式并不能完全适用，笔者收集了国内外部分试车场的相关资料作为参考，详见表1。

通过表1我们不难看出，低速和中速车道的车速与普通高速公路接近，因此宽度取值≤4.0 m，次高速、高速车道的速度值较高，车道宽度范围介于4.0~4.5 m之间。

1.3 曲线形式

高速环道曲线段横断面的曲线形式通常采用高次抛物线或者复合高次曲线。关于曲线形式的选择，很多专家都做过分析。普遍认为，当采用高次抛物线时，三次抛物线的设计车速与横断面宽度呈线性增长，是比较理想的曲线形式，但设计时应进行双轮差的验算[1]；当采用复合高次曲线时，可以根据各车道的实验车型确定曲线组合，一般而言，货车道多采用一次或二次曲线以满足曲率半径的要求，轿车多采用三次曲线，但这种曲线将带来在车道变换处曲率不连续的问题。

2 横断面设计方法

本文重点探讨车道投影等宽技术和车道实际等宽技术这两种横断面设计方法，以三次抛物线设计为例：

其中，车道投影等宽技术是保持每根车道的水平投影宽度不变，即曲线超高段与直线段车道的水平投影宽度相等（与普通公路的设计方式相同），而车道的实际宽度则随着曲线坡度的增加而变宽；车道实际等宽是保持每根车道的实际宽度不变，车道的水平投影则随着缓和曲线向圆曲线过渡而逐渐变窄。

2.1 基本平衡方程

车辆在高速环道曲线段行驶的基本平衡状态如图3所示。在不考虑横向摩擦力的情况下，当重力的切向分力与离心力的切向分力相等时，车辆处于平衡状态，此时的行车速度则定义为该车道的平衡车速。实际试车时，横向摩擦力的存在为试车速度提供了一定的容错空间，但也会增加轮胎的磨损。受力平衡图见图3。

表1 国内外部分试车场设计车速和车道宽度指标

图3 曲线段车辆受力图

化简可得：

式中：m为试验车辆的质量，kg；g为重力加速度，m/s2；R 为行驶半径，m；v为试验车速，m/s；θ为该平衡位置状态下车辆的倾角,°。

2.2 车道投影等宽设计方法

以高环第一车道内边线为原点建立如图4所示的坐标系，根据车辆试验要求确定的低速、次高速（或中速）和高速车道的设计车速及车道设计宽度（车道水平投影宽度）可得方程组

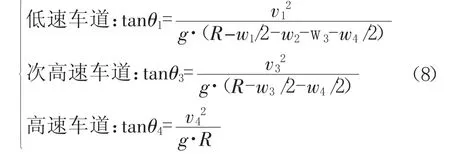
式中：v1、v2、v3、v4为 第 1、2、3、4 车道的设计车速，m/s；w1、w2、w3、w4为 第 1、2、3、4 车道的水平投影宽度，m。

图4 车道投影等宽计算方法示意图

其他参数意义同公式7。

对三次抛物线分别在各车道中心位置求导，可得方程组

式中：a、b、c为常数项；其他参数意义同公式8。联立上述两组方程组可得

将高速环道曲线段上任意一点的平曲线半径R带入上述三元一次方程组，可求出相对应点的a、b、c，加上由纵断面方程确定的常数d，即可得到整个高环曲线段任一点的三次抛物线方程。

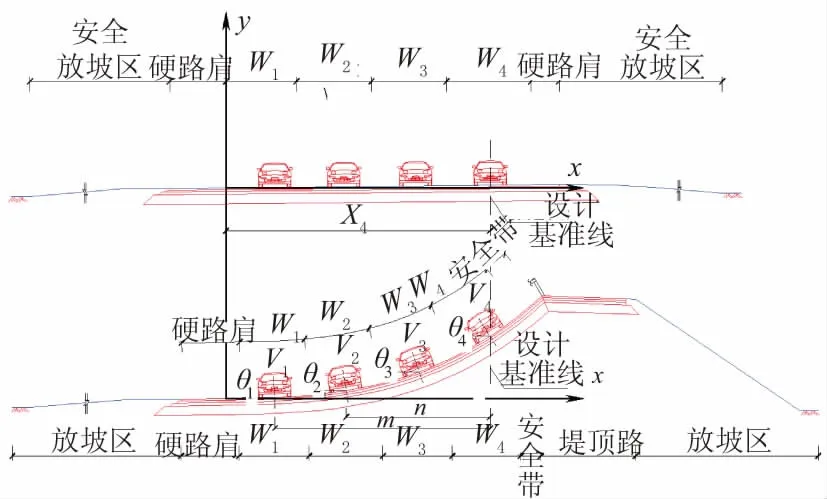
图5 车道实际等宽计算方法示意图

2.3 车道实际等宽设计法

以直线段第一车道边线为纵坐标零点建立直角坐标系，根据车辆试验要求确定的低速、中速、次高速和高速车道的车道设计宽度 w1、w2、w3、w4，则高速环道设计基准线（即第四车道中心线）的位置为l=w1+w2+w3+w4/2。假设坐标系和设计基准线的位置不变，仅曲线方程发生变化，同时为计算方便，引入未知数m表示圆曲线第一车道和第四车道中心线间的水平距离，应用弧微分公式：

则第一、四车道中心线之间的曲线距离可建立方程：

同理，引入未知数n表示圆曲线第二车道和第四车道中心线间的水平距离，则第二、四车道中心线之间的曲线距离可建立方程：

利用上文的平衡方程，可得方程组

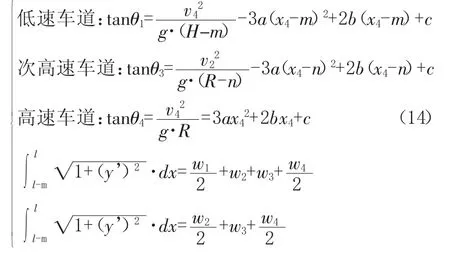
其他参数意义同公式8。

将高速环道曲线段上任意一点的平曲线半径R带入上述三元一次方程组，可求出相对应点的a、b、c、m、n，加上由纵断面方程确定的常数 d，即可得到整个高环曲线段任一点的三次抛物线方程。

3 两种设计方式的对比

目前两种设计方式在世界上应用均较为广泛，欧洲的OBERMEYER公司采用车道实际等宽技术，几乎包揽了欧洲的高速环道设计施工，日本的NIPPO公司采用车道投影等宽技术完成了日本多数高环的工程。两种技术所完成的高速环道在实际使用性能上并无明显的差别，但在设计施工过程中存在如下的不同之处：

第一是计算难度。车道实际等宽方法在设计时需要进行大量的的微积分运算，若不借助数值计算方法和计算机技术，很难完成运算。而车道投影等宽方法则能求得精确解，计算也不复杂。但在计算机高度发达的今天，这一差距已经可以忽略。

第二是土方工程量。车道投影等宽方法在设计时，曲线段的车道实际宽度会明显大于直线段，随之带来的是土方量的增加。且这一现象随着最高平衡车速的增加（曲率的增加）而越发明显。在合理的车道宽度下，曲线段加宽的车道所带来的容错率的增加对于专业试车员来说显得微乎其微，但增加的工程量却带来成本、工期等多方面的影响。

综上，笔者推荐采用车道实际等宽的设计方法。

4 结语

重点探讨高速环道横断面设计时如何确定三要素：平衡车速、车道规模、曲线形式，在此基础上介绍了车道投影等宽和车道实际等宽两种设计方法，并进行了定性的对比分析，得出以下结论：

（1）目前综合性试车场的高速环道的最高平衡车速不应小于200km/h，宜选择220~240 km/h。

（2）综合考虑使用需求和车速分布特点，高速环道车道数宜选用4车道。低速、中速车道的宽度可选3.5~3.75 m，次高速、高速车道的宽度宜选择4~4.5 m，车道外侧安全带的宽度可根据需求调整，一般在2 m宽度内。

（3）横断面曲线可采用高次抛物线或者复合曲线，当采用高次抛物线时宜采用三次抛物线。

（4）横断面设计推荐采用车道实际等宽的设计方法。相较车道投影等宽技术，车道实际等宽设计时能够减少工程土方量，从而减小工程总投资。