高大模板支撑系统数值模拟分析研究
王文洪 陈芝轩 刘宝林 白海珠
云南建投第五建设有限公司 云南 昆明 650106
近年来,随着社会的快速发展,土木工程高大模板支撑体系运用越来越多,支撑体系主要由立杆、横杆、支撑、连接件等构成;立杆是直接承担竖向荷载的构件,横杆的作用是减小竖杆的计算长度,支撑起到抵御水平荷载和增强结构整体性的作用,而连接件是各类杆件有效发挥作用的关键。支撑体系的立杆是典型的受压杆件,立杆最可能出现的破坏方式是压杆失稳,而非承载力极限破坏。
由于施工方案考虑不到位或实施过程中未按方案实施,导致支撑体系倒塌的事故时有发生。以某高速公路现浇箱梁模板支撑方案为例,该现浇箱梁高1.4 m、预应力现浇箱梁高2.0 m、现浇实心板厚0.7 m,支架搭设高度6.0~14.0 m。我们取现浇箱梁高1.4 m,搭设高度14.0 m,支架立杆纵距0.90 m,横距0.60 m,步距1.20 m,采用φ48 mm×3.25 mm碗扣式满堂支架模板支撑方案,建立与实际相符的三维结构模型,进行系统数值模拟分析研究,以进一步验证模板支撑方案[1-2]。
1 结构建模和计算
本次模拟采用空间有限元分析软件Midas Gen(版本号v836),杆件采用梁单元,Q235钢材,截面尺寸φ48 mm×3.0 mm,计算考虑剪切变形。按实际施工方案在模型中建立立杆、横杆、剪刀撑,对横杆考虑不同的节点转动刚度,支座条件为两向铰支。上部现浇箱梁按真实截面尺寸建立实体单元,程序自动计算自重,上部结构具有一定刚度,相比支撑体系的刚度大得多,可近似看作刚体,起到内力重分布的作用,通过上部实体单元可将恒荷载、活荷载以相对贴合实际的方式施加到支撑体系上(图1)。

图1 现浇箱梁模板支架示意(单位:cm)
分别对横杆节点转动刚度为0、4、12、20、40、60、80 kN·m/rad的7个半刚性节点(钢结构杆件间的连接是一种介于铰接和刚接的半刚性连接,节点的真实刚度不会是一个不变的特定数值)模型和1个刚性节点模型进行结构静力计算和屈曲分析。本文先以节点转动刚度40 kN·m/rad的模型为例分析结构的应力分布、变形特征和失稳形态。再将不同节点转动刚度的模型进行对比,分析节点刚度对结构受力和稳定性的影响。
2 应力、变形和稳定性分析
以横杆节点转动刚度为40 kN·m/rad的模型为例,对该模板支撑体系的应力分布、变形特征和失稳形态进行分析。
2.1 应力分布
分析在静力作用下的应力分布可以看出,结构绝大多数杆件应力在20 MPa以内,少数杆件的应力明显大出平均水平,相似位置相同类型的杆件应力基本相同,最大压应力55 MPa,最大拉应力46 MPa(图2)。
最大压应力出现在极少数的立杆上,达到55 MPa,具体位置为:受到上部现浇箱梁传导的竖向荷载,并将荷载直接向下传递到竖向支撑和下层立杆的顶层立杆。竖向荷载在此处由单根立杆承受,而向下一层传递时由竖向支撑和下层立杆3根杆件共同承受。由于竖向支撑的存在对局部刚度进行了强化,该节点在同等竖向荷载下的竖向变形小于周边节点,因此在上部结构具有一定刚度时,会产生内力重分布,变形较小处会产生更大的内力,故此类位置的单根立杆应力远超周边杆件。结构最大拉应力出现在水平支撑上,达到46 MPa。
立杆均受压应力,底层立杆的压应力大多为8~30 MPa,横杆既有压力也有拉应力,大多为0~2 MPa,水平支撑所在平面内的少数横杆达到7 MPa。结构竖向荷载基本都由立杆承担,在计算荷载下,应力远未达到极限应力,承载力尚有很大富余。大多数横杆主要起到约束立杆、减小计算高度的作用,受力很小,水平支撑所在平面内的横杆还起到一定的传力作用,但受力也不大。
普遍而言,立杆的应力由上往下,逐层增大,底层立杆应力多为8~30 MPa,顶层立杆应力多为4~20 MPa,与支撑相连的单根立杆应力往往比未与支撑相连的立杆应力要大。
因此,竖向支撑交汇于一个结点且仅有单根立杆与其直接传力的部位,是本结构应力控制的重点位置,此外,立杆、支撑的应力较横杆大。
2.2 变形特征
结构在静力作用下的变形整体均匀,以竖向变形为主,顶层位移最大,往下逐层减小。在竖向支撑处因竖向刚度得到斜杆的加强,位移量较未设支撑处要小(图3)。

图2 整体应力分布

图3 整体变形云图
2.3 失稳形态
由屈曲分析得到的第一阶屈曲模态(图4、图5)可知,结构首先是局部立杆受压失稳,而后达到临界值,导致整个结构失去稳定性,率先失稳的是未受到竖向剪刀撑约束的立杆。在竖向剪刀撑的平面内,一方面,剪刀撑承担了一部荷载,立杆承担的竖向荷载减小;另一方面,剪刀撑为立杆提供了额外的平面内约束,有效减小了立杆计算高度,从而局部保持稳定。

图4 结构一阶屈曲模态(侧视)
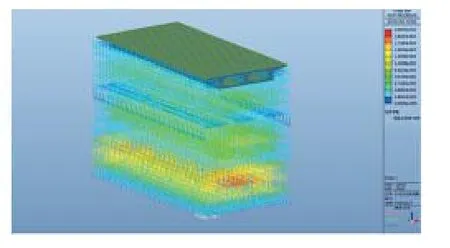
图5 结构一阶屈曲模态(斜视)
3 节点刚度的影响规律
分别取横杆节点转动刚度为0、4、12、20、40、60、80 kN·m/rad和节点完全刚接的模型进行分析计算,得出静力计算和屈曲分析结果,分析节点刚度对结构受力和稳定性的影响。虽然实际工程中的节点刚度因连接方式以及安装质量而无法准确定值,但本次计算取值的刚度范围包含了节点可能的刚度区间,得出的规律有一定借鉴意义。经对比分析,节点刚度变化对应力分布和变形特征无影响,但对变形最大值有影响,对结构的稳定性也有较大影响。
3.1 节点刚度对变形最大值的影响
从最大位移随节点转动刚度变化曲线(图6)可知,结构的最大位移随刚度增大而减小,刚度达到一定值后影响逐渐变小。
3.2 节点刚度对稳定性的影响
从结构稳定性随转动刚度变化曲线(图7)可知,结构的稳定性(即临界荷载系数)随刚度增大而增大,且影响程度随刚度增大逐渐变小。

图6 节点刚度-最大位移曲线
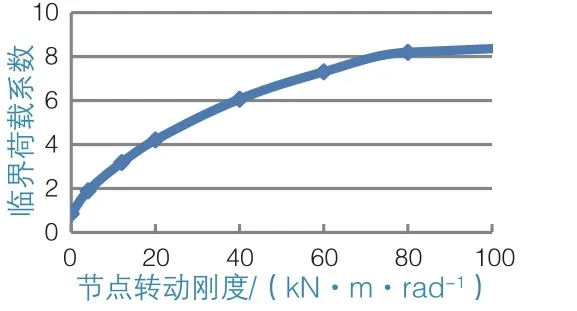
图7 节点刚度-临界荷载系数曲线
节点转动刚度不同时,结构失稳形态有所不同,取节点转动刚度0、40 kN·m/rad和节点刚接的模型进行对比,可以看出:
1)刚度为0 kN·m/rad时,结构失稳形态是部分立杆发生压杆失稳。中间层横杆和水平支撑对立杆几乎产生不了约束,立杆的失稳形状是一个半波正弦曲线,也可以认为立杆的计算长度较大,整体结构较容易失稳(图8)。
2)随着刚度增加,结构失稳形态是大多数立杆发生压杆失稳。中间层横杆和水平支撑对立杆产生明显的约束作用,立杆的失稳形状是多个半波正弦曲线,也可以认为立杆的计算长度较小,结构不易失稳(图9、图10)。
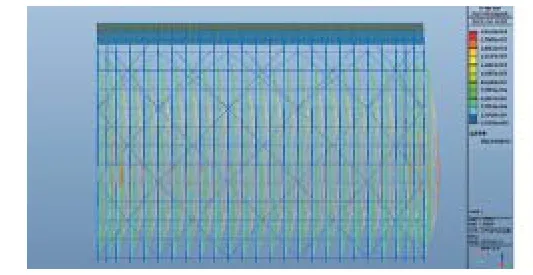
图8 转动刚度0 kN·m/rad时的一阶屈曲模态

图9 转动刚度40 kN·m/rad时 的一阶屈曲模态

图10 节点刚接时的一阶屈曲模态
由分析可知,刚度为0 kN·m/rad(即铰接)时,横杆和水平支撑的作用得不到有效发挥,立杆较易发生失稳,导致结构整体稳定性差。完全铰接为极端情况假定,在实际工程中并不存在,但也说明了节点保证一定刚度的重要性。而具有一定节点刚度的模型,中间层横杆和水平支撑对立杆产生明显的约束作用,立杆不易发生失稳,结构整体稳定性好。就本次建模的结构而言,节点转动刚度4 kN·m/rad及以上的模型均有较好稳定性。支撑架节点的实际转动刚度一般都能达到10 kN·m/rad以上,故本次针对的模板支撑体系失稳形态合理,结构整体稳定性较好[3-4]。
4 结语
模板支撑体系应力、变形的分布总体均匀,实际施工中应主要控制几个关键部位。竖向支撑交汇于一个结点且仅有单根立杆与其直接传力的部位、底层立杆是本结构应力控制的重点位置,该类结构应注意竖向支撑带来的支架变形不协调会造成内力重分布,可能导致局部立杆应力较大。该结构位移以竖向位移为主,无竖向剪刀撑的位置位移量较有竖向剪刀撑的位置大,顶层位移量较底层大,应重点观测。

