集装箱码头装船顺序和场桥行驶路径联合优化
郭文文,计明军,祝慧灵,王清斌
(大连海事大学 交通运输工程学院,大连116026)
0 引言
集装箱码头作为连接不同运输模式的枢纽节点,其作业效率的高低很大程度上取决于堆场的作业效率.在出口箱装船作业过程中,不合理的场桥行驶路径和装船顺序会导致堆场倒箱操作的产生,直接影响了堆场作业效率.因此,码头操作人员需要对装船顺序和场桥行驶路径联合优化,提高堆场作业效率.
倒箱操作是影响堆场作业效率的重要因素,众多学者研究了确定装船顺序下的堆场倒箱问题.Kim等[1-2]考虑了重量因素对出口箱存储位置的影响,建立了目标为最小期望倒箱量的数学模型.Lee等[3]利用邻域搜索启发式方法优化了堆场预翻箱方案.Zhu等[4]提出了更深层次迭代A*算法解决倒箱问题.周鹏飞等[5]建立了基于Petri网的翻箱模拟仿真模型及二次翻箱量估计模型.Ting等[6]提出了定向搜索算法解决堆场倒箱问题.此外,关于倒箱操作,多数专家从集装箱所在堆场栈和层的二维角度进行研究,比如Petering等[7]、Jin等[8-9]均研究了堆场单个贝位内栈和层对倒箱量的影响.而场桥作为堆场作业的主要机械设备,部分学者对场桥调度问题进行研究,但多在确定装船顺序下实现场桥作业成本最小或运行距离最短的路径优化,比如Vis等[10]研究了单个街区内两台场桥的调度问题.He等[11]建立了堆场调度问题的动态调度模型,设计混合算法对特定堆场算例进行有效求解.乐美龙等[12]、Gharehgozli等[13]在已知装船顺序的前提下研究了场桥调度问题.
综上所述,关于堆场内倒箱操作和场桥作业的成果,均在确定装船顺序下进行研究,并没有关注装船顺序和场桥行驶路径的相互制约.然而,装船顺序和场桥行驶路径相互影响且对倒箱操作影响较大,同时,集装箱多堆存于多个堆场贝位内.因此,本文从堆场的贝、栈、层三维角度对装船顺序及场桥行驶路径联合优化,对提高堆场作业效率具有重要的实际意义.
1 问题描述
出口箱作业过程中,场桥根据船舶配载图可确定多种装船顺序,如图1所示,船舶贝位同一层中相同图案代表的集装箱可以交换顺序完成装船.图2为堆场作业过程,定义待提集装箱为目标箱,在装船过程中,存在多种目标箱类型,有些目标箱位于堆场贝位某一栈的最高层,场桥可直接将箱提走,有些目标箱并未堆放在最高层,定义堆放于目标箱之上的箱为阻碍箱,则场桥需将阻碍箱移至同一贝位的其他栈,称之为倒箱;同时,如果目标箱与上一个提取箱位于同一贝位内,则场桥不必在贝位间移动,否则场桥发生移动.由图2可知,不同装船顺序的产生会导致不同目标箱的选择,进而影响场桥行驶路径,使得倒箱量及场桥作业时间不同,反之亦然,不同的场桥行驶路径可以产生不同的装船顺序.因此,装船顺序和场桥行驶路径相互影响,为提高码头作业效率,港口应对装船顺序和场桥行驶路径联合优化.
本文在已知船舶配载图和堆场堆存状态的前提下,研究出口箱装船过程中的装船顺序和场桥行驶路径问题,联合优化装船顺序及场桥行驶路径产生的倒箱量,将倒箱量用场桥作业时间衡量,建立以最短作业时间为目标的联合优化模型,并设计均衡倒箱量及场桥作业时间的启发式算法对其求解,寻求最短的作业时间从而提高堆场作业效率.

图1 码头俯视图Fig.1 Terminal planform

图2 堆场作业过程Fig.2 Yard operation
2 数学模型
2.1 模型假设
(1)集装箱堆存状态和船舶配载图已知;
(2)堆存贝位内只允许堆存相同尺寸的集装箱,倒箱仅发生在堆场同一贝位内;
(3)场桥在堆场中的作业是匀速的;
(4)集卡的数量相对充足,满足场桥的作业需求,不存在等待问题,即集卡不是制约性因素.
2.2 模型符号与决策变量


(2)过程变量.
(3)决策变量.


2.3 模型建立
根据目标箱位于堆场栈的位置,分为4类:目标箱上无阻碍箱、目标箱上存在1个阻碍箱、存在2个阻碍箱及3个阻碍箱.当目标箱上存在3个阻碍箱时,目标箱的提取会极大地增加场桥的作业时间及堆场倒箱量,因此,本文避免了这一类目标箱的提取,只考虑直提箱、存在1个阻碍箱及2个阻碍箱的3类目标箱的提取,分别计算其提取过程中的场桥作业时间.
当目标箱ks上无阻碍箱时,提箱过程如图3所示,场桥作业时间tks为


图3 直提箱提取过程Fig.3 Loading process without rehandles
当目标箱ks上存在1个阻碍箱is时,场桥将is翻倒至落箱位js上,提箱过程如图4所示,场桥作业时间为
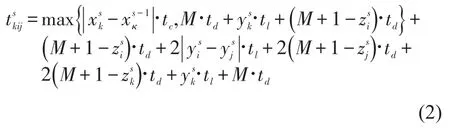
当目标箱ks上存在2个阻碍箱is和ps时,场桥先将ps翻倒至落箱位qs,将is翻倒至落箱位js,提箱过程如图5所示,场桥作业时间为

综上所述,本文建立以最短场桥总作业时间为目标的数学模型.

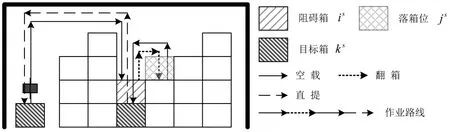
图4 存在1个阻碍箱的提箱过程Fig.4 Loading process with 1 rehandle
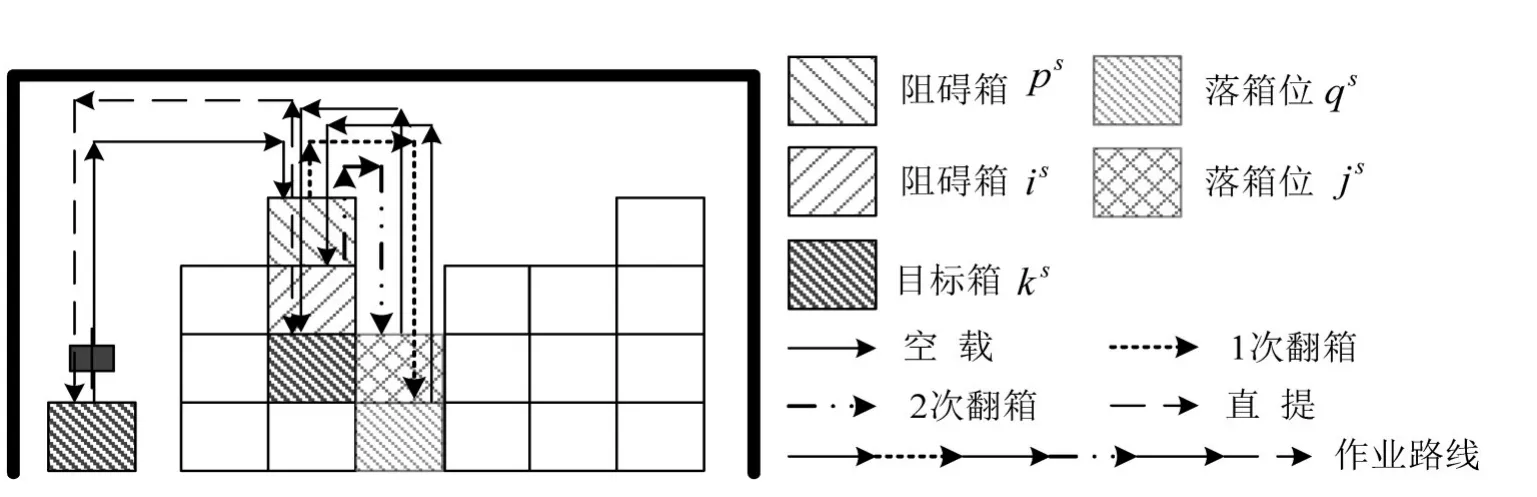
图5 存在2个阻碍箱的提箱过程Fig.5 Loading process with 2 rehandles
所有的目标箱都能被提取装船的约束为

场桥每次提取1个集装箱的约束为

集装箱在船舶上不能悬空放置的约束为
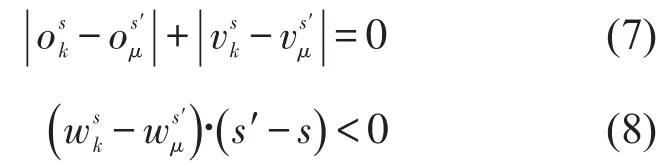
堆场贝位每一栈的堆存高度要小于最高可堆存高度的约束为

提箱装船和倒箱过程中目标箱所在的栈和落箱位所在栈的高度变化约束为
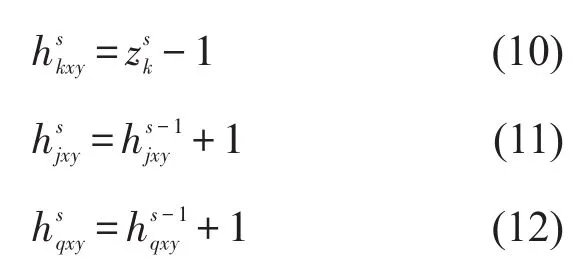
倒箱仅发生在同一贝位不同栈中,其约束为
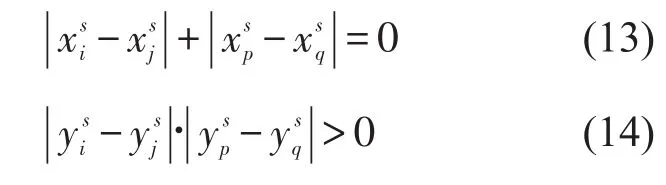
为了表示目标箱和阻碍箱位于堆场贝、栈、层之间的关系,其约束为

决策变量均为0-1变量,即

3 算法设计
3.1 算法原理
已知船舶配载图和堆场堆存状态,可确定多种装船顺序.假设集装箱的数量为N,则装船顺序的复杂度为N!,难以对问题进行求解.本文从船舶栈的最底层和堆场栈的最顶层进行研究,避免了集装箱在船舶上的翻倒,结合堆场堆存状态剔除部分不合理的可行解.在求解过程中,比较与前一目标箱位于相同堆场贝的箱及其他贝位直提箱的场桥作业时间,选择最短作业时间的箱作为目标箱,如果存在阻碍箱则将其翻倒至同一贝位的最矮栈中,直至所有目标箱完成装船作业.基于上述思想的均衡倒箱量及场桥作业时间的启发式算法,减少计算量,提高了计算效率.
3.2 算法步骤
基于上述算法原理,算法流程图如图6所示,具体步骤如下:
Step 1设定初始数据.确定集装箱数为N,场桥作业时间CT=0,倒箱量R=0,装船顺序集合LS.
Step 2确定初始装船集合S.根据船舶配载图,选择船舶贝位各栈最底层箱,构成集合S,确定S中箱所在堆场贝位栈的层数E及最高层数M,转Step 3.
Step 3判断是否存在直提箱.由S、E及M,计算L=M-E,判断L中是否存在元素0,即直提箱,如果存在,转Step 4;否则,转Step 5.
Step 4直接提取直提箱n.选择L中元素0中序号最小的箱作为目标箱,并确定场桥作业时间CT和所在堆场贝位bay,倒箱量R不变,转Step 8.
Step 5判断是否存在阻碍箱为1的箱.判断L中是否存在元素1,如果存在,转Step 6;否则,转Step 7.
Step 6提取阻碍箱为1的箱n1.选择L中元素1中序号最小的箱作为目标箱,确定场桥作业时间CT2、堆场贝位bay、倒箱量r,总场桥作业时间CT=CT+CT2,总倒箱量R=R+r,将箱n1记录到集合LS中,转Step 8.
Step 7提取S中最小序号的箱n1.选择S中序号最小的箱作为目标箱,确定场桥作业时间CT2、及堆场贝位bay、倒箱量r,总场桥作业时间CT=CT+CT2,总倒箱量R=R+r,将箱n1记录到集合LS中,转Step 8.
Step 8更新集合S、E及M,转Step 9.
Step 9判断S中是否存在位于bay堆场贝的集装箱n3.如果存在,转Step 10;否则,转Step 11.
Step 10确定提取n3所用的场桥作业时间CT3及倒箱量r,转Step 12.
Step 11判断是否存在直提箱n4.根据更新的集合S、E及M,计算L=M-E,判断L中是否存在元素0,如果存在,转Step 17;否则,转Step 18.
Step 12判断是否存在直提箱n4.根据更新的集合S、E及M,计算L=M-E,判断L中是否存在元素0,如果存在,转Step 13;否则,转Step 16.
Step 13确定提取n4所用的场桥作业时间CT4,转Step 14.
Step 14判断CT3是否大于CT4,如果是,转Step 15;否则,转Step 16.
Step 15将箱n4记录到集合LS中,计算总场桥作业时间CT=CT+CT4,倒箱量R不变,bay为箱n4所在的堆场贝位,转Step 19.
Step 16将箱n3记录到集合LS中,计算总场桥作业时间CT=CT+CT3,倒箱量R=R+r,bay为箱n3所在的堆场贝位,转Step 19.
Step 17确定提取n4所用的场桥作业时间CT4,转 Step 15.
Step 18确定S中最小序号的集装箱n3及倒箱量r,转 Step 16.
Step 19判断集合LS的集装箱量是否为N.如果是,转Step 20;否则,转Step 8.
Step 20输出提取N个集装箱所用的总场桥作业时间CT及倒箱量R.
4 算例比较与分析
4.1 算例求解
本文基于上述算法,以14个集装箱为例,图7(a)表示船舶配载状态,图7(b)表示位于堆场不同贝位的堆存状态.利用Matlab对启发式算法进行求解,得到装船顺序及场桥行驶路径,如图8和表1所示.
图8为装船过程中的堆场变化,可以看出只需翻倒阻碍箱8,倒箱量为1.表1为启发式算法下的装船顺序及场桥作业时间,可以看到最优的装船顺序为1-2-6-4-8-13-5-10-11-3-7-12-9-14,场桥作业时间CT=1 744s.
4.2 下界分析
为了验证模型的有效性,计算理论上的下界至关重要,分析可知,场桥作业时间包括直接提箱产生的场桥作业时间及倒箱操作产生的场桥作业时间,装船过程中倒箱操作是不可避免的,不同的装船顺序会产生不同的倒箱量,影响场桥作业时间.因此,为缩短场桥作业时间,必须减少倒箱量的产生,使其趋向于0,即所有的集装箱直接装船,得到最短场桥作业时间.因此,本文计算了所有集装箱直接提箱装船的场桥作业时间,以此作为下界,验证算例的准确性.
具体的下界求解过程如下所示:
(1)根据船舶配载图,选择船舶贝位各栈最底层的集装箱,构成初始装船集合S.
(2)提取S中集装箱号最小的箱n,并计算直接提取箱n的场桥作业时间.更新S.
(3)直接提取与箱n同一贝位的集装箱,计算场桥作业时间,如果不存在同一贝位的箱,则继续提取集合S中箱号最小的,直至所有箱装船.

图6 算法流程图Fig.6 Algorithm flow chart
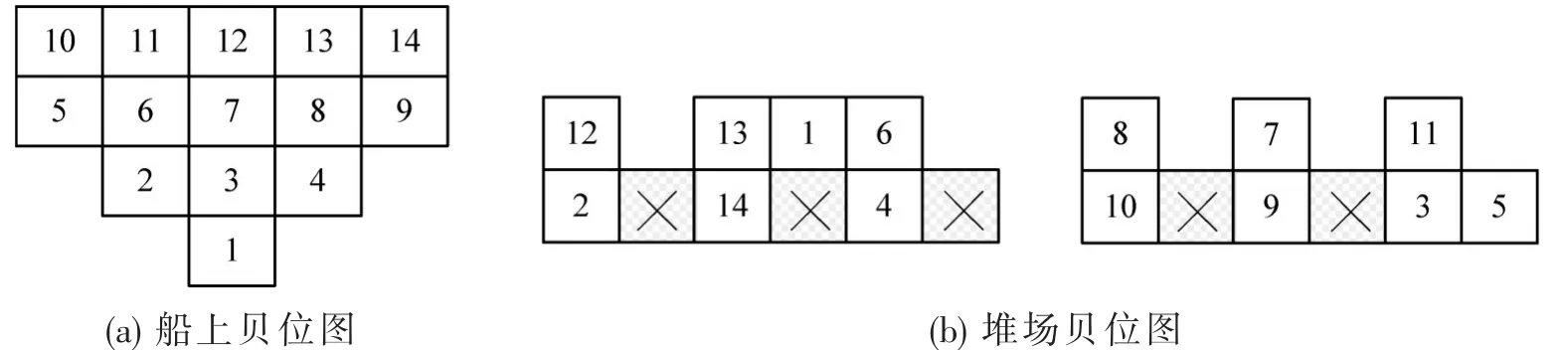
图7 船舶及堆场堆存状态Fig.7 Stacking status for ship and yard

图8 堆场状态变化过程Fig.8 Changing process of yard state
(4)将所有箱直接提取装船所需要的场桥作业时间作为该模型的下界LB,下界求解公式为
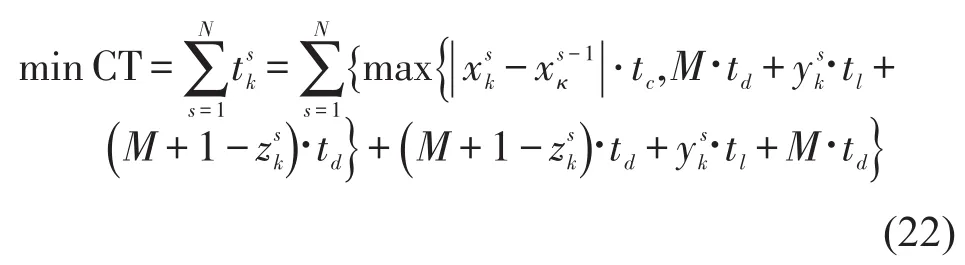
4.3 算法比较
本文利用Matlab编程语言开发,所得结果是在Intel Core 2 Duo3GHzCPU及2G内存平台下测得.为验证算法的可行性及通用性,本文对B×S×T(即堆场贝数×栈数×最高层数)的不同组合,随机生成集装箱规模为N的不同算例,针对不同规模的算例,采用了启发式算法求解,并进行对比分析,结果如表2和图9所示.

表1 装船顺序及场桥作业时间Table 1 Loading sequence and yard crane operation time
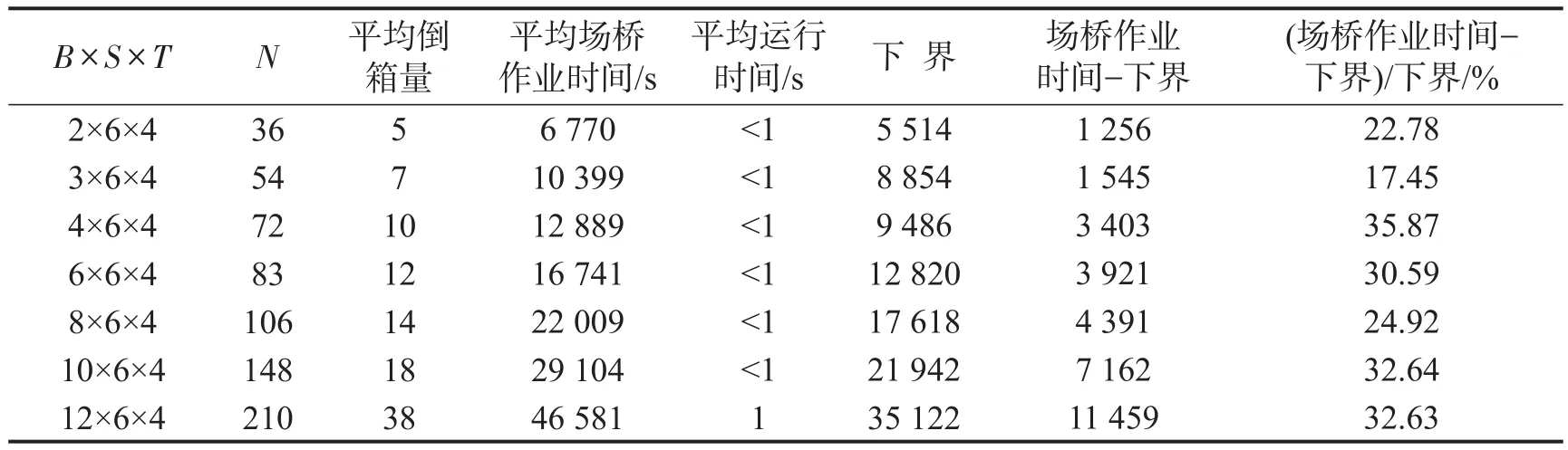
表2 启发式算法和下界比较Table 2 Comparison for heuristic algorithm and lower bound
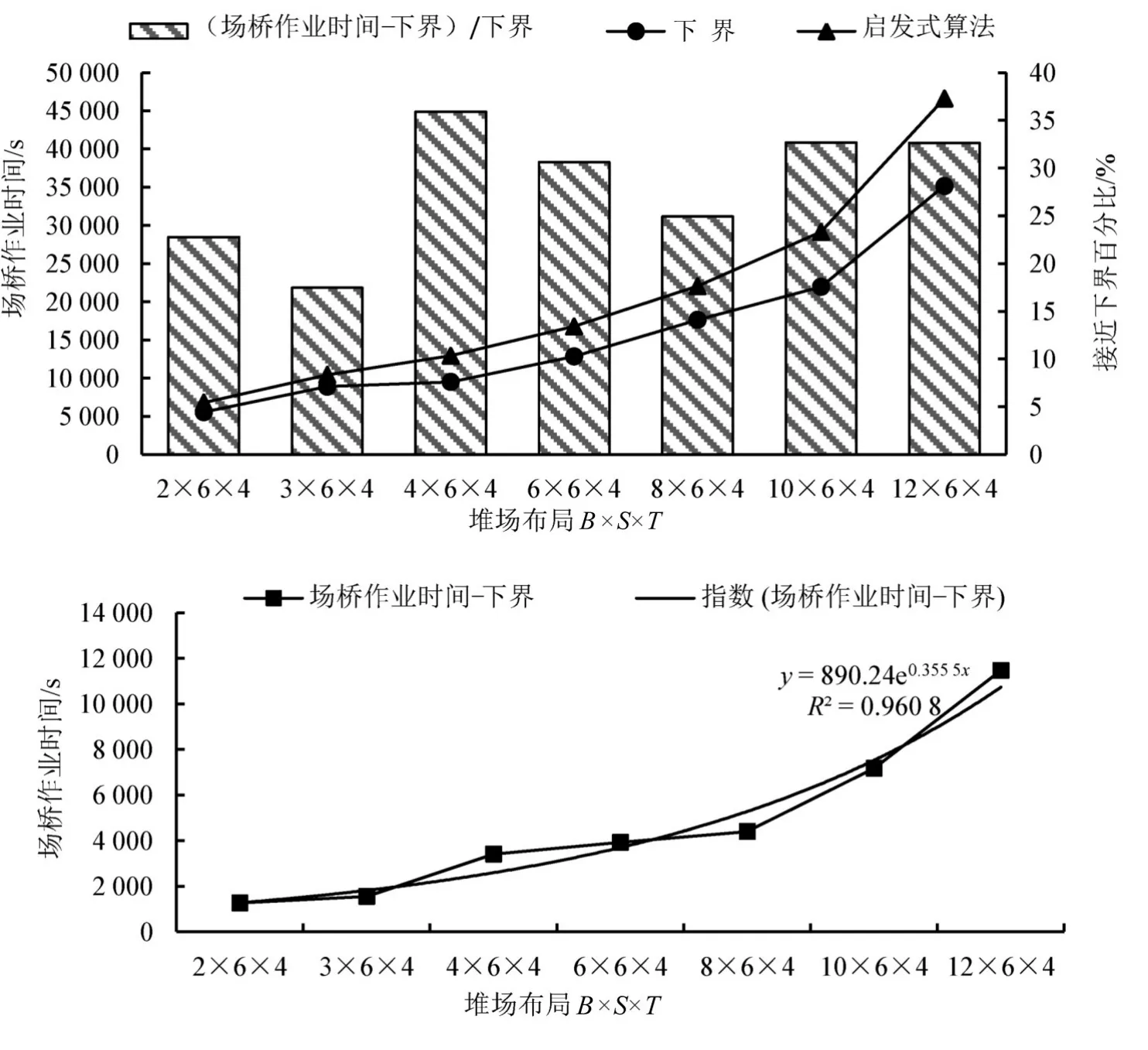
图9 算法分析图Fig.9 Algorithm analysis diagram
表2表示了启发式算法下不同规模算例产生的倒箱量、场桥作业时间及算法下界,得到以下结论:
(1)本文提出的启发式算法适用于不同规模下的集装箱作业,且随着集装箱规模的增大,场桥作业时间增加,算法运行时间变长,但仍较快获得计算结果,表明本文设计的模型及算法是有效的.
(2)装船顺序及场桥行驶路径联合优化下的场桥作业时间与下界相比,场桥作业时间的增加程度约为20%~35%,这主要是由于装船顺序及场桥行驶路径的不同导致不同倒箱量的产生,表明倒箱量对场桥作业效率影响较大.因此,码头操作人员可对装船顺序及场桥行驶路径联合优化,提高堆场作业效率.
(3)场桥作业时间与下界差值呈指数增长趋势,拟合曲线的可决系数为0.960 8,表明倒箱量对场桥作业时间影响较大.因此,码头操作人员应着重于降低倒箱量,降低场桥作业时间.
5 结论
集装箱码头堆场运作优化的重要目标之一是提高堆场作业效率.本文在已知船舶配载图及堆场堆存状态的前提下,研究出口箱装船顺序及场桥行驶路径联合优化问题,以作业时间衡量装船顺序产生的倒箱量及场桥行驶路径,建立了以最短场桥作业时间为目标的数学模型,设计启发式算法对模型进行求解,分析了该联合优化问题的下界,并通过算例实验对问题进行讨论.算例结果表明该联合优化问题在启发式算法下的场桥作业时间与下界相比增加的程度约为20%~35%,且场桥作业时间与下界差值呈指数增长趋势,同时,随着集装箱规模的增加,算法仍能较快得到最优解,验证了算法和模型的有效性和合理性,为码头调度人员提供了理论上的依据.

