带有最优流量记忆时间差的一类新格子模型

翟 聪，刘伟铭，黄 玲

(1.佛山科学技术学院交通与土木建筑学院，广东佛山528000；2.华南理工大学土木与交通学院，广州510640)

0 引言

近年来，随着交通保有量的日益增多，交通拥挤现象愈发严重，如何有效的缓解交通拥堵问题已经吸引了很多学者研究.基于研究方法的不同很多交通模型[1-8]被给出，如跟驰模型、元胞自动机模型、水动力模型等.1998年，日本学者Natagani从宏观模型出发首次提出了格子流体动力学模型[9]，该模型一经提出，日益成为了研究的重点，很多学者基于上述的格子模型进行改进，很多改进的新格子模型被给出，如2012年，G.H.Peng等基于考虑驾驶员的预测时间，提出了一类考虑有预测效应的新格子模型[10]，通过随后的理论分析和仿真算例验证了预测时间能够有效的缓解交通拥堵，提升交通流的稳定性；基于考虑流量差信息的最优估计，Shu-hong Yang等对原有的格子模型进行了改进[11]，同时验证了模型的新增项对于缓解交通拥堵确实是有效的；Tian C.提出了一类带有连续格点最优流量差信息的新格子流体动力学模型，同时还验证了考虑连续格点最优流量差信息能够有效地缓解交通拥堵[12]；为了分析连续格点之间密度差对交通流稳定性的影响，Jun-fang Tian基于以往的分析提出了一类新的格子流体动力学模型[13]；Hong-Xia Ge[13]为了增强文献[9]中所提出的的格子流体动力学模型的稳定性，从控制论方法出发，设计了一类新的滞后反馈控制器；为了分析连续格点的密度差信息对交通流稳定性的影响，Junfang Tian[14]提出了一类新的格子流体动力学模型，同时还验证了考虑密度差信息对于缓解交通拥挤是有效的.而其余关于格点模型的相关研究还可参阅文献[15-18].

从上述的分析我们可知，近年来，关于格子流体动力学模型的研究已经分析的较全面，然而以往的分析中仍然存在着一些局限性，如文献[19]中虽然分析了最优流量对交通流的影响，但是上述的论述中主要基于前后车的最优流量差的影响，一般的，在现实情形下，最优流量信息可以看成是驾驶员基于在当前道路状况所估计得到的最优速度，而驾驶员基于所“估计”得到的道路最优速度与车辆的当前速度的差值来对车辆的加速度进行调控，在上述的分析中并没有考虑到驾驶员记忆时间的影响；而文献[20]中指出驾驶员在行车过程中受到记忆时间的制约.为此，本文在传统的格子模型基础上，引入最优流量差信息，提出了一类新的格子流体动力学模型；基于线性稳定性分析和非线性分析方法，获得了新模型的稳定性条件和关于该模型的mKdV方程，通过求解该mKdV方程所得到的扭结—反扭结孤立波可用于临界密度附近交通拥堵的传播过程；最后，通过仿真算例验证了上述理论分析所得到主要结论的正确性.

1 模型的构建

1998年，日本学者Nagatani[9]首次提出了格子流体动力学模型，该模型可表示为

式中：ρ0表示平均密度；ρj,vj分别表示格点j在t时刻的瞬时密度和瞬时速度；a表示驾驶员的灵敏度值；表示最优速度函数，由变量ρj+1唯一决定，其表达式为

式中：ρc表示安全密度；vmax表示道路上的最大行驶速度.

式(1)表示连续方程，式(2)表示演化方程.然而该格子模型[10-20]中，并没有考虑驾驶员受记忆时间的约束，而文献[3]中提出：驾驶员的记忆时间在交通流的研究中是不可忽视的，当驾驶员感应到当前道路上最优流量信息时，往往会通过分析在记忆时间范围内该最优流量信息的变化幅度来调整下一步长下车辆的加速度值.为了更加全面的分析上述问题，本文在式(2)中新增记忆最优流量差，提出了一类新的演化方程，即

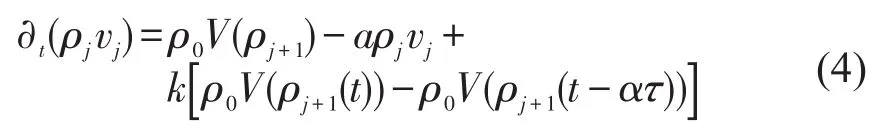
式中：α表示记忆时间步长的权重；k表示新增项(记忆最优流量差ρ0V(ρj+1)-ρ0V(ρj+1(t-ατ)))的权重.当α=0时，式(4)可转化为式(2).

为了简化分析步骤，我们对变量ρj+1(t-ατ)进行泰勒展开，同时忽略其中的非线性项，可得

因此，变量V(ρj+1(t-ατ))可转化为

式中：V'(ρj+1)=dV(ρj+1)/dρj+1.

将式(6)带入式(4)，同时综合式(1)，消除式(4)中的速度变量v，可得到

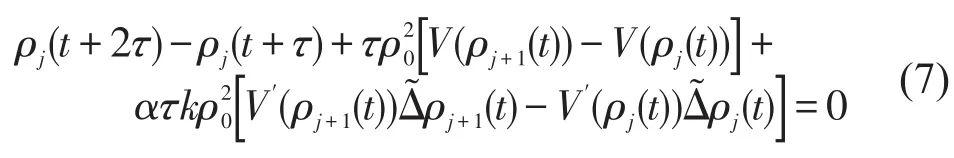
2 线性稳定性分析

为了分析记忆最优流量差对交通流拥挤演化的影响，对新提出的格子流体动力学模型进行线性稳定性分析.假设在均匀交通流情形下，统一将交通状态赋予恒定密度ρ0和最优速度V(ρ0)，该均匀交通流的稳定性状态解可等式为

假定yj(t)为关于格点j上稳定状态密度的一个微小的扰动，则

将带有扰动密度分析的式(9)带入式(6)，同时对该式进行线性化表示，可得

设定yj(t)=exp(ikj+zt)，将其带入式(10)，可得

将z=z1(ik)+z2(ik)2+…带入式(11)，可分别得到关于ik的一阶和二阶项((ik)2)的系数，即

基于控制论方法可知，当z2＜0时，该均匀稳态流将演化成非稳定的；相反，当z2＞0时，该均匀稳态流是稳定的，因此该均匀交通流的中性稳定性曲线可表示为

其中，该均匀交通流的非稳定性条件可表示为

当k=0.0或α=0.0时，上述的非稳定性条件与Nagatani’s格子模型[9]所给出的非稳定性条件一致，为此本文所提出的条件可以视为上述模型的一般化形式.

3 非线性稳定性分析

本文利用还原摄动方法分析了记忆最优流量差对临界点(ρc,ac)附近交通拥挤的传播演化问题进行了分析，基于参数ε(0＜ε≤1)，将时间慢变量T和空间慢变量X定义为

式中：b表示的是待定常数.

同时我们假定变量ρj满足

基于式(14)和式(15)，将式(7)展开至关于ε的5阶项，则我们可得到非线性等式

式中：系数ki可由表1获得，i=1,2,…,7；；在 临 界 点(ρc,ac)附近，我们有

为了消除式(16)中关于ε的2阶和3阶项，假定b=-ρ2cV'，则式(16)可转化为

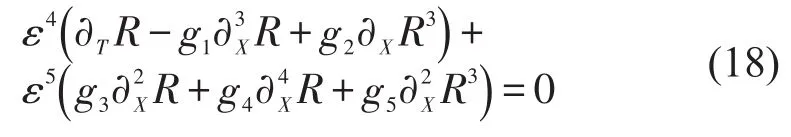
式中：gi可由表2给出，i=1,2,…,5.

为了将式(18)转化为标准的mKdV方程，引入式(19)的变换.

因此，式(18)可重新表示为

忽视式(20)中的校验项O(ε)，则可得到标准的mKdV方程，通过求解该mKdV方程，可得到扭结—反扭结孤立波为

式中：c表示扭结—反扭结孤立波的传播速度.同时为了确定该扭结—反扭结波的传播速度，则一定满足式(20)必要条件.

基于求解式(22)，可得到关于c的确定值为

则扭结—反扭结孤立波的解可表示为

则关于该孤立波的震荡幅度A为

表1 模型中关于ki的系数Table 1 The coefficient ofkiin the model

表2 模型中关于gi的系数Table 2 The coefficient ofgiin the model

基于上述mKDV求解所得到的扭矩反扭矩解代表的是共存相，在该相中兼具有低密度区下自由流相和高密度区下的阻塞相两部分，其中自由流相的密度表示为ρj=ρc+A，而阻塞相的密度表示为ρj=ρc-A，由自由流相密度和阻塞流相密度组成的曲线称为共存曲线，如图1所示.图1在(ρ,a)空间给出了共存曲线和中性稳定曲线，其中实线表示中性稳定性曲线，虚线表示共存曲线.整个相空间被两条曲线切分成3部分：稳定性区域、亚稳定区域和非稳定性区域.

图1(a)中，当α=0.0时，即模型中记忆时间为0，此时的带有记忆最优流量差效应的格子模型即为Natagani提出的格子模型；当存在记忆时间(α=0.3＞0.0)时，中性稳定曲线与共存曲线相比于Natagani格子流体动力学模型整体存在一定的下移，且临界值(ρc,ac)也有一定降低，说明增大了模型稳定区域的面积，使得交通流更容易达到稳定状态，从而可知，新的格子流体动力学模型与传统的Natagani的流体动力学模型的稳定性更强；而当记忆时间α继续增大时，该组曲线的纵坐标值(临界敏感系数)得以进一步的减小，稳定区域较Natagani所提出的格子模型时更加广泛，也即说明了记忆时间的时间步长对于增强交通流的稳定性是有效的.图1(b)分析了中性稳定曲线和共存区域在不同参数k下的变化情况，随着灵敏度参数k的增大，交通流的稳定区域逐渐增大，这也说明了权重系数k对于缓解交通拥挤是有效的.

图1 关于不同参数下(ρ,a)空间的相图情况Fig.1 The phase diagram in parameter space(ρ,a)

4 仿真算例

通过一些仿真算例验证上述分析的主要结论.首先，在周期有界条件下，我们将单向道路切分为N个格子，其中每个格点的初始密度可分别表示为

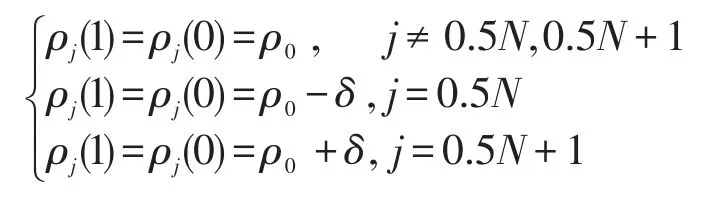
式中：δ表示初始干扰，δ=0.1；驾驶员的灵敏度a=1/τ=2.7；各格点的初始密度ρc=ρ0=0.25；格点总数N=100.

情形1参数k的影响.

图2为104s之后，在不同系数k下的密度波时空演变图.当k=0.1,0.2,0.3时，由于交通流模型均不满足线性稳定性条件式(11)，所以这3种交通流模型是不稳定的，当均匀流中存在干扰时，即使再小的干扰所造成的密度震荡幅度都会随着时间的演化而逐渐放大，最终变成阻塞波.图2(a)～图2(c)中出现扭结—反扭结孤立密度波，其中该扭结波的波动幅度随着敏感参数k的增大而逐渐降低，该结论与前面线性和非线性分析所得到的结论是相符的；图2(d)中，初始干扰所引起的密度震荡幅度随着时间的推演逐渐降低，最终消失近似形成自由波，在此情形下不易发生交通拥挤问题.对此，说明考虑记忆最优流量差确实是能够提高交通流的稳定性的.

图3为t=10 300 s时的瞬时密度分布情况.从图3可知：k=0.1,0.2,0.3所描述的并不是平稳状态的均匀交通流，然而该密度波的震荡幅度随着灵敏度k的增大而逐渐降低；相比于k=0.1的密度震荡幅度，k=0.4情形下的幅度值得到了有效的降低，此时交通拥堵近似消失.通过该现象可进一步表明系数k所代表的记忆最优流量差项的确能够抑制交通流的阻塞，减少交通流的震荡时间，提高交通流的稳定性，且当该灵敏度超过一定阈值时，即当仿真过程中给定的敏感系数满足稳定性式(11)时，均匀交通流系统中的小干扰能够被系统自身所稀释而抑制，图3中k=0.4情形很好的诠释了该类现象.因此，证明了：缓解交通流拥堵问题时考虑记忆最优流量差确实是有必要的.

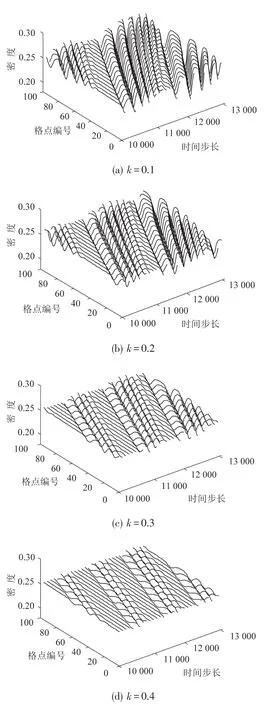
图2 在104步长后，不同的参数k下密度波随时间的演化情况(a=2.7,α=0.1)Fig.2 Space-time evolution of the density after104time step(a=2.7,α=0.1)

图3 图2中各子图在t=10 300时瞬时密度分布情况Fig.3 Density profiles of the density wave att=10 300 correspond to panels in Fig.2 respectively

情形2参数α的影响.

图4为在不同记忆时间步长α下所有车辆的密度—时间演化图像，其中，a=2.7,k=0.3.当α=0.0时，该模型与Natagani模型一致；当α=0.3时，满足交通流的稳定性；当α=0.0,0.1,0.2时，均不满足稳定性条件.图4(a)～图4(c)的3幅图中存在扭结—反扭结解，而图4(d)中未发现扭结—反扭结解，验证了本文中非线性分析的结论.图5是图4在t=10 300时所有车辆的瞬时密度情况，通过对比图5中4条曲线可知：车辆的密度震荡幅度随着α的增大而逐渐减小，即说明了记忆时间步长能够有效的增强交通流的稳定性；图中α=0.1,0.2,0.3时，曲线的振幅均大于α=0.0.α=0.0，也即Natagani模型，从而可知，考虑有最优速度在记忆时间变化项的新模型(a＞0.0)的稳定性要强于Natagani所提出的流体动力学模型.所以，增大驾驶员对最优流量随记忆时长变化的灵敏度系数k和记忆时间步长α都能够有效的影响交通流的稳定.

5 结论

基于分析记忆最优流量差对交通拥堵的影响，一类关于Nagatani’s格子模型的扩展格子模型被给出，通过线性稳定性分析，给出了新模型的稳定性准则，通过相图发现随着权重参数k和记忆时间步长α的不断增大，该模型的稳定性区域也逐渐增大，也即说明了参数k和α对于抑制交通拥堵是有效的；随后，在非线性分析部分通过求解mKdV方程所获得的扭结—反扭结孤立波描述了在临界点附近交通拥挤的相变特性，仿真算例结果验证了上述理论分析所得到的结论，从而证明了权重参数k和记忆时间步长α对于抑制交通拥堵是存在积极影响的.

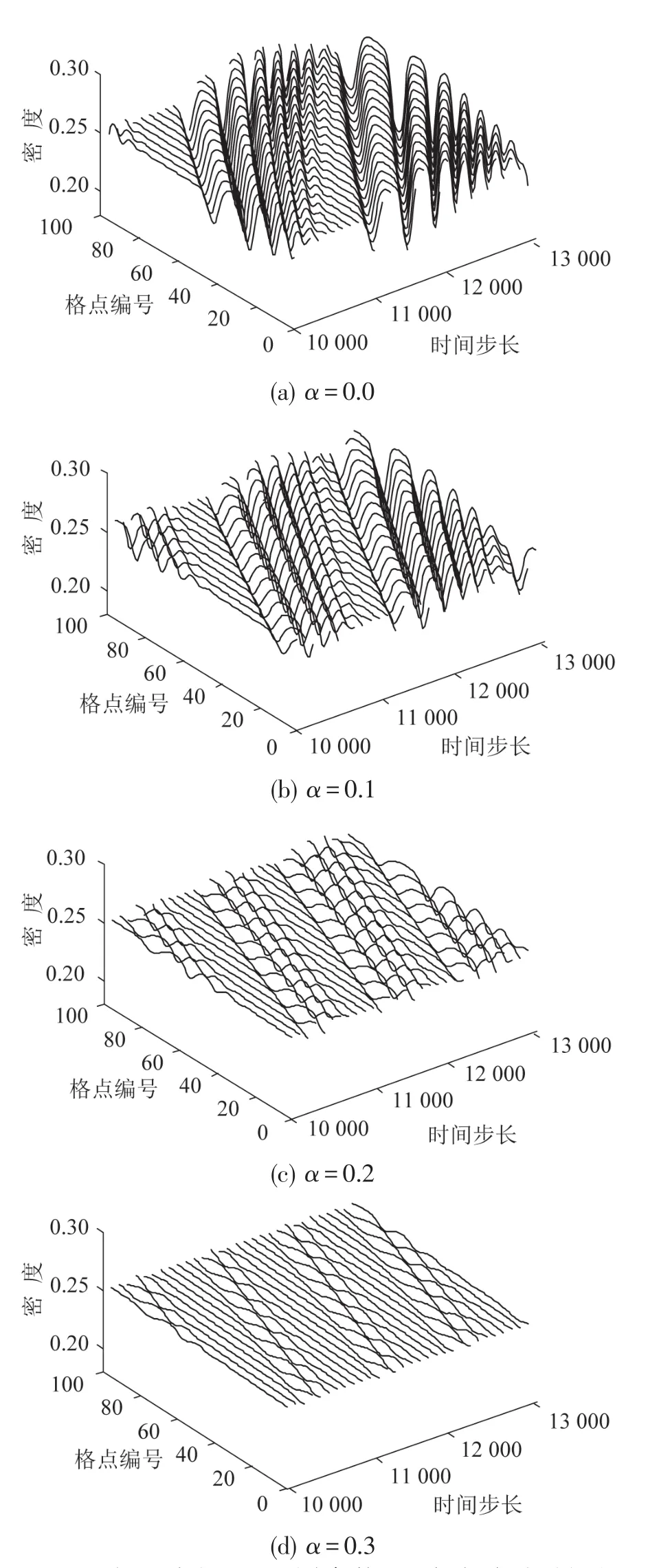
图4 在104步长后，不同参数α下密度波随时间的演化情况(a=2.7,k=0.3)Fig.4 Space-time evolution of the density after104time step(a=2.7,k=0.3)

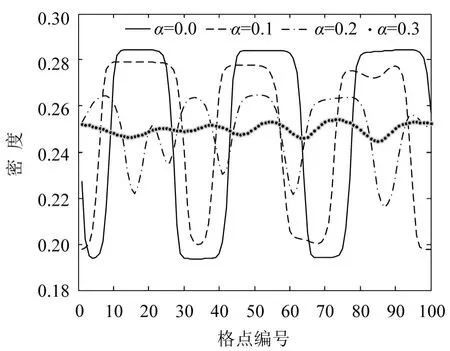
图5 图4中各子图在t=10 300时瞬时密度分布情况Fig.5 Density profiles of the density wave att=10 300 correspond to panels in Fig.4 respectively

尽管我们分析了记忆最优流量差对交通流稳定性的影响，然而，本文的研究主要局限于单车道情形，并没有考虑到实际环境下车辆的换道及超车行为，同时我们的研究主要基于仿真算例去分析，并没有利用实测数据进行校验，为此，我们在后续的研究中将对上述问题进行进一步的研究.