快递企业配送网络的鲁棒性及其提升对策研究
张 锦,秦 东
快递企业配送网络的鲁棒性及其提升对策研究
张 锦1,2,秦 东1
(1. 西南交通大学,交通运输与物流学院,成都 610031;2. 西南交通大学,综合交通运输智能化国家地方联合工程实验室,成都 610031)
为运用定量的方法提升快递企业配送网络的鲁棒性, 以某快递企业的订单号为数据来源, 通过网络爬虫、数据清洗等大数据处理手段, 获得其在全国范围内的配送网点与路径数据, 描绘了其配送网络的拓扑结构; 构建重要度评价矩阵确定了配送网络中重要节点, 并以其作为测试指标对该配送网络进行鲁棒性分析, 结果表明该配送网络对随机性破坏表现出鲁棒性, 对蓄意性破坏表现出脆弱性; 以投入成本为约束, 构造了鲁棒性优化模型, 运用Python求解, 验证了模型的可行性和有效性, 并以求解结果为依据, 对该配送网络提出鲁棒性提升对策。
配送网络; 复杂网络理论; 鲁棒性; 重要度评价矩阵; 鲁棒性优化模型
0 引 言
配送网络作为物流企业的核心,其布局的合理与否、性能的稳定与否将对物流企业的运转效率、运营成本、服务质量等起着决定性作用。因此,研究如何构建优性能、低成本、高效率的配送网络有着重要的意义。
目前,国内外学者主要运用线性规划、非线性规划等运筹学理论[1-4]和变分不等式等超网络理论[5-8]对配送网络的网点选址、车辆路径规划与优化问题进行研究,其主要的研究目的是不断完善最优化目标,选择、优化各类求解算法。由于复杂网络的复杂结构特征研究对分析复杂网络的拓扑结构、理解复杂网络的功能、发现复杂网络中的隐藏规律以及预测复杂网络的行为、提高复杂网络的鲁棒性不仅具有十分重要的理论意义,而且具有广泛的应用前景,因此它被广泛地运用于互联网[9]、通信[10]、医药[11]、商业[12]以及物流业[13-18]等众多领域。其中在物流业中的运用主要集中在对配送网络复杂结构特征、演化机理以及鲁棒性的研究[13-18]。谢逢洁等以陆运配送网络和航空配送网络为研究对象,分析了两类网络的复杂结构特性和演化机理,发现两类网络均属于小世界网络,但陆运快递网络的度分布有无标度特征、存在明显的社区结构,而航空快递网络的度分布有单标度特征、不存在明显的社区结构[13-15]。黄建华对公路配送网络进行了复杂结构特性和鲁棒性分析,结果表明,公路配送网络具有小世界和无标度特性,其遭受随机性攻击时表现出鲁棒性、遭受蓄意性攻击时表现出脆弱性[17]。杨华等研究了配送网络的统计性质和社团结构,发现配送网络具有小世界和无标度特性,且存在明显的社团结构[18]。但是,已有研究均只对配送网络面对随机和蓄意攻击时的鲁棒性进行了判定,并未对如何运用定量的方法提升配送网络的鲁棒性进行研究。因此,对其进行研究具有重要的理论和实践价值。
本文描绘了国内某快递企业配送网络的网络拓扑结构;然后构建重要度评价矩阵,确定配送网络中重要节点,并以其作为鲁棒性测试指标对该配送网络进行鲁棒性分析;最后构造了鲁棒性优化模型,运用Python求解,验证模型的可行性和有效性,以求解结果为依据对该配送网络提出鲁棒性提升对策。
1 配送网络的空间结构
本文以国内某民营快递企业2016年10月1日至2016年10月31日的78 986条订单数据为基础,通过网络爬虫得到该企业在全国范围内的399 739条配送路径,再经过数据清洗和数据整理,得到该企业在全国范围内的物流节点(转运中心/集散仓)分布以及物流节点之间的连通情况。运用Python 2.7和Gephi 0.8.1构造出该快递企业配送网络拓扑结构,如图1所示。

图1 国内某快递企业配送网络拓扑结构
图1中包括196个节点和399条边,1个节点代表1个物流节点所在城市,1条边代表两个城市之间的配送路线。图中节点形状大小与各节点的度值呈正相关关系,即节点的形状越大,该节点的度值越大。
关于图1中的数据,需要做以下几点说明:(1)不区分城市间的运输方式,即不区分城市间是通过何种运输方式进行配送,仅考虑城市之间是否存在配送路线,存在则连通,不存在则不连通。(2)不考虑城市间的配送量,即不考虑边的连接权重问题,将配送网络抽象为非加权网络;(3)不考虑配送方向,假设能从节点A到节点B,则默认为节点B也能沿相同路径到节点A,即将配送网络抽象为无向网络;(4)不考虑城市间配送的时间和成本等因素,也不考虑企业的经营管理能力等因素。
2 配送网络中重要节点的发现
已有研究通常选取复杂网络中最为重要的节点作为其鲁棒性的测试指标,如度、介数、紧密中心性、节点效率等指标最大的节点,它们计算简单,能较为便捷地反映出各节点在网络中的重要度,但均有一定的局限性,并不能全面地反应节点在网络中的重要度[19-22]。重要度评价矩阵综合考虑了节点的局域重要性和全局重要性,能较为精准地发现网络中的重要节点[20]。因此,本文通过构建重要度评价矩阵来确定网络中的重要节点,并以其为指标测试该配送网络的鲁棒性。
定义1 节点度值指与该节点直接相连的节点数目,它是刻画和衡量节点特性的最简单但也是最重要的概念,其大小与节点的重要性正相关。
定义2 节点间最短路径长度指节点之间最短路径所包含边的数目,网络中任意两个节点间距离的最大值为网络的直径
定义3 节点效率体现了节点到其他节点的平均难易程度,定义为节点到其他节点距离的倒数之和的平均值,即:


式中,为节点总数量,为所有节点的平均度,D为节点v的度,则节点v将自身重要度的D/<k>2贡献给每个邻接节点;δ为贡献分配参数,当节点v和节点v直接相连时取1,否则取0。



利用重要度评价矩阵对该快递企业的配送网络进行评价,得到其重要度排名前10的节点信息如表1所示。
表1 配送网络节点重要度排序

Tab.1 The importance rank of nodes in distribution network
3 配送网络的鲁棒性分析
网络在遭受随机或蓄意破坏时仍能维持自身正常功能的能力称为鲁棒性,不同节点在遭受破坏时网络往往会表现出不一样的鲁棒性。为了检验配送网络在遭受破坏时的鲁棒性,本文按破坏方式将破坏分为两类:随机性破坏和蓄意性破坏。随机性破坏指在网络中随机删除10个节点;蓄意性破坏指在网络中删除10个重要度最高的节点。
复杂网络鲁棒性的评价指标主要有平均最短路径长度()、网络最大子图大小以及网络全局效率()等。为综合反映网络的局部和全局鲁棒性,本文选取平均最短路径长度和网络全局效率作为鲁棒性的评测指标。
定义5 平均最短路径长度是网络中所有节点对之间最短路径长度的平均值,即:

式中,为节点数量;c为节点到节点最短路径中包含的边的数量。
定义6是表示网络信息流通水平高低的重要指标,节点和之间的网络效率定义为这两点间最短距离d的倒数,整个网络的网络效率定义为所有节点对的网络效率的平均值,即:

式中,为节点总个数;d为节点到节点的最短路径长度。
当网络遭受某种受破坏时,若平均最短路径长度和网络全局效率变化较大,则表明网络对该类破坏表现出脆弱性;反之,则表现出鲁棒性。需要说明的是,一般情况下,删除网络的节点会减小网络的规模,从而引起网络平均最短路径长度适当的变小;但是当网络中一些作为连接桥梁的“桥点”被删除时,可能会引起网络平均最短路径长度急剧增大,甚至导致网络被分离为数个相互独立的子网络,无法计算整个网络的平均最短路径长度,此时取该网络的最大连通子图的平均最短路径长度作为替代值。
3.1 平均最短路径长度
分别对配送网络进行随机性和蓄意性破坏,其平均最短路径长度变化如图2所示。

图2 随机和蓄意性破坏下配送网络平均最短路径长度变化
由图2可知:(1)当随机删除节点时,配送网络的平均最短路径长度呈十分缓慢的变小趋势,总体上变化的数值很小,变化区间为(3.26,3.30)。其变小的原因为随着网络的节点被删除,网络规模变小,从而导致平均最短路径长度适当变小。(2)当依次删除介数最大的节点时,配送网络的平均最短路径长度呈现先逐渐增大,然后急剧变大后又适当减小的趋势,总体上变化的数值较大,变化区间为(3.30,5.80)。其逐渐增大的原因是网络中介数最大的2个节点都是网络中的“桥点”,当这2个节点被删除时会导致平均最短路径长度适当增大;其急剧变大后又适当减小的原因是当第3个节点被删除时,网络的连通性遭到破坏,网络被分为数个相互独立的子网络,取网络最大连通子图的平均最短路径长度值,从而导致平均最短路径长度值急剧变大,随着节点继续被删除,网络的规模变小,使得网络最大连通子图的平均最短路径长度值逐渐变小。
3.2 网络全局效率
分别对配送网络进行随机性和蓄意性破坏,其网络全局效率变化如图3所示。

图3 随机和蓄意性破坏下配送网络E变化
由图3可知:(1)当随机删除节点时,配送网络的网络全局效率呈几乎不变的趋势,变化区间为(0.332,0.334)。其几乎不变的原因为被删除节点的不确定性导致网络全局效率值有轻微的变化,但是整体上网络全局效率值基本维持不变。(2)当依次删除介数最大的节点时,配送网络呈现较大的变小趋势,变化区间为(0.221,0.334)。其变小的主要原因为随着网络中介数最大的节点被删除,引起网络中节点间最短路径长度增大,从而导致网络的以较大的趋势变小。
结合对平均最短路径长度和网络全局效率的分析,得到如下结论:(1)当遭受随机性破坏时,配送网络的平均最短路径长度和网络全局效率值变化很小,因此配送网络对随机性破坏表现出鲁棒性;(2)当重要度最大的节点遭受蓄意性破坏时,配送网络的平均最短路径长度和值变化很大,因此配送网络对蓄意性破坏表现出脆弱性。
4 配送网络的鲁棒性提升对策
Barabasi和Albert对大量的现实网络进行了演化机理研究,发现网络中的节点度的分布形式服从幂律分布[23],即:

由于此类网络的标度值均为,因此将此类网络称为无标度网络,谢逢洁、黄建华等将这一结论与配送网络结合,验证了快递企业配送网络的无标度特性。
Cohen等给出了无标度网络在遭受随机性和蓄意性破坏时,其鲁棒性临界值的指标[24];刘建国等在此基础上提出了在一定平均度约束下无标度网络遭受随机性破坏、蓄意性破坏以及两者同时发生时的鲁棒性优化策略[25];于国栋等在上述研究成果的基础上,构建了面向成本约束的鲁棒性最优化模型,明确了优化模型中点和边增加的策略[26]。因此,本文结合已有研究成果,构建出配送网络鲁棒性优化模型,并用Python对模型进行求解。
无标度网络在遭受随机性破坏时,其临界逾渗值为:
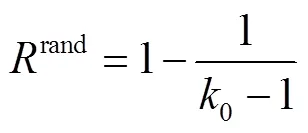
式中,0≡<02>/<0>,<0>为随机删除节点后新的度分布的平均度值,<02>为新的度分布的平方和的平均值。无标度网络的幂律分布形式也可以表示为:
值得注意的是,水利工程进度控制,是一项连续不断且循环往复的工作,工程结束前,对基本施工进度进行动态循环控制的一种控制方式。两个重要环节,一是确定进度计划,是考核项目实施状况的基础与尺子;二是进度适时调整,是控制的重要手段与核心环节,也是提高控制效率的有效方法。

式中,为常数,=,+1, ∙∙∙,,为最小度值,为最大度值。因此,0也可通过下式求得:

无标度网络在遭受蓄意性破坏时,其临界逾渗值为:


因此,配送网络的鲁棒性综合临界值total为:

式中,和分别为随机性和蓄意性破坏鲁棒性临界值权重系数,+=1。网络的鲁棒性可通过增加新的节点或者新的边来提升,但是对于快递企业而言,新增节点或者配送线路都会带来成本的增加,即节点和配送线路的增加都受制于所需投入的成本。假设新增1个节点和1条边的成本分别为v和e,新增节点和边的数量分别为v和e,企业成本限制为,则配送网络鲁棒性优化模型如下:

针对该快递企业配送网络的数据,采用度的累积分布函数P(>k)来度量综合快递网络的度分布特性,结果如图4所示。
假设随机性破坏鲁棒性临界值权重系数取0.3,蓄意性破坏鲁棒性临界值权重系数取0.7,该快递企业新增一个物流节点的成本v为10,新增一条配送路线的成本e为2,该企业的投资额度为30,则该配送网络的随机性破坏鲁棒性临界值rand= 0.9218,蓄意性破坏鲁棒性临界值delib= 0.1347,原始鲁棒性综合临界值total= 0.4495。运用python编程对上述鲁棒性优化模型求解得到v=0,e=15,增加的配送路径及其带来的鲁棒性综合临界值提升如表2所示,优化后该配送网络的rand= 0.7843,蓄意性破坏鲁棒性临界值delib= 0.3344,鲁棒性综合临界值total= 0.5144,较原始鲁棒性临界值有14.4%的提升。为进一步验证该配送网络鲁棒性的优化效果,计算优化后网络的全局效率为0.338,可见网络全局效率也得到了一定的提升。
表2 配送网络鲁棒性综合临界值变化

Tab.2 The change of comprehensive critical value of distribution network
因此,通过配送网络鲁棒性优化模型可以有效地提升网络的鲁棒性。快递企业应根据重要度评价矩阵的评价结果和鲁棒性优化模型的求解结果采取以下措施:
(1)重点注意对广州、北京、西安、成都、义乌等度和接近中心性均较大的节点的保护,通过设立相应的应急机制来提升其鲁棒性,确保在遭受破坏时各节点能正常运转、节点间的配送线路也畅通无阻。
(2)在原来配送网络的基础上,增加表2中的15条配送路线,增加节点间的相互连接关系,从而提升配送网络的鲁棒性。
5 结 论
本文以国内某快递企业的实际订单数据为基础,通过大数据处理手段得到该企业在全国范围内的配送网点和路径数据,以配送网络中物流节点所在城市为节点,城市之间的配送路径为边,绘制该配送网络的拓扑结构图;构建重要度评价矩阵,确定配送网络中的重要节点,并以其作为网络鲁棒性测试指标,以平均最短路径长度和网络全局效率作为评价指标,对该配送网络的鲁棒性进行分析,结果表明该配送网络对随机性破坏表现出鲁棒性、对蓄意性破坏表现出脆弱性;以投入成本为约束,构造鲁棒性优化模型,并运用Python对其进行求解,验证模型的可行性和有效性,并以模型求解结果为依据对该配送网络提出鲁棒性提升对策。本文既弥补了快递企业配送网络鲁棒性定量优化方法理论研究的欠缺,又为快递企业优化其配送网络的提供了理论指导,具有较大的实际意义。
[1] LIN C C, CHEN S H. The hierarchical network design problem for time-definite express common carries[J]. Transportation Reaserch Part B, 2004, 38(3): 271-283.
[2] 韦忆立, 高咏玲. 含时间约束的配送中心选址和能力规划的鲁棒优化[J]. 统计与决策, 2015(1): 49-53.
[3] 向敏, 袁嘉彬, 于洁. 电子商务环境下鲜活农产品物流配送路径优化研究[J]. 科技管理研究, 2015, 32(18): 166-183.
[4] 杨从平, 郑世珏, 党永杰. 基于配送时间及节点流量约束的快递网络优化[J]. 系统工程, 2015, 33(11): 53-59.
[5] 黄建华, 党延忠. 快递超网络模型及基于成本的优化方法[J]. 系统管理学报, 2010, 19(6): 689-695.
[6] 黄建华, 党延忠. 快递超网络模型及基于效率的优化方法[J]. 北京理工大学学报, 2010, 13(3): 68-72.
[7] 黄建华, 党延忠. 基于时间阈值的多标准快递超网络优化方法[J]. 系统工程理论与实践, 2010, 30(12): 2129-2136.
[8] 黄建华, 党延忠. 具有社区结构和子核的快递网络优化方法[J]. 系统工程理论与实践, 2014, 34(11): 2827-2836.
[9] FALOUTSOS M, FALOUTSOS P, FALOUTSOS C. On Power-Law Relationships of the Internet Topology[J]. Acm Sigcomm Computer Communication Review, 1997, 29(4): 251- 262.
[10] 孙钦东, 孙亚红. 动态短信通信复杂网络演化模型研究[J]. 西安交通大学学报, 2009, 43(6): 5-9.
[11] MOORE C, NEWMAN M. Epidemics and Perolation in Small-World Networks[J]. Working Papers, 2000, 61(5): 5678-5682.
[12] Serrano M Á, Boguñá M. Topology of the world trade web[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2003, 68(1): 98-101.
[13] XIE F, LIN J. Exploring express delivery networks in China based on complex network theory[J]. COMPLEXITY, 2014, 21(2): 166-179.
[14] 谢逢洁, 崔文田. 航空快递网络的复杂结构特性及演化机理[J]. 系统工程, 2014, 32(9): 114-119.
[15] 谢逢洁, 崔文田. 陆运快递网络的复杂结构特性及演化模型[J]. 系统管理学报, 2016(2): 364-369.
[16] 叶彭姚. 城市道路网拓扑结构的复杂网络特性研究[J]. 交通运输工程与信息学报, 2012(1): 13-19.
[17] 黄建华. 快递网络的复杂性及鲁棒性分析-以某快递企业为例[J]. 西南交通大学学报: 社会科学版, 2009, 6(10): 98-102.
[18] 党亚茹, 孟彩红. 基于复杂网络的航空货运枢纽城市研究[J]. 交通运输工程与信息学报, 2012(2): 12-18.
[19] 陆靖桥, 傅秀芬. 复杂网络的鲁棒性与中心性指标的研究[J]. 计算机应用与软件, 2016, 33(4): 302-305.
[20] 周漩, 张凤鸣. 利用重要度评价矩阵确定复杂网络关键节点[J]. 物理学报, 2011, 61(5): 50201-50207.
[21] Lewis G. Proceedings of the Proceedings of the 41st Annual Hawaii International Conference on System Sciences[J]. Hawaii International Conference on System Sciences, 2008, 6(8): 7-10.
[22] 李彦来. 物流网络结构复杂性及优化设计问题 [D]. 北京: 北京交通大学, 2011: 19-29.
[23] Barabasi A L, Albert R, Jeong H. Scale-free- characteristics of random networks: the topology of the World- WideWeb[J]. Physica A, 2000, 281(1- 4): 69-77.
[24] Cohen R, Erez K, Ben-Avraham D. Breakdown of the internet under intentional attack[J]. Physical Review Letters, 2001, 86(16): 3682-3685.
[25] 刘建国, 党延忠, 王众托. 无标度网络对随机破坏和蓄意性攻击的鲁棒性优化[J]. 现代物流学报, 2005, 19(16): 785-792.
[26] 于国栋, 杨育, 李斐, 等. 客户协同产品创新系统鲁棒性分析与优化[J]. 计算机集成制造系统, 2014, 12(20): 2926-2934.
(中文编辑:刘娉婷,英文审改:梁宏斌)
Research on Robustness and Promotion Enterprise Countermeasure of Express Network
ZHANG Jin1,2,QIN Dong1
(1. School of Transportation and Logistics, Southwest Jiaotong University, Chengdu 610031, China; 2. National United Engineering Laboratory of Integrated and Intelligent Transportation, Southwest Jiaotong University, Chengdu 610031, China)
To improve the robustness of distribution network of express enterprise with quantitative analysis, based on the order data of an express enterprise, we obtained its nationwide distribution path data and constructed the topology of its distribution network by big data processing means of web crawler, data cleaning and so on. The important nodes in the distribution network are found by important evaluation matrix, and they are used as the robustness test indicators to analyze the robustness of distribution network. The result reveals that distribution network is robust against random destruction and fragile against intentional destruction. Taking investment cost as constraint, the robustness optimization model is built, and it is solved by Python to verify it’s reliability and feasibility. Finally, some advices on how to promote the robustness of distribution network are given according to the solutions.
distribution network; complex network theory; robustness; importance evaluation matrix; robustness optimization model
1672-4747(2018)03-0007-08
N945
A
10.3969/j.issn.1672-4747.2018.03.002
2017-04-20
张锦(1963—), 男, 四川广元人, 西南交通大学教授, 博导, 主要研究方向为物流工程、物流系统规划、复杂网络。
张锦,秦东. 快递企业配送网络的鲁棒性及其提升对策研究[J]. 交通运输工程与信息学报, 2018, 16(3): 7-13, 58.

