软岩中竖井开挖的支护体系研究

孔科 易文明 汤雷 付峥

摘要：以某水电站闸门竖井为研究对象，建立了三维有限元模型。采用Mohr-Coulomb屈服准则，模拟了软岩中竖井的开挖及其支护体系，详细比较了不同支护措施下软岩的等效塑性应变与塑性区、软岩的变形及支护结构的应力等，得知在软岩中开挖竖井时宜选用衬砌混凝土作为主要的支护手段，锚杆可作临时支护。

关键词：闸门竖井；软岩；开挖支护；等效塑性应变；应力与变形；衬砌混凝土

中图分类号：TV314；TV331 文献标志码：A doi：10.3969/j.issn.1000-1379.2018.02.028

经过几十年的发展，支护体系逐步得到完善。锚杆支护是最常用的一类，主要包括锚杆（锚索）、锚喷、锚网、锚喷网、锚梁网、锚杆与支架组合支护等川，其支护形式与理论不再是消极地承受围岩压力，而是利用锚杆与围岩的共同作用，最大限度地调动和发挥围岩自身的承载能力，把围岩从施载体转化为承载体，限制围岩变形、位移和裂缝的发展，达到围护地下工程的目的[2-3]。

地下洞室的开挖使岩体中的地应力得以释放并重分布。随着开挖程度的增大，应力重分布的范围亦扩大，不能承担上部荷载的岩体产生破坏，如果不对其采取有效的支护措施，就会引发失稳[4]。随着我国西部水电开发的深入，在软岩以及覆盖层中开挖竖井的情况越来越多，开挖过程中支护体系的有效性直接决定施工、运行安全。松动圈支护理论认为，巖石破碎形成松动圈过程中产生碎胀变形的碎胀力是产生支护荷载的最主要因素，是支护的主要对象[3，5-6]；现代岩石力学中的弹塑性理论认为，围岩的弹塑性变形是支护的主要对象[7]。本文基于Mohr-Coulomb屈服准则，对某水电站闸门竖井的开挖支护过程进行了非线性有限元模拟，通过对各种支护条件下塑性应变、塑性区以及支护结构的变形与应力的比较，以支护体系的应力为安全性判定标准，研究适宜软岩中竖井开挖的支护体系。

1 计算原理

Mohr-Coulomb屈服准则反映了岩土材料在屈服时与球应力和偏应力相关的特性，在岩土工程界被广泛应用。

设σ1≥σ2≥σ3，那么Mohr-Coulomb屈服准则以主应力的形式表示为式中：c为黏聚力；φ为内摩擦角；I1为应力张量第一不变量；J2为偏应力张量第二不变量；θσ为应力Lode角；σ1、σ2、σ3分别为第一、第二、第三主应力。

2 工程算例

某水电站地处青藏高原的东南缘向川西高山峡谷地貌的过渡带，河道蜿蜒曲折，呈M形。引水隧洞所在的河谷右岸地形坡度变化较大，上部多呈陡崖，坡度为60°～70°，河谷呈不对称V形。限于河谷条件，只能在引水隧洞人口附近山体中布置闸门竖井。

2.1 计算条件及材料参数

引水隧洞闸门井开挖断面为8.5m×10.3m，垂直方向高程范围为2276.4～2394.4m，处于风化、卸荷带，岩体完整性差，结构松弛，围岩类别为V类，闸门井围岩稳定的评定和支护形式的选取是当前面临的主要难题。根据地质勘测结果，闸门井附近的岩体中无地下水，所以只需解决开挖稳定的问题。

初步研究决定，开挖过程中采用喷锚的方式加固，锁口梁采用间排距为0.4m×0.6m的6m长锚杆加固，门井的周围采用间排距为1.0m×1.0m的4.5m和6.0m长的锚杆交错布置加固，且在内表面挂网喷护20cm厚的C20混凝土。由于门井上半段地质条件较差，因此计算中单独考虑了把上半段衬砌增加至60cm厚，下段厚度保持20cm不变的工况。

计算方案如下：①无衬砌；②只有锚杆支护；③只设置20cm厚混凝土衬砌；④上段60cm结合下段20cm厚混凝土衬砌；⑤20cm厚混凝土衬砌结合锚杆支护；⑥上段60cm加下段20cm厚混凝土衬砌结合锚杆支护。根据地质研究资料，计算的材料参数见表1。根据地质勘测的结果，高程2349.23m以上的围岩结构松弛，完整性较差，计算中按V类围岩参数的下限值考虑；高程2349.23m以下的围岩按V类围岩参数的上限值考虑。

计算荷载主要为围岩与结构的自重。计算中首先对闸门井附近围岩的初始自重应力场进行了模拟，然后计算模拟了开挖与支护过程。

2.2 计算模型

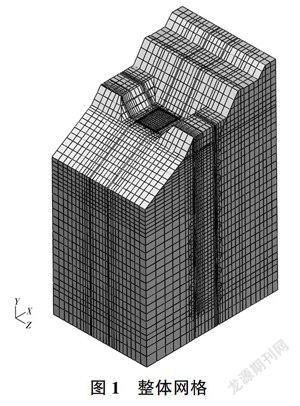
依据闸门井周围的地质条件，建立了三维有限元模型。引水隧洞顺水流水平向为X轴正向，竖直向上为Y轴正方向。模型在X方向计算范围长度为66m；Y方向范围为高程2294.4～2394.4m；Z方向计算范围长度为46.5m。有限元模型整体网格见图1。

2.3 计算结果

结构的安全控制因素比较多，根据不同的因素采取的加固措施不同。按照弹塑性力学的支护观点，锚杆必须贯穿塑性区以锚固在未产生塑性的基岩中；按照结构力学的观点，结构的变形不能超过特定的范围，且结构应力必须在可控的范围内。这里对不同支护方案下软岩的塑性区、位移及支护结构的应力进行了详细比较与分析。

2.3.1 软岩塑性区分析

在不同的支护方式下，竖井开挖结束时软岩中塑性区分布见图2～图7。在没有任何支护措施的情况下，塑性区的最大影响深度达20m，锚杆在一定程度上控制住了塑性区的深层扩展，等效塑性应变最大值减小约25%；混凝土衬砌的施加直接大幅度缩小了塑性区范围，60cm厚衬砌比20cm厚衬砌时等效塑性应变最大值减小了约34%；在增加了锚杆的情况下，塑性区的影响范围变化不明显，等效塑性应变最大值减小了约34%。因此，混凝土衬砌支护对塑性区影响特别明显，锚杆对塑性区影响较小，锚杆的支护可作为软岩开挖的前期塑性区临时控制手段，混凝土衬砌应作为安全控制的主要手段。

2.3.2 软岩位移分析

在不同的支护方式下，竖井开挖结束时闸室竖井的水平位移最大值见表2。与方案①水平位移相比，方案②使水平位移减小27.6%～29.4%，方案③使水平位移减小44.6%～51.4%，方案④使水平位移减小56.9%～66.9%，方案⑤使水平位移减小52.5%～58.2%，方案⑥使水平位移减小60.7%～67.3%。因此，闸室竖井边墙的水平位移均比较小，混凝土衬砌对洞壁变形起主要作用。

另外，由于高程2349：23m上下围岩参数不同（上低下高），因此在高程2349.23m附近围岩变形规律发生了变化。

2.3.3 结构应力分析

在不同的支護方式下，竖井开挖结束时锚杆的应力峰值见表3，衬砌混凝土应力峰值见表4。从计算结果可知，在只有锚杆支护时，锚杆应力最大，且峰值位置产生于上半段；当增加混凝土衬砌时，锚杆应力减小约36.3%；衬砌混凝土厚度从20cm增大至60cm时，锚杆的应力发生重分布，峰值产生位置从上下两个峰值区域转变为只有下段一个峰值区域（下段衬砌厚度20cm不变）。因此，增加衬砌对软岩应力的分布影响较明显。

衬砌上的拉应力主要产生于衬砌拐角外侧，在上半段基岩较差段应力较大；增加衬砌的厚度对衬砌的应力峰值影响明显，增加衬砌厚度使拉应力峰值最大减小约63%；增加锚杆使衬砌混凝土的拉应力减小约10%。

3 结论

通过对软岩中竖井开挖各种支护方式的比较，可得出以下结论：

（1）锚杆的作用对软岩中塑性区的发展影响有限；混凝土衬砌对塑性区影响较大，在软岩塑性稳定方面应以混凝土衬砌为主。

（2）门井结构三维效应明显，塑性应变较小，虽然塑性区范围较大，但软岩变形较小；锚杆对软岩的变形影响相对较小，混凝土衬砌影响更明显。

（3）混凝土衬砌可直接影响软岩的应力分布，从而进一步影响锚杆的应力，当衬砌达到一定厚度时锚杆中的应力趋于不变；随着衬砌厚度的增加，衬砌上的应力有较大程度的减小，锚杆对衬砌的应力影响较小。

（4）混凝土衬砌对软岩塑性区、软岩变形及软岩的应力影响非常明显，而锚杆的支护效果有限，在软岩竖井开挖中宜选用混凝土衬砌作为主要支护措施，锚杆可作为临时开挖稳定支护措施。

参考文献：

[1]陆士良，汤雷，杨新安.锚杆锚固力与锚固技术[M].北京：煤炭工业出版社，1998：1-17.

[2]张社荣，顾言，张宗亮.超大型地下洞室围岩锚杆支护方式的优化设计[J].水力发电学报，2007，26（5）47-52.

[3]毕远志，朱赞成.利用松动圈原理确定锚杆支护参数的方法[J].江南大学学报（自然科学版），2006，5（2）：241-245.

[4]于学馥，郑颖人，刘怀恒，等.地下工程围岩稳定分析[M].北京：煤炭工业出版社，1983：2-28.

[5]董方庭.巷道围岩松动圈支护理论及应用技术[M].北京：煤炭工业出版社，2001：35-40.

[6]杨林德.岩土工程问题的反演理论与工程实践[M].北京：科学出版社，1999：101-104.

[7]张金耀，岐红升，王玉海.松动圈测试在巷道支护设计中的应用[J].山西煤炭，2003，23（2）：37-38.