凌汛期地面温度精细化预报方法研究
徐幼平 杜海龙 胡邦辉 原韦华 张季平

摘要:气温的精细化预报对防凌减灾具有重要意义。基于AREM数值模式预报产品,利用2006-2010年黄河凌汛期(11月至翌年3月)实测温度进行建模,对2009-2010年度凌汛期黄河内蒙古河段周边4个站点的每3h地面温度进行精细化预报研究。6个精细化预报方案效果比较表明:各预报方案都能改进模式预报效果,效果最好的是逐步回归方法。逐步回归方法对各站3~72h平均预报的平均绝对误差降低1.47℃,1℃准确率提高 14.6%,2℃准确率提高26.1%;改进效果最明显的站点是准格尔站,改进后的72h预报的平均绝对误差为1.25℃,1℃准确率为46.5%,2℃准确率为80.2%。
关键词:凌汛期;AREM模式;气温;精细化预报;黄河内蒙古河段
中图分类号:P457;TV882.1 文献标志码:A doi:10.3969/i.issn.1000-1379.2018.02.007
黄河内蒙古重点防凌河段(三湖河口至头道拐)在特殊的地理位置和气象水文条件的共同影响下,每年冬季都发生凌汛灾害。凌汛发生主要受热力因素、动力因素、河势因素和人类活动影响,其中热力因素是黄河凌汛发生发展的主要影响[1-2]。气温是热力因素的综合表征,关于温度变化[3-5]和寒潮[6]对凌汛影响的研究表明,气温的剧烈变化对河段封、开河的速度和次数有重要影响。
气温的精细化预报可以很好地反映气温的变化趋势,进而反映凌汛发展的趋势。凌汛期气温预报对黄河防凌减灾工作具有重要意义,但是现阶段关于凌汛期气温精细化预报的研究较少,无法满足防凌工作所需的气象要素保障。笔者基于AREM(Advanced Re-gional Eta-coordinate Model)数值预报模式,利用2006-2010年凌汛期(11月至翌年3月)资料,对黄河内蒙古重点防凌河段周边的4个站点进行气温的精细化预报研究,以提高凌汛期气温预报水平。
1 模式简介
温度精细化预报模式为AREM模式,该模式以有限区域η坐标数值模式(REM)为基础,充分考虑我国复杂地形,采用先进的计算方法和处理技巧,有效地解决了复杂地形带来的计算问题[7]。黄河内蒙古河段周边地形复杂,利用AREM模式进行数值预报具有一定的优势。本研究使用AREM2.5.0版本进行模拟,水平分辨率为37km,垂直分层不等距分为42层,初始模拟范围为中国范围(北纬14°-51°、东经74°-136°)。起始预报时间为00时(UTC),预报时效为72h,时间分辨率为3h。模式所用物理过程为BIAM显示冷云预报方案,行星边界层参数化方案为非局地边界层方案,地表通量参数化方案为多层结通量一廓线方案,地表辐射参数化过程为Benjamin参数化过程。将地面常规资料、探空资料与预报时次相对应的NCEP再分析资料进行融合,作为模式模拟的初始场。时变侧边界条件由NCEP再分析资料提供,每6h更新一次。
2 资料和方法
2.1 资料介绍
选取黄河内蒙古河段周边4个站点(见图1)进行气温精细化预报,预报时效为3~72h,时间分辨率为3h。模式模拟的资料长度为2006-2010年凌汛期(11月至翌年3月),其中:2006-2007年度、2007-2008年度、2008-2009年度为建模或训练样本(454个),2009-2010年度为检验样本(151个)。预报所需的资料是从原始模拟范围内提取的内蒙古防凌河段(北纬38.5°-41.5°,东经108.5°-112.5°)的数据。气温预报所需的初始预报因子来自AREM模式预报的23个基本要素场(温度、降水量、比湿、位势高度、U分量、V分量、涡度、散度、垂直速度等)和由这些基本要素计算得到的58个诊断量(24h变温、变高、虚温、温度平流等)共81个预报因子,选取距站点最近的格点值作为站点预报值。所用的实测资料为包头、托克托、准格尔、清水河四站气温资料,时间长度和时间分辨率与模式资料一致。
2.2 预报方法
本研究温度精细化预报所用的方法包括滑动偏差订正方法、逐步回归法和BP神经网络方法。其中:滑动偏差订正法属于模式输出预报方法(DMO法),逐步回归法属于统计预报方法(MOS法),而BP神经网络属于人工智能方法。
2.2.1 滑动偏差订正方法
滑动偏差订正法就是利用近期的观测资料计算近期的预报误差,并近似作为预报的系统误差,在后面的预报中进行扣除,以提高预报准确率[8]。本研究利用“最易系统估计值”(Best Easy System estimator,BES)[9]计算近期的预报误差,BES不受极端值影响,能很好地反映模式预报的系统误差,其计算式为
BES=(Q1+2Q2+Q3)/4(1)式中:Q1、Q2、Q3分别为距离预报时间最近n天预报偏差的第一、第二、第三四分位数。四分位数就是把所有数值由小到大排列并分成四等份,处于3个分割点位置的数即四分位数。第一、二、三四分位数分别是将样本中所有数值由小到大排列后第25%、50%和75%的位置所对应的数值。
温度预报公式为
F=Fm-BES(2)式中:F为利用滑动偏差订正方法得到预报值;Fm为模式预报值。
3~30d历史样本试验结果表明,当历史样本为25~30d时,72h预报值的平均绝对误差趋于常数,系統误差值达到稳定。本研究选取预报时间对应的前30d的预报偏差近似为模式系统误差,并在预报中减去该误差,得到相应的预报值。
2.2.2 逐步回归预报方法[10]
利用MOS统计方法,建立温度的统计预报方程,方程形式为
y=b0+b1x1+b2x2+…+bnxn(3)式中:y为由各个预报因子x1,x2,…,xn线性组合得到的预报值;b1,b2,…,bn为回归系数;b0为回归常数。
为了保证各因子之间相互独立,采用双重检验逐步回归方案,计算因子方差贡献和求解回归系数同时进行,以保证所得方程中的所有因子都是显著的。根据本研究要求,逐步回归方法进行预报因子引入和剔除的临界F检验值取2.64。
2.2.3 BP神经网络方法[11]
BP神经网络是目前研究最成熟、应用最广泛的人工神经网络模型之一。BP神经网络具有自学习、自组织、自适应和很强的非线性映射能力,可以以任意精度逼近任意连续函数。BP神经网络由输入层、隐层和输出层组成,隐层可以为单层或多层。BP神经网络的学习过程由前向计算过程和误差反向传播过程组成。在前向计算过程中,输入量从输入层经隐层逐层计算,并传向输出层,每层神经元的状态只影响下一层神经元的状态。如输出层不能得到期望的输出,则转人误差反向传播过程,误差信号沿原来的链接通路返回,逐次调整网络各层的权值和阈值,到达输入层,再重复前向计算。这两个过程反复进行,不断调整各层的权值和阈值,使得误差最小或达到人们所期望的要求时,学习过程结束。
本研究使用3层BP神经网络,隐层只有一层。热流量方程选取因子方法和相关系数选取因子方法的输入层、隐层、输出层的节点数分别为7个、3个、1个。主分量分析筛选因子的BP神经网络预报方案(方案五)的隐层节点数是输入层节点数(主分量个数)的1/2取整后的结果,输出层节点数为1个。BP神经网络的动量因子取0.05,学习率为0.8,训练次数为20000次,期望误差临界值为2.5×10-3。
2.3 检验方法
温度是连续型变量,检验方法为平均绝对误差和预报准确率[12]。
平均绝对误差(Mean Absolute Error,MAE):為5个方面:局地温度(2m高处温度、地面温度)、温度平流(温度平流、南北风)、垂直运动(垂直速度)、非绝热因子(降水量、24h变温)、与气温日变化有关的因子(地面气压、相对湿度、地面风速、温度露点差、稳定度指数)。从上面与气温日变化有关的因子中选取3个预报因子,而在其余4个方面各选取1个预报因子,最终选取7个因子作为逐步回归和BP神经网络建模训练的预报因子。
2.4.2 主分量因子筛选法
主分量分析即经验正交分解(EOF分解),是一种有效的多变量分析方法。采用主分量分析方法对数据场进行降维处理,可以用少量的主分量来最大限度地反映预报因子的信息[11]。首先选出相关系数大于0.2的预报因子作为主分量分析的初选因子,再对初选因子进行主分量分析,并以累计解释方差百分率达到85%时的主分量作为预报因子,进行建模预报。
2.4.3 相关系数筛选法
首先选取相关系数较大的25个预报因子,并将相关系数最大的作为第一预报因子;计算其余预报因子与第一预报因子的相关系数,选取相关系数最小的作为第二预报因子;第三预报因子为与第一和第二预报因子相关系数之和最小的因子;依此类推,直到选出7个预报因子为止。由于选取的25个预报因子之间的相关系数较大,不利于逐步回归方法建模,故相关系数筛选法只用于BP神经网络方法。
2.5 预报方案设计
根据前面对预报方法和因子筛选方法的分析,本研究设计6个预报方案进行凌汛期地面温度精细化预报研究(见表1)。方案一为滑动偏差订正方法,方案二、三为不同预报因子选取方案的逐步回归方法,方案四、五、六为不同预报因子选取方案的BP神经网络方法。
3 结果分析
首先分别比较并选出逐步回归和BP神经网络在不同预报因子选取方案下预报效果最好的方案,然后利用最优的逐步回归和BP神经网络方案与滑动偏差订正方法比较,最终选出适合于黄河四站的温度预报方案。由于四站研究结果类似,因此本研究在逐步回归、BP神经网络预报效果比较和最优预报方案选取中,只给出包头站的选取结果。而对于各方案在3-72h的平均预报效果选取中,则给出了所有站点的选取结果。
3.1 逐步回归方法预报效果比较
图2给出了逐步回归方法(方案二、方案三)对包头站的预报效果比较,TEM表示根据热流量方程筛选预报因子的方案,EOF表示主分量因子选筛选报因子方案。从图2可以看出逐步回归方法预报的温度误差具有24h的周期性,预报误差在3~15、27~39、51~63h时快速增长,而在15~24、39~48、63~72h时达到最大并趋于平缓;相应的预报准确率呈减小趋势,1℃准确率在30%~50%之间,2℃准确率在50%~80%之间。比较逐步回归方法的两种方案可知,两种方法预报的平均绝对误差接近,而从1℃和2℃准确率比较可知,除个别时次,主分量因子选取方案(方案三)优于热流量方程选取因子方案(方案二)。
3.2 BP神经网络方法预报效果比较
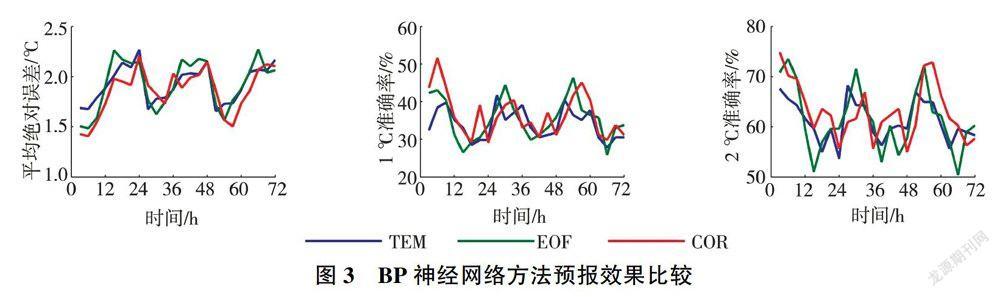
图3给出了BP神经网络方法(方案四、五、六)在不同因子选取方案下的预报效果比较。TEM表示根据热流量方程筛选预报因子,EOF表示主分量分析筛选预报因子,COR为相关系数法筛选预报因子。从图3可以看出,BP神经网络预报的误差和准确率也具有24h周期性的特点,1℃准确率在30%~40%之间,2℃准确率在50%~75%之间。除27、30、33、51、69、72h外,方案六的平均绝对误差较其他两种方案低。3种预报因子选取方案的1℃准确率和2℃准确率交叉分布,不同时次的准确率不一样,方案四的准确率在27、36h时较高,方案五的准确率在33、54h时较高,方案六准确率在6、21、45、57h时较高。整体而言,相关系数法筛选因子建立的BP神经网络模型(方案六)预报效果最好。
3.3 最优预报方案的选取
上文分析可知,方案三和方案六分别是逐步回归和BP神经网络的最优预报方案,适合于包头站最优温度预报方案则通过方案三、方案六和滑动偏差订正法(方案一)的比较得出。图4给出了滑动偏差订正法和前两种最优预报方案的比较。图4中BES表示滑动偏差订正法,SWR表示逐步回归方法,BP表示BP神经网络方法。由于本研究只预报2009-2010年度凌汛期(11月至翌年3月)地面温度,而滑动偏差订正法需要过去30d的温度预报值进行系统误差的计算,即2009年11月的温度订正需要2009年10月温度预报值,因此用2008年11月的温度预报值代替2009年10月的温度预报值进行模式系统误差的计算。
从图4可以看出,滑动偏差订正法较逐步回归和BP神经网络的预报效果差,平均绝对误差最大接近2.5℃,1℃准确率和2℃准确率在3种方法中较低。逐步回归方法的平均绝对误差和准确率与BP神经网络的大部分接近,但是在27、30、51、54h时,逐步回归方法的平均绝对误差、1℃准确率和2℃准确率明显优于BP神经网络的。总体来看,预报效果最好的是主分量分析筛选预报因子的逐步回归方法(方案三)。
3.4 72h的平均预报效果比较
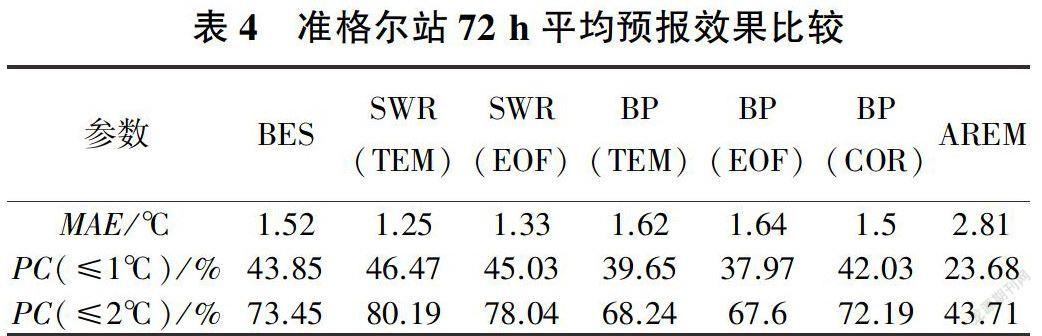
表2~表5分别为包头、托克托、准格尔、清水河四站72h的平均预报效果比较,表中的方案同表1的方案一致,AREM表示原始模式预报结果。从表2可以看出:方案三的平均绝对误差为1.81℃,略高于方案二的1.78℃,而方案三的1℃准确率为36.95%,2℃准确率为65.95%,为各方案中最高的,故包头站预报效果最好的是方案三。其他三站的比较结果较为明显,托克托站(见表3)预报效果最好的是方案二,平均绝对误差为1.59℃,1℃准确率为38.47%,2℃准确率为68.74%;准格尔站(见表4)预报效果最好的是方案二,平均绝对误差为1.25℃,1℃准确率为46.47%,2℃准确率为80.19%;清水河站(见表5)预报效果最好的是方案二,平均绝对误差为1.61℃,1℃准确率为38.85%,2℃准确率为70.62%。从AREM模式預报结果可以看出,AREM模式对四站预报的温度平均绝对误差较大,预报准确率较低,误差系统性较为明显。本研究所用6个方案的改进效果均为正,均不同程度地提高了温度预报水平。
表6给出了各站最优预报方案相对原始模式预报的改进效果。从表6可以看出,各站平均绝对误差降低1.3℃以上,1℃准确率提高10%以上,2℃准确率提高20%以上。改进效果最明显的是准格尔站,平均绝对误差降低了1.56℃,1℃和2℃准确率分别提高了22.79%和37.48%,而改进后3项参数依次为1.25℃、46.47%和80.19%。
4 结论
为了提高黄河凌汛期气温精细化预报水平,本研究基于AREM模式,利用2006-2010年凌汛期模式产品,对黄河内蒙古重点防凌河段周边4个站点的地面温度进行精细化预报研究,通过6个方案的预报结果比较,得到以下结论。
(1)使用的6个预报方案对原始模式预报均有不同程度的改进,改进效果都为正。从四站预报的结果比较可知,逐步回归方法优于滑动偏差订正方法和BP神经网络方法。包头站在主分量分析方法选取预报因子时的预报效果最好,其余三站则在热流量方程选取因子方法时的预报效果最好。
(2)各站最优方案相对原始模式预报效果提高明显,72h预报的平均绝对误差减小了1.47℃,1℃准确率平均提高了14.60%,2℃准确率平均提高了26.13%;
(3)四站预报改进最明显的是准格尔站,72h预报的平均绝对误差、1℃准确率、2℃准确率分别为1.25℃、46.47%、80.19%。
参考文献:
[1]陈守煌,冀洪兰.冰凌预报模糊优选神经网络BP方法[J].水利学报,2004,35(6):114-118.
[2]可素娟,钱云平,郝守英,等.万家寨水库凌情特点及初始封河期调度方案研究[J].冰川冻土,2005,24(2):209-213.
[3]方立,冯相明.凌期气温变化对河段封开河的影响分析[J].水电能源科学,2007,26(6);4-6.
[4]姚惠明,秦福兴,沈国昌,等.黄河宁蒙河段凌情特性研究[J].水科学进展,2007,18(6):893-899.
[5]孟闻远,郭颖奎,王璐.黄河冰凌特点及防治措施[J].华北水利水电学院学报,2010,31(6):27-30.
[6]王春青,ARTHUR E Mynett,张勇,等.黄河流域寒潮天气与凌情关系分析[J].水文,2012,32(5):48-52.
[7]宇如聪,徐幼平.AREM暴雨数值预报模式[R].北京:中科院大气物理研究所,2004:6-7.
[8]赵声蓉,赵翠光,赵瑞霞,等.我国精细化客观气象要素预报进展[J].气象科技进展,2012,2(5):12-21.
[9]WOODCOCK F,ENGEL C.Operational Consensus Forecast[J].Weather and Forecasting,2005,20(1):101-111.
[10]黄嘉佑.气象统计分析与预报方法[M].北京:气象出版社,2004:58-70.
[11]张青贵.人工神经网络导论[M].北京:中国水利水电出版社,2004:67-91.
[12]孔玉寿,钱建明,臧增亮.统计天气预报原理与方法[M].北京:气象出版社,2010:495.
[13]朱乾根,林锦瑞,寿绍文,等.天气学原理和方法[M].北京:气象出版社,2000;29.

