横向磁场下环形液池热毛细—浮力对流

吕海慧 王霞 阳宏 闵中强

摘 要：为了解横向磁场作用下环形液池内热毛细-浮力对流的基本特性，利用有限体积法对磁场强度分别为0、0.3T和0.5T进行了三维数值模拟。结果表明：当温差分别为5K、10K时，无磁场条件下，对流为稳态流动，在外加磁场的条件下，随着磁场的增加，对流失去稳定性，变为规则的振荡对流；进一步增大磁场，对流转变为无规则振荡对流。

关键词：环形液池；横向磁场；热毛细-浮力对流；数值模拟

中图分类号：TK124 文献标识码：A 文章编号：1003-5168（2018）23-0135-06

Thermocapillary-buoyancy Convection in Annular Fluid

Pool under Transverse Magnetic Field

LYU Haihui WANG Xia YANG Hong MIN Zhongqiang

（College of Mathematical Sciences and Engineering， Anhui University of Technology，Maanshan Anhui 243032）

Abstract： In order to understand the basic characteristics of thermocapillary-buoyancy convection in the annular fluid pool under the effect of transverse magnetic field， the finite volume method was used to simulate the magnetic field strength of 0， 0.3T and 0.5T， respectively. The results showed that when the temperature difference was 5K and 10K respectively， the convection was steady flow under the condition of no magnetic field. With the addition of magnetic field， the convection lost its stability and becomes regular oscillating convection. With increasing magnetic field， convection became irregular oscillatory convection.

Keywords： annular fluid pool；transverse magnetic field；thermocapillary-buoyancy convection；numerical simulation

1 研究背景

在晶体生长过程中，熔体对流对晶体质量有着至关重要的影响。一般来说，希望得到性能均匀的晶体材料，但是，如果熔体的运动是非稳定的，则晶体的均匀性就会受到破坏。熔体流动的扰动产生湍流会造成熔体剧烈的温度波动，晶体生长速度也将会随温度的变化产生波动，导致晶体中产生生长条纹。外加横向磁场，对流会做切割磁感线运动，产生安培力，削弱流体运动，减小熔体的温度波动，从而减少晶体中的生长条纹，这使晶体的结构更加完整，晶体的质量也得到改善。

李友荣等[1]在环形浅液池内采用渐近线方法获得浮力-热毛细对流的近似解析解，得到了主流区速度场和温度场的表达式。石万元等[2]进行非稳态三维数值模拟浮力对水平温度梯度作用下环形液池内的热毛细对流，发现在深液池内，当温差超过临界值时，在常重力条件下，轴对称稳态流动将转化为三维稳定流动。周小明等[3]研究了大尺度环形液池中双层流体系统在内外壁面温差加熱下的热毛细对流不稳定性，对大小热毛细对流的振荡产生于内壁面附近，并沿着温度梯度相反的方向传播。Chen等[4]利用三维直接数值模拟环形池中毛细管比对热溶质毛细管-浮力对流。Kimura[5]等研究了横向磁场对直径为20mm的掺杂硅单晶浮区法生长过程的影响。宇慧平等[6，7]利用两维数值模拟了垂直磁场和勾形磁场作用下大直径晶体的生长情况，结果表明，垂直磁场能抑制熔体中的径向对流，当磁场强度过高时，湍流程度也增加；随着勾形磁场强度增加，熔体内的紊流得到了有效抑制。Kalae[8]利用三维数值研究了直径为400mm的单晶硅生长过程中施加水平磁场和勾形磁场的抑制效果，外加磁场可以有效地控制熔体湍流，减小熔体的热量波动。年夫雪等[9]利用三维数值模拟了水平磁场下45.72cm（18in）直拉硅单晶生长工艺，分析了不同强度水平磁场作用下熔体和晶体中的温度场分布、熔体中流场的变化及其对晶体生长固液界面形状的影响及其变化规律。Huang[10]等研究了横向磁场和勾形磁场对热毛细对流及自由液面变形的影响。上述研究表明，在晶体生长过程中，外加磁场可以有效控制熔体对流。本文利用三维数值模拟了横向磁场作用下环形液池热毛细-浮力对流。

2 物理数学模型

重力环境下g=9.8m/s2，本文所采用的直拉单晶生长模型如图1所示。液池外壁半径为rc=0.04m，内壁半径为ri=0.02m，高h=0.02m。上下表面为绝热状态。

[Z][ri][rc][h]

图1 物理模型

物理模型的简化如下：①流体为不可压缩的牛顿型粘性流体；②流体密度变化满足Boussinesq近似，流体表面张力是温度的线性函数，其他物性保持不变；③自由表面为平面且不发生变形；④上表面和底面绝热且所有壁面都为电绝缘壁面。

基于上述假设，环形液池内硅熔体的流动控制方程可表示为：

[1r×?ru?r+?v?z+1r×?w?θ=0] （1）

[?u?x+u?u?r+v?ur?θ+v?ur?z-w2r=-1ρ×?p?r+v1r×??rr?u?r+1r2×?2u?θ-2r2×?w?θ-ur2+1ρJθBz-JzBθ]（2）

[?v?t+u?v?r+w?v?r?θ+v?ur?z=-1ρ×?p?z+v1r×??rr?u?r+1r2×?2u?θ2+?2v?z2+gβT-Tref+1ρJrBθ-JθBr] （3）

[?w?t+u?w?r+v?wr?θ+v?w?z-uvr=-1ρ×?pr?θ+v1r×??rr?u?r+1r2×?2w?θ2+?2w?z2+2r2×?w?θ-wr2+1ρJzBr-JrBz] （4）

[?T?T+u?T?r+wr×?T?θ+v?T?z=-kρCp1r×??rr?T?r+1r2×?2T?θ+?2T?z2] （5）

其中，u、v、w分别表示r、z和[θ]方向的速度，[ρ]为密度，p为压力，T为温度，Tref为Boussinesq假设中的参考温度，Cp为比热容，[μ]为流体动力黏度，v为运动黏度系数，k为流体的导热系数，J为诱导电流，B为磁场强度。

电磁感应方程可以通过Maxwell方程和Ohm定律推导出来：

[?b?t+V×?b=1μmσm?2b+B0+b×?V] （6）

其中，V表示速度矢量，B为磁场强度，等于外加磁场[B0]和诱导磁场b之和，[σm]为电导率，[μm]为磁导率。诱导电流通过式（7）获得：

[J=1μm?×b] （7）

洛伦兹力表示为：[F=J×B]。

硅熔体物性参数见表1。

表1 硅熔体物性参数

[参数 符号 数值 密度（kg·m-3） [ρ] 2.53×103 动力黏度（kg·m-1·s-1） [μ] 7×10-4 导热系数（W·m-1·K-1） k 64 热容量（J·kg-1·K-1） CP 1×103 电导率（Ω-1·m-1） [σm] 1×106 磁场强度/T B0 0，0.3，0.5 磁导率 [μm] 1.257×10-6 ]

3 计算方法

采用非均匀结构化交错网格的有限体积法对控制方程进行离散，对动量方程、能量方程中的对流项采用二阶迎风格格式离散，对流项采用二阶迎风格离散，扩散项都采用二阶中心差分离散，时间项采用二阶隐式推进法，压力速度耦合采用SIMPLE算法。本文计算区域划分为25.6万个网格，计算中采用时间步长为5×10-3s。迭代求解过程中，当速度、温度、压力等变量相对变化率小于10-5时认为计算已收敛。

4 结果与分析

4.1 温度分布

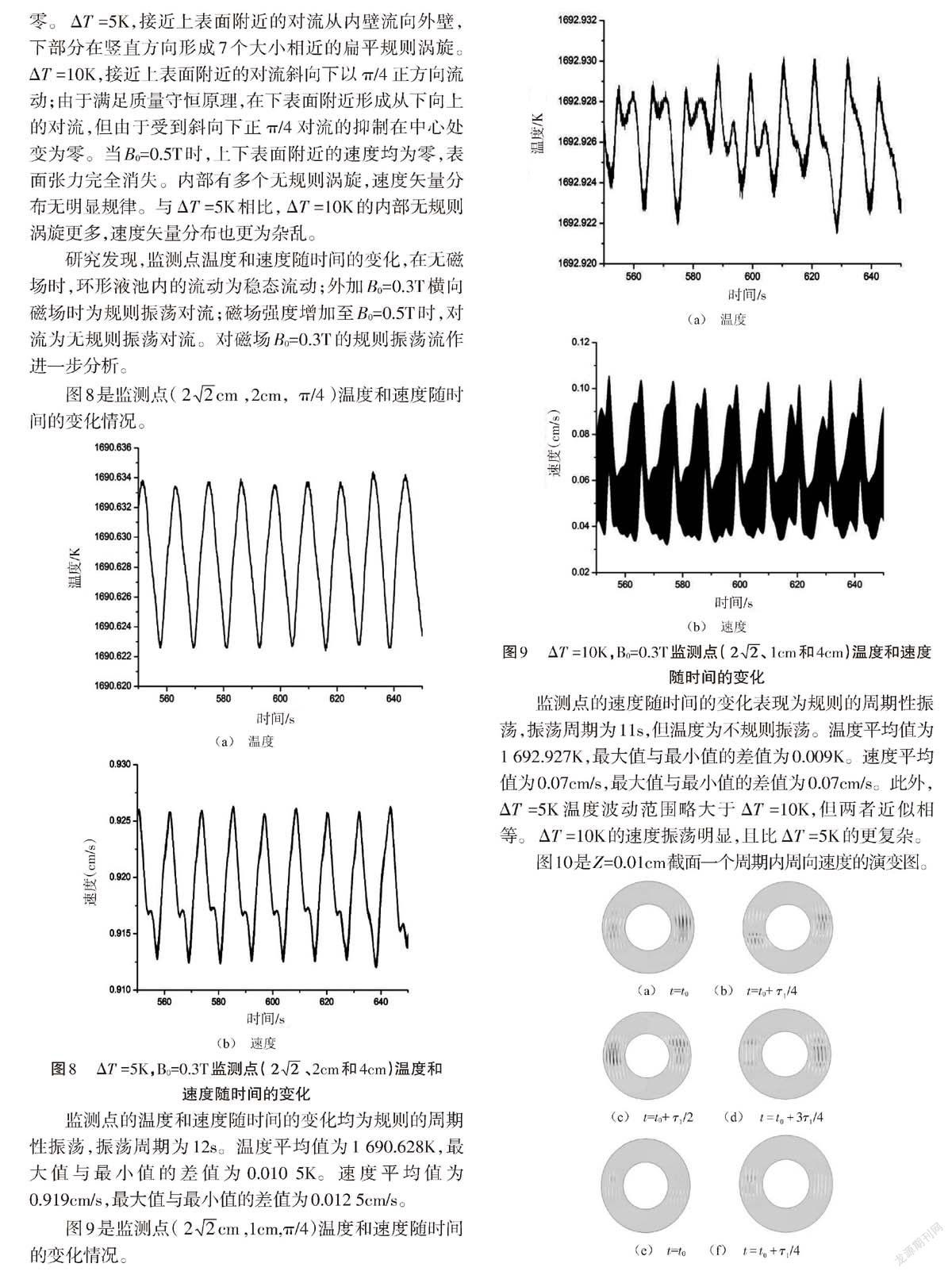
图2是上表面温度等值线分布。

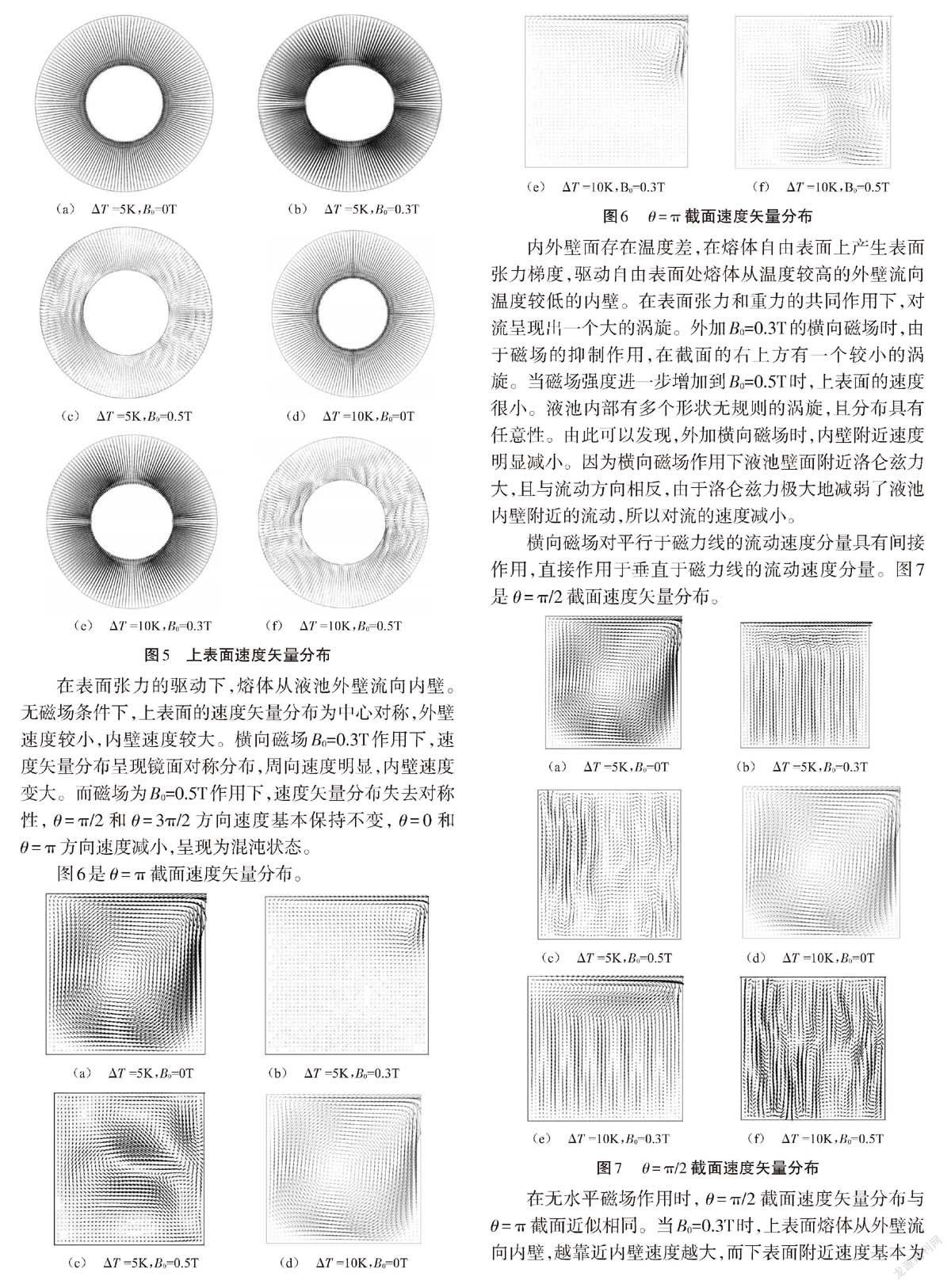
（c） [ΔT]=5K，B0=0.5T （d） [ΔT]=10K，B0=0T

（e） [ΔT]=10K，B0=0.3T （f） [ΔT]=10K，B0=0.5T

图6 [θ=π]截面速度矢量分布

内外壁面存在温度差，在熔体自由表面上产生表面张力梯度，驱动自由表面处熔体从温度较高的外壁流向温度较低的内壁。在表面张力和重力的共同作用下，对流呈现出一个大的涡旋。外加B0=0.3T的横向磁场时，由于磁场的抑制作用，在截面的右上方有一个较小的涡旋。当磁场强度进一步增加到B0=0.5T时，上表面的速度很小。液池内部有多个形状无规则的涡旋，且分布具有任意性。由此可以发现，外加横向磁场时，内壁附近速度明显减小。因为横向磁场作用下液池壁面附近洛仑兹力大，且与流动方向相反，由于洛仑兹力极大地减弱了液池内壁附近的流动，所以对流的速度减小。

横向磁场对平行于磁力线的流动速度分量具有间接作用，直接作用于垂直于磁力线的流动速度分量。图7是[θ=π/2]截面速度矢量分布。

（a） t=t0 （b） t=t0+[τ1/4]