基于遗传算法的宽带匹配电路优化设计

王鹏

摘 要：在不同特性阻抗传輸线连接，或微波传输线的负载不匹配时，连接处会产生反射，为了消除反射，使阻抗匹配，可以加入阻抗变换器。单节阻抗匹配器结构简单，但工作带宽窄；多节变换器可以拓宽工作带宽。一般来说，节数越多，带宽越宽，随之而来的就是变换器越长。本文提出了一种基于遗传算法的优化设计方法，并与二项式响应设计仿真对比，在多节数、大宽带、大失配负载下反射系数有更好的表现。

关键词：遗传算法；宽带；阻抗匹配；多节；阻抗变换器

中图分类号：TP183 文献标识码：A 文章编号：1003-5168（2018）07-0143-03

Optimized Design of Broadband Matching Circuit

based on Genetic Algorithm

WANG Peng

（China Airborne Missile Academy，Luoyang Henan 471000）

Abstract： Reflection appears when transmission lines connect with different character impedance or load mismatch happens. Impedance transformer can be used for eliminating reflection. The structure of single section impedance matching circuit is simple， but result in narrow band behavior. Multi-section transformer can improve the bandwidth. In general， wider bandwidth increases with the number of sections， hence the length of transformer would be longer. This paper described an optimized design based on genetic algorithm. Comparing with binominal transformer， the reflection of the circuit designed by GA has a better performance on cascaded multi-section， wider bandwidth and higher rate of load mismatch.

Keywords： GA；genetic algorithm；broadband；impedance matching

1 研究背景

在设计微波元器件时，经常会面临当两段微波传输线尺寸不同时，或者介质不同时，其特性阻抗也就不同，或者传输线和负载不匹配，当相互连接时，由于阻抗不匹配就会在连接处产生反射。这时会使得在传输线中产生的损耗增加，降低传输效率；降低负载从微波源获得的最大功率；会在传输线中产生驻波，从而限制传输效率，降低功率容量；也会影响微波测量时测量数据的准确性和可靠性等。因此，消除反射对微波传输系统是一个重要的要求。为了消除不良反射现象，可在其间接入一阻抗变换器，以获得良好的匹配。

四分之一波长变换器对于匹配实数负载阻抗到传输线，是简单而有用的电路，其主要特点是能以有规律的方式应用于较宽带宽的多节变换器的设计。随着微波技术的发展，更大的带宽、更低的反射系数和更小的电路尺寸成为设计中的重点。本文提出了一种基于遗传算法的优化设计方法，在大宽带、大失配条件下反射系数拥有更好的性能表现。

2 宽带匹配电路设计

2.1 多节阻抗变换器

四分之一波长的阻抗变换器结构简单，由于受可接受的最大反射系数限制，工作带宽较窄。为拓宽工作带宽，可以采用多节四分之一波长变换器相接[1]。

图1为N节四分之一波长阻抗变换器，每节电长度均为[θ]，其特性阻抗分别为[Z1]，[Z2]，[Z3]，…，[Zn]，…，[ZN]，分别接在特性阻抗为[Z0]和[ZL]的两段之间达到宽带匹配。其总反射系数可近似为（忽略多重反射）：

[Гin=n=0NГne-2njθ] （1）

其中

[Г0=Z1-Z0Z1+Z0，Гn=Zn+1-ZnZn+1+Zn，ГN=ZL-ZNZL+ZN] （2）

进一步假定该变换器是对称的，即[Г0=ГN，Г1=ГN-1，Гn=ГN-n，]…，则式（1）可写为：

[Гin=2e-2NjθГ0cosNθ+Г1cosN-2θ+…+ГN-12cosθ] （3）

[Гin=2e-2NjθГ0cosNθ+Г1cosN-2θ+…+ГN2] （4）

其中，式（3）中的N为奇数，式（4）中的N为偶数。

2.2 二项式多节匹配变换器

二项式（最平坦）响应是带通响应多节变换器常用设计之一[3]。通过设置在中心频率f0处[Гin]的前N-1阶导数为0，能得到：

[Гin=A（1+e-2jθ）N] （5）

[Гin=2NAcosθN] （6）

式中，A为常数。当f=0时，所有节的电长度均为0，即有：

[Гin（0）=2NA=ZL-Z0ZL+Z0] （7）

[A=2-NZL-Z0ZL+Z0] （8）

按照二项式将式（7）和式（8）展开为：

[Гin=An=0NCNne-2njθ] （9）

[CNn=N！（N-n）！n！]是二项式系数。因[CNn=CNN-n]，由式（1）和式（8）可得：

[Гn=ACNn] （10）

假定[Гn]较小，可以用近似法将式（2）写成：

[Гn=Zn+1-ZnZn+1+Zn≈12lnZn+1Zn] （11）

于是结合式（2）和式（11）可给出：

[lnZn+1Zn≈2ACNn=21-NZL-Z0ZL+Z0≈2-NCNnlnZLZ0] （12）

此时，各节的特征阻抗[Zn]便可求得。这种方法确保有自身一致性的优点，而且在给定节数情况下，二项式匹配变换器的通带响应是最佳的，在接近设计频率处，响应会尽可能地平坦。

3 遗传算法

遗传算法（Genetic Algorithm，GA）是在模拟达尔文的自然选择和遗传变异的生物进化论的基础上迭代自适应概率搜索算法。在遗传算法中，一组字符串（称为染色体或基因）用一种编码表示（二进制或其他方法），即一群候选解（称为个体），染色体是主要的进化对象，像生物进化一样有继承（inheritance）、变异（mutation）、选择（selection）和交叉（crossover）[3]。

在遗传算法中，候选解进化通常从随机种群产生的个体（初始解）开始，并发生在之后的每一代中。在每一代中，评估每个种群的个体适应性，要从当前种群中随机选择多个个体（根据其适用度选择最优值），修改（交叉并可能随机突变）并形成新的种群。新的种群则用于下一个迭代的算法。通常，当达到最大迭代代数时或者达到满意的适应度时，该算法就结束了[4]。

3.1 基于遗传算法的设计

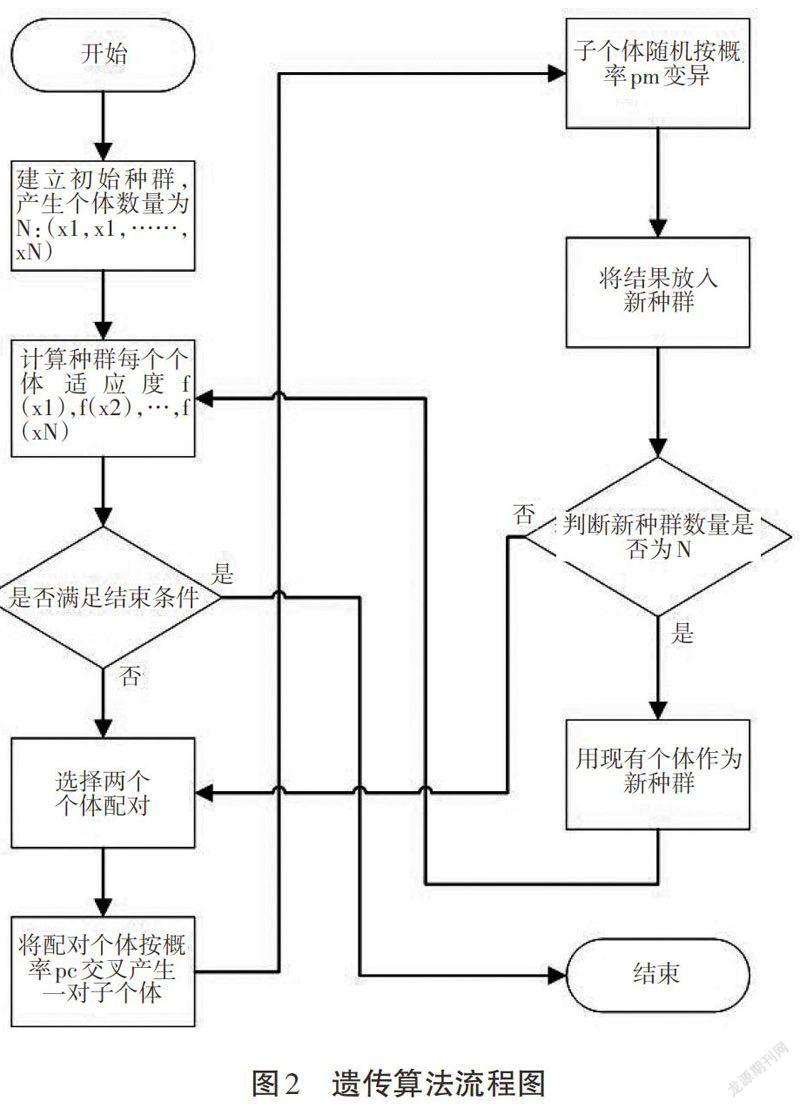
本文将遗传算法用于多节匹配变换器的优化设计，旨在优化各节的特性阻抗。遗传算法流程图见图4。

①要确定的是初始种群和编码方式。种群的规模不易太小，否则计算精度不高，太大则影响效率。对于多节匹配变换器，变换器中某一节特性阻抗[Zn]作为一个个体[xn]中的一个染色体[gn]（[gn∈xn]）；一组变换器特性阻抗的解的集合（[Z1，Z2，…，Zn]）作为一个个体；由N个个体组成的集合即为规模为N的种群（[x1，x2，…，xN]）。经过多次仿真发现，在本问题中，种群规模N=100时比较合适。

②种群中个体的编码可以用二进制编码或实数编码。二进制编码方便简单，但每一代都需要对染色体进行编码和解码，计算时会产生较多额外计算，影响效率；实数编码可以提高最优解精度，加快收敛，减少运行时间。本算法模型采用实数编码。

③遗传算法中适应度函数的作用是模拟生物界适者生存。如果个体适应度低，那么被淘汰的概率就会增加。本文以目标函数作为适应度函数，这种方法适用于模型相对简单的问题。

④遗传算法停止有两种方式：一种是设置算法的最大迭代代数；另一种是设定当个体满足适应度达到某一条件后可以停止。通过多次仿真，代数等于5 000前算法已收敛，所以将这个值作为最大迭代代数maxgen=5 000。在迭代结束后，适应度最高的个体为最优解，在本模型中最优结果是变换器各节的特性阻抗。

4 算法仿真

本文将用二项式响应设计与遗传算法设计的结果用MATLAB做仿真比较，仿真电路如表1所示。

图3到图6为电路1到电路4的设计仿真结果，图形所表现的是反射系数在[θ∈[0，π]]区间的频率表现。

如图3所示，在电路1参数条件下，二项式响应设计要优于遗传算法，但遗传算法也能满足设计目标。

从图4至图6能看出，遗传算法的优化设计明显优于二项式响应，二项式响应的结果并不能完全满足设计目标。

5 结论

本文提出了一种基于遗传算法的宽频匹配电路优化设计方法，通过多组电路设计参数进行设计與仿真，并与二项式响应设计方法进行对比，较好地验证了基于遗传算法的优化设计明显在大失配负载（[ZL/Z0]较大）、大带和多节数下有更优的反射系数，完全达到设计目标，符合设计要求。

参考文献：

[1]王文祥.微波工程技术[M].北京：国防工业出版社，2009.

[2]张肇仪，周乐柱，吴德明.微波工程[M].北京：电子工业出版社，2006.

[3]周明，孙树栋.遗传算法原理及应用[M].北京：国防工业出版社，1999.

[4]康传华，潘明海，贲德，等.基于遗传算法的共形阵列导引头波束综合[J].航空兵器，2013（2）：25-28.