基于CEEMD的小波软阈值和粗糙度惩罚平滑技术的联合信号去噪方法

李薇 白艳萍 王鹏 姚建丽

摘 要：为了有效去除采集信号中的噪声，基于MEMS水听器在采集信号时混入不同噪声的情况下，提出了一种基于CEEMD的小波软阈值和粗糙度惩罚平滑技术的联合信号去噪方法。CEEMD用于将一个含噪信号分解为几个固有模态（IMFS），然后把几个固有模态和原始信号作一个线性相关分析，分为相关性高的模态和相关性低的模态。将软阈值技术应用于相关性低的固有模态，并将粗糙度惩罚平滑技术应用于相关性高的固有模态，以提取尽可能多的信息，然后把处理后的新的固有模态重构形成去噪信号。分别在仿真和真实数据的基础上进行了实验，验证了方法的有效性。结果表明，联合信号去噪方法无论在去噪效果和性能指标上都优于基于CEEMD的小波软阈值的去噪方法和CEEMD的去噪方法，克服了经验模态方法和小波软阈值去噪的不足，为进一步分析与处理信号提供参考。

关键词：噪声与振动控制;CEEMD;IMFS;小波软阈值函数;粗糙度惩罚平滑技术;去噪

中图分类号：TN911   文献标志码：A

Denoising method based on CEEMD combine wavelet

threshold and rough punishment

LI Wei， BAI Yanping， WANG Peng， YAO Jianli

（School of Science， North University of China， Taiyuan， Shanxi 030051， China）

Abstract：In order to denoise effectively during signal collection， and because MEMS hydrophone mixes different noises in signal acquisition， a combined signal de-noising method based on CEEMD soft threshold and roughness penalty is proposed. Signal containing noise by CEEMD method decomposes into several intrinsic mode （IMFS）， and then a linear correlation analysis of intrinsic mode and original signal is conducted. Modals both with high dependency and low dependency are divided. We apply soft threshold technology to low inherent modals， and roughness of punishment is applied to the intrinsic modes of high correlation to extract as much information as possible， The intrinsic mode of denoising is reconstructed to form the new signal.In this paper， the method is used to test on the basis of simulation and real data.In order to verify the effectiveness of the method， experiments were carried out on the basis of simulation and real data respectively.The results show that this method is superior to both ceemd-based wavelet soft threshold de-noising method and CEEMD de-noising method in terms of de-noising effect and performance index. This method overcomes the shortcomings of empirical mode method and wavelet soft threshold denoising， and lays a foundation for further analysis of signal processing.

Keywords：noise vibration control; CEEMD; IMFS; wavelet threshold function; rough punishment technique; denoise

传感器水声微弱信号的提取方法有很多种，经验模态分解法对非线性信号是一种有效可行的去噪方法，虽然此法可以根据信号的特点自适应选择基底对信号进行多分辨率分析，但其分解的固有模态函数（imf）会产生模态混叠的情况[1]。为了降低模态混叠的影响，文献[2]在EMD基础上提出了集合经验模态（EEMD）。在EEMD的基础上，文献[3]提出了互补集合经验模态分解（CEEMD）。CEEMD是将2对相反的白噪声添加到原始信号中，分别进行EMD分解并将结果进行平均而得到最终的imf，该方法进一步减轻了模态混叠问题，同时使分解结果更彻底。研究结果表明，模态分解和阈值技术的结合可以显著提高不相关模态的去噪效果[4]，笔者提出了基于CEEMD的小波软阈值和粗糙度惩罚平滑技术[5]的联合信号去噪方法，

CEEMD用于将一個含噪信号分解为几个固有模态（IMFS），然后把所有固有模态和原始信号做一个线性相关分析，分为相关性低的固有模态和相关性高的固有模态。然后，将软阈值技术应用于相关性低的模态进行去噪，将粗糙度惩罚平滑技术应用于相关性高的模式，以提取尽可能多的信息，处理后的新的固有模态重构形成去噪信号。

1 基于CEEMD的联合去噪方法

1.1 CEEMD算法

CEEMD是以EMD为基础，在EEMD上进行改进的一种算法，包含以下步骤。

1）在原始信号的基础上，加入了n组正负成对的辅助噪声，然后获得2套imf集合：

式中：S表示原始信号;N表示辅助噪声;M1，M2分别表示加入正、负成对噪声后的信号。最后，得到2n个集合信号。

2） 对集合中的每个信号都进行EMD分解，每个信号都可以得到一组imf，将第i个信号的第j个imf分量记作Cij。

3） 将得到的2n組imf进行平均，得到最终的imf分量：

该算法需要添加2个参数：辅助白噪声幅值k和对数N，当N=100时，k取0.01～0.10。

1.2 小波软阈值去噪

1.2 1 小波软阈值处理理论

小波阈值去噪的基本原理是设置一个临界阈值λ，若小波系数小于λ，则系数主要是由噪声产生的，可把这部分系数去掉;若小波系数大于λ，则这些系数主要是信号产生的，可留下这部分系数，然后，利用小波反变换对小波系数进行处理得到去噪后的信号[6]。

1.2 2 阈值的确定

研究中，选取的阈值最好刚好大于噪声的最大水平，可以证明的是噪声的最大限度以非常高的概率低于σ

（此阈值是由Donoho提出的），其中根左边的这个参数就是估计出来的噪声标准方差（根据第1级分解出的小波细节系数），小波系数模按大小排列，然后取最中间值，此值除以0.674 5就得到噪声在某个子带内的方差。

笔者将用此阈值处理各尺度上的细节系数，全局阈值就是近似系数不作任何阈值处理外，其他均作阈值处理。

1.2 3 阈值函数的选取

确定了噪声在小波系数（域）的阈值门限之后，就需要有个阈值函数对这个含有噪声系数的小波系数进行过滤，去除高斯噪声系数，常用的最有效的阈值函数为软阈值函数。

1.3 粗糙度惩罚平滑技术的介绍

由于模态混叠的影响，与原始信号相关的模态仍然含有噪声。然而，这些模态的噪声非常小，不适当的去噪会导致信号失真。粗糙度惩罚平滑技术可以有效地控制去噪信号的平滑度，防止噪声抑制和信号失真的不良影响，因此，对于本研究中的相关模态，可利用粗糙的惩罚技术来平滑，定义如下[7]：

S=∑[DD（]Nn=1[DD）]（fn-f*n）2+λ∫（f*（x）″）2dx，（3）

式中：fn是第n个原始信号元素值;f*n是对应的降噪值;f*（x）表示估计函数;惩罚系数λ是由交叉验证决定的[8]。平方项的总和衡量的是对原始数据的估计函数的拟合度，等式右边的第2项是可以控制估计函数平滑度和避免过度拟合的惩罚项。粗糙度惩罚平滑技术的本质是最小化S并找到f（x）的估计函数，这就使相关模态的可接近性和平滑性达到了平衡。

交叉验证的基本思想是把数据分成2部分，一部分为拟合样本，另一部分为验证样本，首先用拟合样本估计光滑函数，然后再用验证样本来检验光滑拟合效果。

一个选择光滑参数的常用方法是使用交叉验证的极端形式，即对于给定的一个λ，只留一个观测值作为验证样本y*i，用其余观测值估计光滑函数，从而获得该观测值的估计值，如果对每个观测值轮流执行这个程序，可以计算出它们的误差平方和，

VC（λ）=∑ni=1（y*i（λ）-y（i））2，（4）

在λ的某个区间内求解本式的最小值问题即可获得需要的惩罚系数λ。

2 联合去噪方法

2.1 CEEMD去噪

1）将原始信号进行CEEMD分解，然后得到一组固有模态分量。

2）将含噪多的固有模态去掉，一般是第1个固有模态imf1，然后把剩余的固有模态重构形成去噪信号。

2.2 CEEMD与小波软阈值的联合去噪

1）将原始信号进行CEEMD分解，然后得到一组固有模态分量。

设：噪声信号y（t）=x（t）+η（t），式中：x（t）是无噪声信号;η（t）是有限振幅的独立噪声;噪声信号y（t）首先被CEEMD分解为固有模态imf分量。

2） 由于前几层高频imf中仍然含有少量细节信号，所以用小波软阈值函数对前几层imf提取细节信息，得到新的分量，与剩余分量进行重构。选用小波基为db7，小波软阈值函数如下：

[AKc^]i（t）=cni-λni， cni≥λni，

0， |cni|≤λni，

cni+λni， cni≤ -λni，（5）

去噪信号的重组可用下式表示：

[AKx^]（t）=∑[DD（]Ni=1[DD）][AKc^]i（t）+rN（t）。（6）

2.3 基于CEEMD的小波软阈值和粗糙度惩罚平滑技术的联合信号去噪方法

1）将原始信号进行CEEMD分解，然后得到一组固有模态分量。

2） 把固有模态分量与原始信号作线性相关性分析，分为线性相关高的和线性相关低的固有模态。

3）将相关性高的固有模态用粗糙度惩罚平滑技术处理，将相关性低的固有模态用小波软阈值来提取有用的信号，最后，把处理后的模态重构成去噪信号。

3 实验对比

3.1 仿真实验

笔者对所提出的3种算法进行了仿真比较。通过对中北大学国防重点实验室在汾河进行的汾机实测数据的分析研究，能够看出信号为一单频正弦信号序列，而信号在发射和传输的过程中，不仅受到机器本身干扰而产生漂移现象，而且还受到周围环境噪声的影响。因此，笔者选用的仿真实验信号为s（t）=0.1cos（2π·500t），其振幅为0.1，频率为500 Hz，实验所用软件为Matlab。需要向该信号中加入随机噪声、脉冲噪声，使得仿真实验结果更接近实测数据。仿真实验选用信噪比和均方差作为性能指标，信噪比越高、均方差越小性能指标越好，其计算公式如下：

SNR=10lg∑[DD（]Ni=1[DD）]s2i（t）/∑[DD（]Ni=1[DD）][si（t）-s′i（t）]2，（7）

MSE=1N∑[DD（]Ni=1[DD）][si（t）-s′i（t）]2，（8）

式中：si（t）为原始信号数据序列;s′i（t）为去噪后的数据序列;N为信号序列个数。

笔者取去噪前信噪比为1.32 dB的加噪信号进行去噪，图1是含噪信号经过CEEMD方法分解后得到的各层固有模态，可以看出原始信号主要集中在imf2，imf3上，固有模态与原始信号相关性如图2所示。

CEEMD去噪方法是直接去掉第1层固有模态，把剩余模态重构得到去噪信号，然后取其中200～400个点进行放大观察，如图3所示。

CEEMD与小波软阈值的去噪是把前2层模态进行小波软阈值去噪，经过选取不同小波基进行多次试验，小波基函数选取ym8、分解层数为5效果最好，去噪后的模态与剩余的模态重构形成去噪信号，取200～400个点放大，如图4所示。

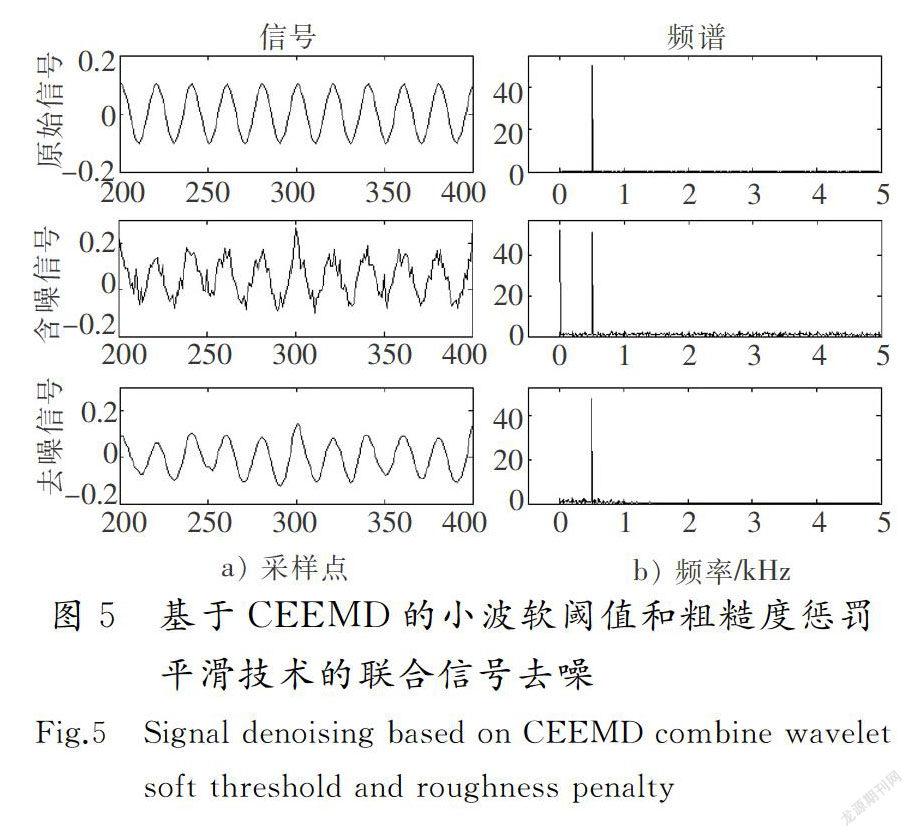
基于CEEMD的小波软阈值和粗糙度惩罚平滑技术的联合信号去噪，是把固有模态和原始信号作相关性分析，结合图1和图2可以看出imf2，imf3与原始信号相关性高，把这2个模态用粗糙度现的，选取100个点做交叉验证，只留1个观测值作为验证样本，其余的99个观测值用于估计光滑函数，从而获得该观测值的估计值，然后计算出误差平方和，求解误差平方和最小化的过程中得出最优惩罚系数λ=5，剩下的模态用小波软阈值去噪，对处理后的模态进行重构，得到去噪信号，取200～400个点放大，如图5所示。

从图5可以看出明显的效果，笔者提出的方法效果较好，仿真选了5组信噪比不同的含噪信号进行仿真去噪，分别得出了用CEEMD分解仿真去噪，基于CEEMD软阈值去噪，基于CEEMD的小波软阈值和粗糙度惩罚平滑技术的联合信号去噪，前后的性能指标。表1是去噪的性能指标对比。

通过对图3、图4、图5和表1的性能指标对比可知，5组试验中基于CEEMD的小波软阈值和粗糙度惩罚平滑技术的联合信号去噪方法的信噪比SNR均比其他方法大，均方差MSE均比其他方法小，得出本文提出的基于CEEMD的小波软阈值和粗糙度惩罚平滑技术的联合信号去噪的效果要好。因为对于线性相关性高的模态的噪声非常小，不适当的去噪会导致信号失真，粗糙惩罚平滑技术可以有效地控制去噪信号的平滑度，防止噪声抑制和信号失真的不良影响。而对于线性相关度低的模态用模态分解和软阈值技术的结合可以显著提高相关度低的模态的去噪效果，这比单独使用小波软阈值去噪提取含噪多的高频模态更有效，由仿真结果可以明显看出该方法对非线性的含噪信号适用，所以本文中提出的去噪方法值得在提取水听器水声微弱信号去噪中使用。

3.2 物理实例实验

中北大学国防重点实验室的研究人员在汾河二库进行MEMS矢量水听器的湖试实验[10]。本次实验采用二元MEMS矢量水听器线阵，并将其固定于船舷的一侧，阵元之间相距0.5 m，置于水下10 m，基阵上有罗经实时检测基阵姿态，并保持基阵水平，每个阵元输出声压和两路振速信号[9]。发射换能器被放置于基阵的90°方位上边，它分别发射了186，270，331，500，800，1 000，1 500 Hz等连续单频信号，采样频率为10 kHz，采集信号时1号水听器为3，4路信号，2号水听器为1，2路信号。

本次实验数据选取2个MEMS水听器采集到的500 Hz数据中的1，2，3，4这4路信号。对500 Hz的4路阵元信号截取87 001～88 000中1 000个点，得出去噪前的4路实测信号如图6所示，根据图6频谱可看出信号中掺杂着高频噪声和低频的一些干扰，在0 Hz频率处明显有干扰，经过多次去噪分析得出该0 Hz干扰造成了原始信号数据整体发生漂移，使得原始信号远离了本身位置，而很多毛刺的出现是由高频信号造成的，所以在仿真时加入了相似的噪声。基于CEEMD的小波软阈值和粗糙度惩罚平滑技术的联合实测去噪结果如图7所示，从图7可以看出该算法在实际去噪方面有很好的效果[11-15]。

4 结 论

MEMS水听器在接收信号时混入噪声，通过用傅里叶变换方法对接收到的信号进行频谱分析，发现原始信号属于单频正余弦信号，而信号在传播过程中受到多种噪声干扰，主要有脉冲噪声、随机噪声、基线漂移，笔者向余弦信号中加入脉冲噪声、高斯噪声、基线漂移，使仿真信号更接近实际信号，然后分别用几种去噪方法进行仿真去噪。通过仿真实验对比CEEMD去噪、CEEMD与小波软阈值联合去噪和本文提出的基于CEEMD的小波閾值和粗糙度惩罚平滑技术的联合去噪这3种去噪方法的性能指标和去噪效果图，得出在仿真实验中基于CEEMD的小波阈值和粗糙度惩罚平滑技术联合去噪的效果要更好。对实测信号数据用该方法进行去噪，结果表明新去噪方法效果很好，值得提倡。

参考文献/References：

[1] 张树标，王柳，饶运章，等.基于EEMD方法的爆破振动信号去噪研究[J].中国钨业，2015，30（4）：15-20.

ZHANG Shubiao， WANG Liu， RAO Yunzhang， et al. De-noising technology for blasting vibration signal based on EEMD method [J]. China Tungsten Industry，2015，30（4）：15-20.

[2] 董文智， 张超. 基于EEMD分解和奇异值差分谱理论的轴承故障诊断研究[J]. 机械强度， 2012， 34（2）：183-189.

DONG Wenzhi， ZHANG Chao. Bearing fault diagnosis method based on eemd and difference spectrum theory of singular value[J]. Journal of Mechanical Strength， 2012， 34（2）：183-189.

[3] 王姣， 李振春， 王德营. 基于CEEMD的地震数据小波阈值去噪方法研究[J]. 石油物探， 2014， 53（2）：164-172.

WANG Jiao， LI Zhenchun， WANG Deying. A method for wavelet threshold denoising of seismic data based on CEEMD [J]. Geophysical Prospecting for Petroleum， 2014， 53（2）：164-172.

[4] YANG Gongliu， LIU Yuanyuan， WANG Yanyong，et al.EMD interval thresholding denoising based on similarity measure to select relevant modes[J].Signal Processing， 2015，109（C）：95-109.

[5] RASTI B， SVEINSSON J R， ULFARSSON M O， et al. Hyperspectral image denoising using first order spectral roughness penalty in wavelet domain[J]. IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing， 2014， 7（6）：2458-2467.

[6] 赫彬， 白艳萍， 张雅婷. 基于不同经验模态分解的小波软阈值ECG去噪研究[J]. 数学的实践与认识， 2016， 46（6）：136-144.

HE Bin， BAI Yanping， ZHANG Yating. A study of wavelet soft threshold of ECG denoising based on different empirical mode decomposition [J]. Mathematics in Practice and Theory， 2016， 46（6）：136-144.

[7] HECKMAN N E，RAMSAY J O.Penalized regression with model-based penalties[J].Canadian Journal Statistics， 2010，28（2）：241-258.

[8] RAMSAY J O， SILVERMAN B W. Functional Data Analysis， Introduction to the Roughness Penalty Approach[M].  New York： Springer-Verlag New York Inc.，1997.

[9] 王鹏.基于MEMS矢量水听器阵列的声目标定向定位技术研究[D].太原：中北大学，2013.

WANG Peng. Research on Acoustic Target Directional Positioning Technology Based on MEMS Vector Hydrophone Array [D]. Taiyuan： North University of China， 2013.

[10]李軍，李青.基于CEEMDAN-排列熵和泄漏积分ESN的中期电力负荷预测研究[J].电机与控制学报，2015，19（8）：70-80.

LI Jun， LI Qing. Medium term electricity load forecasting based on CEEMDAN-permutation entropy and ESN with leaky integrator neurons[J]. Electric Machines and Control， 2015，19（8）：70-80.

[11]CAO Junhong，WEI Zhuobin.Independent component analysis in frequency domain and its application in stractural vibrition signal seperation[J].Procedia Enginering， 2011，16（3）：511-517.

[12]王祁. 传感器信息处理及应用[M]. 北京： 科学出版社， 2012.

[13]孙贵青， 李启虎. 声矢量传感器研究进展[J]. 声学学报， 2004， 29（6）： 481-490.

SUN Guiqing， LI Qihu. Progress of study on acoustic vector sensor[J]. Acta Acustica， 2004， 29（6）： 481-490.

[14]孙淑珍. 基于MEMS的矢量水听器的研究[D]. 哈尔滨：哈尔滨工程大学， 2006.

SUN Shuzhen. Research on Vector Hydrophone Based on MEMS [D]. Harbin： Harbin Engineering University， 2006.

[15]赫彬，白艳萍.基于CEEMDAN小波包的MEMS水听器信号去噪[J].数学的实践与认识， 2016，46（13）： 139-147.