南水北调中线工程分水口敏感性研究

吴怡 郑和震 雷晓辉 王澈

摘要：南水北调中线工程按闸前常水位方式运行，分水口（退水闸）流量变化会引起渠道水位的波动，工程正常运行要求渠道水位下降速率不超过0.15m/h。为了满足这一要求，构建南水北调中线工程一维水力学模型，分析分水口（退水闸）流量变化引起的渠池下节制闸闸前水位的变化过程，进而确定其敏感性。结果表明：同一渠池、同一工况下，不同分水口的敏感性不同；渠道流量越大，分水口的敏感性越小。但是不同渠道流量下的分水口敏感性差异极小，在实际运行中可忽略其影响，用不同渠道流量下的敏感性平均值来最终表征敏感性。

关键词：分水口；敏感性；流量变化；渠道水位；南水北调中线工程

中图分类号：TV122+.5

文献标志码：A

doi： 10.3969/j.issn.1000-1379.2018.07.026

南水北调中线T程总干渠全长1432km，沿线设置64座节制闸、97座分水口和54座退水闸。节制闸是实现渠道运行控制的主要设施，将长距离输水渠道划分为多个渠段，实现对渠道水位和流量的控制；分水口是满足沿线取水需求的主要设施；退水闸是为应对应急工况将渠道水体排出渠道的设施。在实际运行中，通过节制闸的调节控制，将沿线各处需求的水量送达分水口门。输水调度过程中，为保证渠道衬砌不被破坏，工程正常运行要求渠道水位下降速率不能超过0.15m/h和0.30m/d。

20世紀50年代末，国外就提出灌溉系数敏感性分析的研究方法。D.Rrenault等对灌溉渠系的敏感性进行了一系列的分析研究，分析了取水口门流量对渠道水位变化以及操作行为改变的敏感性。文献指出，退水闸和分水口闸门结构类似，出流流量变化会引起渠道水位的波动，这一影响可用敏感性来表征，并分析了分水口流量变化速率、分水变量占渠段流量比例和分水口流量变化幅度这3个参数对敏感性的影响，结果表明敏感性仅由分水口流量变化幅度决定。但是，上述文献的敏感性分析是针对分水口（退水闸）流量变化后，分析分水口（退水闸）断面水位在最初1h内的变化速率。而南水北调中线干线T程以闸前常水位的方式运行，实际调度过程更关注节制闸闸前水位，并且渠道中的水尺当前仅立在节制闸闸前闸后，分水口（退水闸）处没有水位测量，已有研究成果不能完全满足工程实际运行调度管理的需求。

因此，本文构建南水北调中线干线工程一维非恒定流水力学仿真模型，分析分水口流量变化对渠池下节制闸闸前水位的影响，为工程实际运行调度管理提供技术支持。

1数学模型

针对南水北调中线工程特点，构建一维非恒定流水力学仿真模型，对节制闸、分水口、退水闸、渠道等内部构筑物进行概化处理，并与圣维南方程组进行耦合。同时采用稳定性好、计算精度高的Preissmann四点时空偏心格式对方程组进行离散，用高效率的计算方法——双扫描法求解。

总干渠输水线路非恒定流计算采用一维圣维南方程组，由连续性方程和动量方程组成：式中：A、Q为断面面积和流量；x、t为空间和时间坐标；q为单位长度渠道上的侧向人流流量；a为动量修正系数；Z为水位；g为重力加速度；Sf为水力坡度；S0为渠道底坡坡度。式中：K为流量模数。

节制闸为弧形闸门，其流态可分为堰流和闸孔出

流。判断标准为式中：e为闸门开度；H0为包括行进流速在内的闸（堰）前水头。

堰流公式为

2敏感性分析

为分析分水口（退水闸）流量变化对所在渠段下节制闸闸前水位的影响，选取中线T程前3个渠池的分水口、退水闸为研究对象（表1），以第1个渠池（陶岔渠首闸一刁河节制闸）的肖楼分水口为例，介绍敏感性指标求解过程。

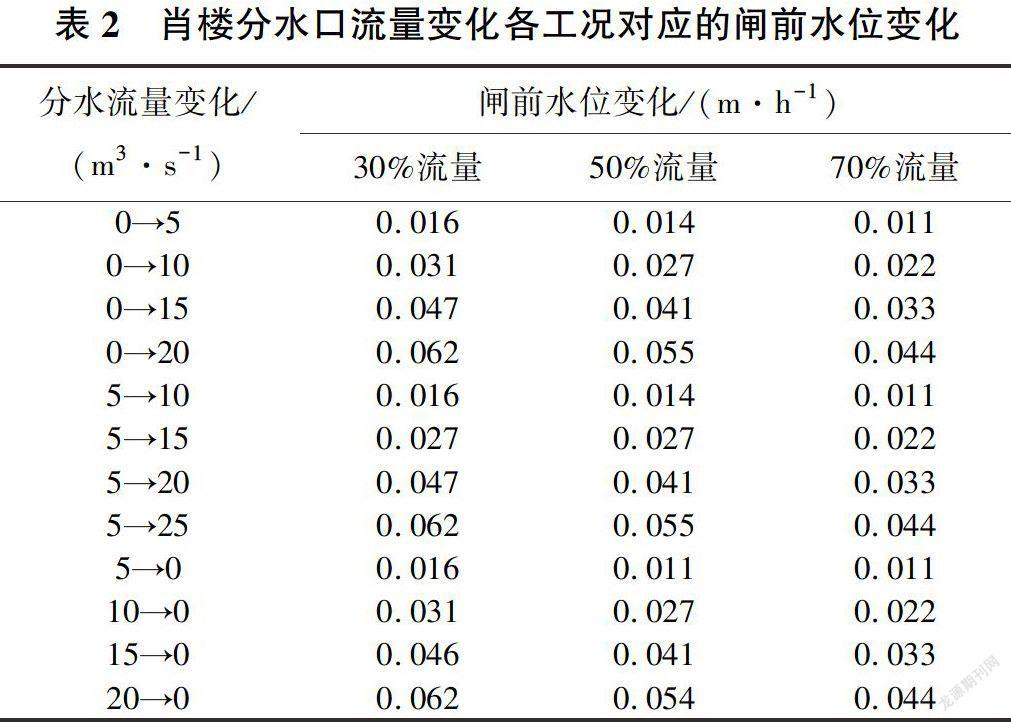
由于文献已证明敏感性仅与分水口流量变化幅度相关，因此仅分析分水口流量变化幅度这一参数。渠池初始状态假设为3种状态——节制闸闸前水位为设计水位，渠池流量分别为设计流量的30%、50%和70%；模型计算步长为600s；假设各种流量变化均在600s完成。刁河节制闸闸前水位在最初1h的变化情况见表2。由表2可知，同一工况下，即使肖楼分水口分水流量变化的初值和末值不同，只要变化幅度相同，刁河节制闸水位变化就相同，分析结果见表3。

对表3数据整理后进行曲线拟合，得到分水口流量变化幅度与闸前水位变化速率关系曲线，见图1。式中：y为闸前水位变化速率；x为分水口流量的变化幅度。

文献中渠道敏感性指标公式为式中：S为基于闸前水位的敏感性指标；△H为最初1h的闸前水位变化速率；△Q为分水口流量的变化幅度。

因此，敏感性指标为分水口流量变化幅度与闸前水位变化速率关系曲线的斜率。由此可确定渠段流量为设计流量的30%、50%和70%情况下的敏感性指标分别为0.0031、0.0027和0.0022。而由闸前水位下降速率平均值求出的敏感性为0.0027，因为各分水流量变化幅度下闸前水位下降速率的标准差极小，因此0.0027即为肖楼分水口的敏感性指标。

采用上述方法，可分别求出刁河退水闸、望城岗分水口、湍河退水闸、彭家分水口、严陵河退水闸在3种工况下的敏感性指标，进而由平均值可确定其敏感性指标，计算结果见表4。通过敏感性指标可知，为满足渠道水位下降速率不超过0.15m/h的要求，肖楼分水口、刁河退水闸、望城岗分水口、湍河退水闸、彭家分水口、严陵河退水闸的流量变化幅度（AQ=0.15/5）分别不应超过55.6、51.7、78.9、46.9、46.9、45.5m^3/s。

由表4可见，同一工况下，敏感性关系为肖楼分水口<刁河退水闸，望城岗分水口<湍河退水闸，彭家分水口<严陵河退水闸，因此同一渠池、同一工况下，不同的分水口（退水闸）的敏感性不同，越靠近下节制闸敏感性指标越大。肖楼分水口、刁河退水闸、望城岗分水口、湍河退水闸、彭家分水口和严陵河退水闸在渠池流量占设计流量的30%、50%和70%的条件下，敏感性递减，因此渠道流量越大，分水口（退水闸）的敏感性指标越小，但是差异极小。

通过分析可知，敏感性指标是分水口流量变幅和渠池流量变化这两个影响因素共同作用的结果。但是同一工况下，分水口流量变幅引起的闸前水位变化比渠道流量变化更为敏感，即分水口流量变幅是影响渠道水位的主要因素。尤其对于南水北调中线工程渠道而言，同一工况下，不同渠道流量对闸前水位变化的影响仅为毫米级，在实际运行中可忽略其影响。因此，分水口（退水闸）的敏感性可以用其在不同渠池流量下的敏感性指标的平均值来表征。

3结语

本文构建了南水北调中线工程的一维非恒定流数值模拟模型，研究了节制闸闸前水位变化对分水口（退水闸）流量变化的敏感性，并应用到前3个渠池的分水口和退水闸进行分析。结果表明：同一渠池中，在同一工况下，不同的分水口（退水闸）的敏感性不同；渠道流量越大，分水口（退水闸）的敏感性越小，但差异极小。分水口流量变化幅度是敏感性的主导因素，渠道流量对敏感性的影响极小，可用不同渠道流量下的敏感性平均值来最终表征敏感性，进而可计算分水口流量变幅的阈值。