重构背景值双变权GM （1，1）中长期预测模型构建

王彤 张凯 杨军 刘瑞 张浩祥 周晓 涂杰

摘要：为了解决传统GM（1，1）模型在中长期预测中存在的局限性和较大偏差问题，提高模型预测精度，拓宽其应用范围，结合全信息变权弱化缓冲算子、全信息加权平均法、Newton-Cotes公式和三次牛頓插值公式，从原始数据变换、背景值重构、初始条件优化3个方面对传统GM（1，1）模型进行改进，建立了重构背景值双变权 GM（1，1）中长期预测模型。用西安市年供水量统计数据对模型进行精度检验与分析，结果表明精度检验等级为一级，具有很好的预测精度，可用于西安市年供水量的预测。

关键词：GM（1，1）模型：变权弱化缓冲算子；加权平均法；中长期预测模型

中图分类号：TV213.4

文献标志码：A

doi： 10.3969/j.issn.1000-1379.2018.07.011

精确预测城市需水量是相关部门合理制定供水规划的前提。城市水资源供需关系是一个多因素、多层次、多目标的复杂系统，包含许多未知和不确定的影响因素，难以具体明确这些影响因素与供水量之间的函数关系。运用灰色系统理论，避开城市水资源供需复杂关系的影响因素，以年供水量时间序列为基础，通过建立灰色GM（1，1）模型来揭示城市年供水量变化规律是一种有效途径。

在进行中长期预测时，数据的波动性和随机性较大，传统GM（1，1）模型存在不同程度的局限性和较大偏差。近年来，国内外众多学者从原始数据的处理、累加生成方法的改进、初始值优化、背景值优化、模型参数估计、残差优化、综合优化等方面对传统GM（1，1）模型进行了深入研究，同时，GM（1，1）模型在模糊回归和区间灰数预测方面的拓展成为研究的热点。笔者根据传统GM（1，1）模型的建模机理，通过引入全信息变权弱化缓冲算子，结合全信息加权平均法、Newton -Cotes公式和三次牛顿插值公式，从原始数据变换、背景值重构、初始条件优化3个方面对传统GM（1，1）模型进行改进，建立了重构背景值双变权GM（1，1）中长期预测模型，并用西安市年供水量统计数据进行验证，结果表明新建模型具有很好的预测精度。

1改进的GM （1，1）模型建模过程

1.1原始数据变换

原始序列的光滑度对模型预测的精度有一定影响。为降低原始序列的波动性和随机性，改善其光滑性，提高模型预测精度，需要对原始序列x^（0）（k）[x^（0）（k）≥0；k=l，2，…，n]进行数据变换处理。目前，数据变换处理方法主要有函数变换法和构造缓冲算子两大类。变换处理后的新序列应满足级比信息变权弱化缓冲算子对原始序列进行数据变换处理。

无论x^（0）（k为单调递减序列、单调递增序列，还是波动序列，定义d为全信息变权弱化缓冲算子，有：式中：A为变权缓冲系数，A∈（0，1）；y^（0）（k）为全信息变权弱化后的缓冲序列。

1.2背景值重构

传统GM（1，1）模型的背景值采用梯形公式（即n=1时的Newton-Cotes公式）求解，其误差较大，精度较低。文献先后提出了基于插值法和New-ton-Cotes公式的组合法来构造背景值。

由于n=4时的Newton-Cotes公式具有5次代数精度，精度明显高于具有1次代数精度的梯形公式，且牛顿插值公式计算过程较拉格朗日插值公式简单，因此本文在已有文献的基础上，采用基于n=4时的Newton-Cotes公式和牛顿插值公式的组合法来构造背景值。

首先，采用n=4时的Newton-Cotes公式得出背景值Z^（1）（k+1）为

将式（3）代人式（2），求得背景值Z^（1）（k+l）（k=1，2，…，n-3）：将式（6）代人式（5），解得Z^（1）（k）（k=n-1，n）为

综上，基于n=4时的Newton-Cotes公式和三次牛顿插值公式组合法的背景值重构公式为

1.3初始条件优化

在上述原始数据变换的基础上，将y^（0）（k）的一阶累加序列x^（1）（k）（k=1，2，…，n）中各数据的加权平均值作为优化后的初始条件：

x^（1）（t）=αlx^（1）（1）+α2x^（1）（2）+…+αnx^（1）（n）（9）

结合新信息优先原则，新数据比旧数据赋予更大权重，即满足αl<α2<…<αn。

权重αk为

基于全信息加权平均法的初始条件，将新信息的重要程度通过较大权重充分体现，同时考虑了旧信息的作用，是一种直观优化初始条件的新方法。

1.4重构背景值双变权GM（1，1）中长期预测模型的建立步骤

（1）设x^（1）（k）≥0（k=l，2，…，n）为原始序列，由式（1）对其进行数据变换，得到经全信息变权弱化后的缓冲序列y^（0）（k）。

（5）结合式（9），得出改进的GM（1，1）模型的时间响应式为式中：γ为时间参数

2精度评估

灰色预测模型的精度通常采用均方差比值C、小误差概率P和关联度K共同检验。式中：e^（0）k）为残差，e为残差均值；S1为残差的标准差；_S2为x^（0）（k）的标准差；x为x^（0）（k）的均值。

关联度K计算公式为

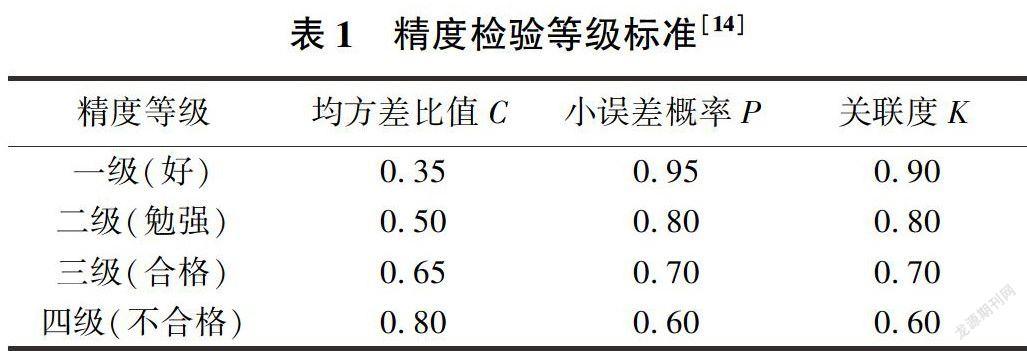
均方差比值C越小、小误差概率P越大、关联度K越大，则精度越高。精度检验等级标准见表1。

3应用实例

表2为西安市2000-2016年年供水量统计数据，据此绘制年供水量变化曲线（见图1）。可以看出，数据整体随机性强，为波动序列。2006年西安市年供水量呈下降趋势，原因可能是城市产业结构调整及阶梯水价的实施，促使居民节水意识增强，从而用水量略有下降。但随着城市居民生活水平的提高和工业现代化的高速发展，西安市年供水量总体呈上升趋势。

3.1模型计算

以西安市2000-2016年年供水量数据为原始序列x^（0）（k），计算级比σ^（0）（i），可知不满足σ（i）∈（0.894 8，1.1175），故采用全信息变权弱化算子对x^（0）（k）进行处理，在误差最小化目标下得出最优变权缓冲系数A=0.39，从而得到缓冲序列y^（0）（k）。采用上述的步骤（1）～步骤（5），建立年供水量预测模型，得到时间响应函数为x^（1）（k）= 39038 288.71e^{（0.001 49（k-11.602 87））}-38363 231.61

（22）

由式（17）进行一阶累减还原，得到預测结果x^（0）（k）。具体预测结果及误差见表3，实际数据与预测结果比较见图2。

3.2精度检验及分析

对模型进行精度检验，得均方差比值C=0. 008 836，小误差概率P=l，关联度K=0.9956。结合表1精度检验标准可知，模型预测精度为一级，预测结果精度高。从表3可得预测值的平均相对误差为0.53%。从图2可看出，拟合效果好，具有很好的参考价值。同时，预测模型时间响应函数中-a=0.00149<0.3，满足GM（1，1）模型进行中长期预测的条件要求，故重构背景值的双变权GM（1，1）中长期预测模型可用于西安市年供水量数据的预测。

4结语

通过对传统GM（1，1）模型建模机理的研究，本文在3个方面对模型进行了改进：①引入全信息变权弱化缓冲算子d对原始数据进行变换处理，使其满足级比σ（i）要求，降低数据随机性，增强数据平滑度；②推导n=4时的Newton-Cotes公式和三次牛顿插值公式的组合公式来重构背景值，以增强模型进行中长期预测的稳定性；③利用新信息优先原则，通过全信息加权平均法优化初始条件。在此基础上建立重构背景值的双变权GM（1，1）中长期预测模型，经实例分析验证，得出以下结论和建议。

（1）所建新模型克服了传统GM（1，1）模型难以进行数据中长期预测的不足，模型对西安市2000-2016年年供水量数据进行预测验证，预测值的平均相对误差为0.53%，精度后验差和关联度检验结果均为一级，模型预测精度高、拟合效果好，可用于西安市年供水量的预测。

（2）根据模型预测结果，供水企业可结合城市现状自来水厂综合供水能力，合理制定近远期供水规划。同时，相关部门可结合自来水厂改扩建或新建项目，合理调控水厂生产能力，使有限的水资源发挥更大的效益，以满足城市用水需求，与城市总体发展规划相协调。