连铸结晶器非正弦振动装置建模与固有特性分析

周 超 张兴中 刘平飞 关 杰

1.燕山大学国家冷轧板带装备及工艺工程技术研究中心，秦皇岛，066004

2.河北农业大学海洋学院，秦皇岛，066003

3.中国重型机械研究院有限公司，西安，710032

0 引言

结晶器非正弦振动在提高拉坯速度、有效地避免黏结性漏钢、提高铸坯质量等方面效果明显，因此研究结晶器非正弦振动对实现高效连铸具有重要的意义［1］。

结晶器非正弦振动的核心是振动装置，目前工业上应用的结晶器振动驱动装置主要有3种：液压驱动系统、伺服电动缸驱动系统和机械驱动装置。液压驱动系统能够方便地实现任意振动波形及参数的在线调整，但系统比较复杂，且投资及维护费用较高［2］。伺服电动缸驱动装置由镭目公司开发［3］，可以实现振幅、频率和波形偏斜率的在线调节，但伺服电机频繁的正反转影响位移、速度等的跟踪精度以及系统响应速度，同时，滚珠丝杠的承载能力难以与液压装置及曲柄机构相媲美。PARK等［4］将偏心轴部分做成凸轮轮廓，零件一旦制造出来，波形、振幅和波形偏斜率都不能调节，且三角形、矩形波等速度突变较大的波形都不能实现。机械驱动装置结构简单、成本低、便于维护、可靠性好。张兴中等［5］开发的椭圆形齿轮驱动结晶器非正弦振动装置具有良好的工艺特性和动力学特性，但齿轮啮合时的齿侧间隙产生啮合冲击和噪声，齿轮的偏心质量引起装置运动不平稳。ZHANG等［6］开发的逆平行四连杆驱动结晶器非正弦振动装置产生波形的原理与椭圆齿轮相同，虽可避免齿轮啮合带来的冲击和噪声，但机构的传动链依然很长。张兴中等［7］开发的双偏心驱动结晶器非正弦振动装置的振动频率在线可调，振幅停机可调，结构简单、加工容易、投资少，但对加工精度要求较高。与液压驱动系统相比，上述机械式驱动装置的波形偏斜率都不能在线调节。

为克服上述装置的缺点，本文设计出一种双伺服电机驱动的结晶器非正弦振动装置，其频率和波形偏斜率在线可调，振幅停机可调，能够很好地使结晶器实现非正弦振动。与正弦振动相比，非正弦振动虽有良好的工艺特性，但运动的平稳性较差，因此，对非正弦振动系统的动力学研究有重要意义。本文对双伺服电机驱动结晶器非正弦振动装置进行研究，重点研究装置固有特性的变化规律。

1 非正弦振动装置

1.1 振动系统工作原理

双伺服电机驱动结晶器非正弦振动系统主要由驱动装置、缓冲弹簧、导向板簧、结晶器及振动台等组成，如图1所示。由于系统左右对称，故取一半模型，其工作原理如图2所示。工作时，伺服电机驱动减速器，减速器通过联轴器连接偏心轴，通过电机变角速度运动，使偏心轴带动连杆在S点的铅垂方向上产生非正弦振动。在缓冲弹簧和导向板簧的作用下，连杆推动振动台及其上的结晶器上下振动。

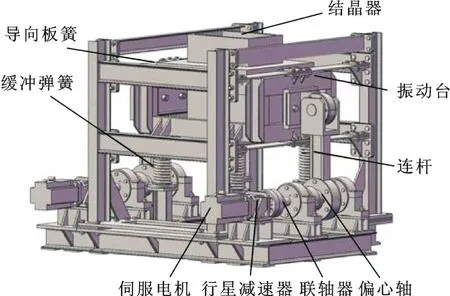
图1 双伺服电机同步驱动结晶器非正弦振动装置Fig.1 Non”sinusoidaloscillator synch ronously d riven by double servomotors

1.2 运动学分析

德马克非正弦振动波形的位移曲线表达式为［8］

式中，h为振幅，mm；f为振动频率，Hz；A为波形偏斜因子；t为时间，s。

图2 非正弦振动系统工作原理Fig.2 W orking p rincip le diagram of non”sinusoidal oscillation system

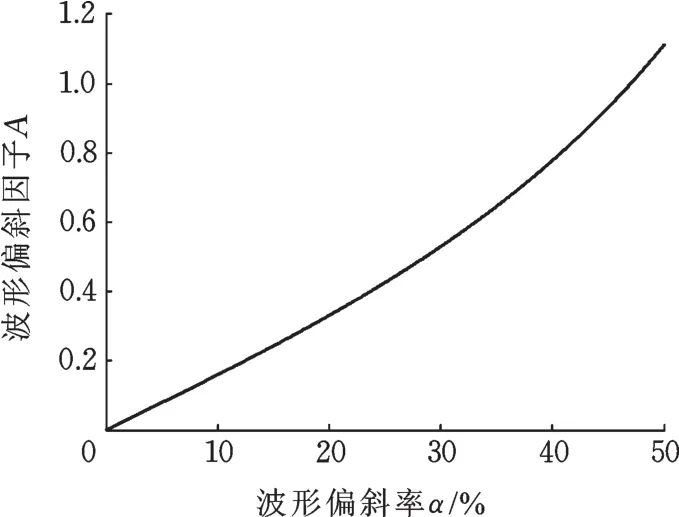
如图3所示，在一个振动周期内，非正弦振动波形的峰值滞后于正弦波形的峰值，可以推导出波形偏斜因子A和波形偏斜率α的关系。当s=h时，可得到位移峰值时间tc与A的关系：

h=h sin(2πftc-A sin(2πftc)) （2）

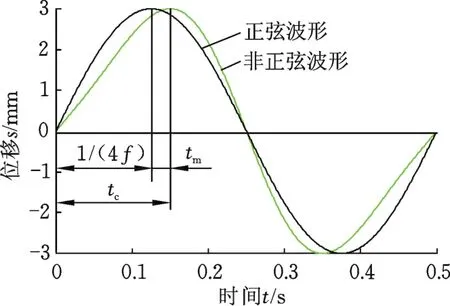
图3 非正弦与正弦振动位移波形Fig.3 Disp lacem en twaveform of non”sinusoidal and sinusoidal oscillation

所以在一个振动周期［0，1/f］内，存在

解得

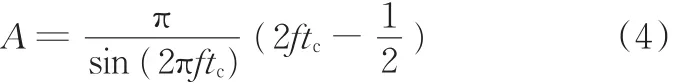
滞后时间

波形偏斜率

α =4f tm（6）

联立式（5）、式（6）得

将式（7）代入式（4）解得

波形偏斜因子A和波形偏斜率α之间的关系见图4。

在铅垂方向上，连杆运动的位移与结晶器振动的位移一致，由二者的位移关系可得偏心轴角速度的表达式：

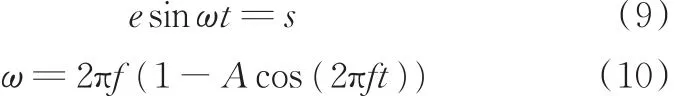
式中，ω为偏心轴的角速度，rad/s；e为偏心轴的偏心距，mm。

图5给出了不同波形偏斜率下偏心轴的角速度曲线。只要偏心轴按某一特定的规律旋转，即可实现德马克非正弦振动波形。

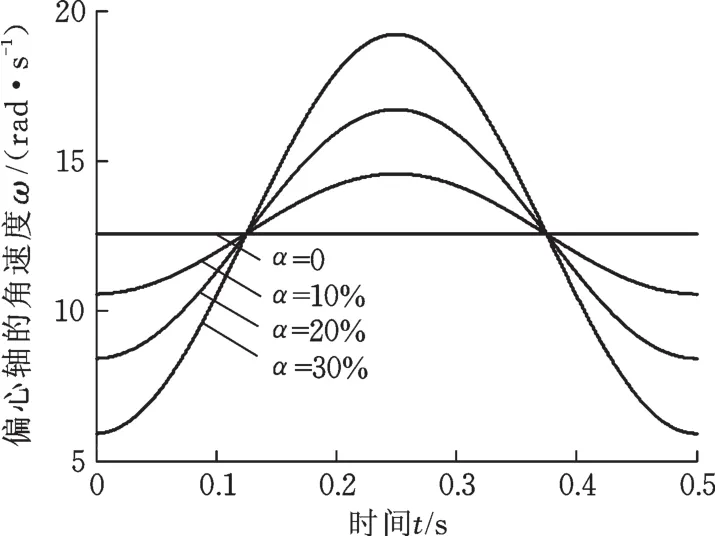
图5 不同波形偏斜率下偏心轴角速度Fig.5 Eccen tric shaft angu lar velocity of d ifferent waveform deviation factors

由图1建立非正弦振动装置的刚柔耦合三维模型，取α=20%，f=2 Hz，h=5 mm，对装置进行运动学仿真，得到德马克非正弦振动波形，如图6所示，从而验证原理的正确性。

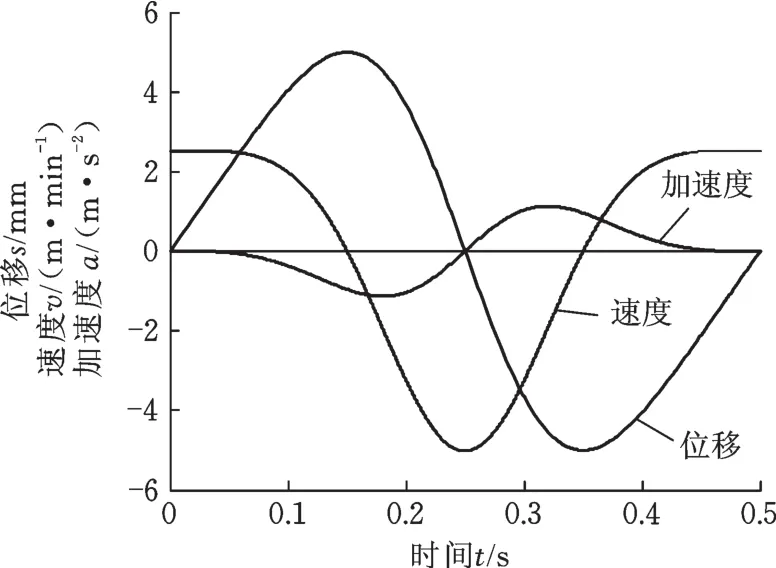
图6 机构振动波形曲线Fig.6 Oscillation waveform ofm echanism

2 系统动力学模型的建立

根据非正弦振动系统中各构件的受力和变形特点，忽略曲柄、连杆、齿轮的弹性变形及运动部件间的间隙和摩擦，认为伺服电机运转平稳可靠。伺服电机驱动结晶器非正弦振动系统动力学模型（图7）是扭振和线振耦合模型，该模型把实际位移分解为静态位移和弹性位移［9］。

图7 非正弦振动系统动力学模型Fig.7 Dynam icmodel of non”sinusoidal oscillation system

图7中，T0为伺服电机输出转矩；J0为伺服电机输出轴的转动惯量；θ0为伺服电机输出轴的角位移；kθi为扭转刚度，i=1，2；k1、k2分别为连杆上下两部分的抗压刚度；ci为联轴器阻尼系数；θj为转动部件静态角位移，j=1，2，3；Δθj为转动部件弹性角位移；m1为连杆的质量；y1、y2分别为连杆及结晶器纵向的静态位移；Δy1、Δy2分别为连杆及结晶器纵向的弹性位移；k3e为弹簧的弹性刚度；k4e为板簧的弹性刚度；m2为结晶器及振动台的质量；Ffe为铸坯与结晶器之间的摩擦力；J1、J2、J3分别为减速器的主动齿轮、从动齿轮及偏心轴的转动惯量。

选取Δθ1、Δθ3、Δy1、Δy2为独立广义坐标，其他广义坐标由所选取的广义坐标来表示。由偏心轴的转角与连杆纵向位移之间的关系可得

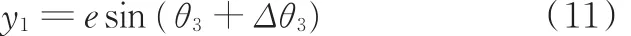
将式（11）展开得

偏心轴的转角很小时，cosΔθ3≈ 1，sinΔθ3≈ Δθ3。代入式（12）得到

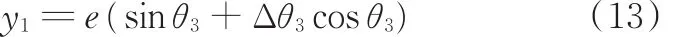
由于连杆与结晶器振动台在铅锤方向上的运动位移相同，故有y1=y2。

由非正弦振动系统各部件之间的运动学关系，可得各部件静态位移之间的关系：θ0=θ1，θ2=θ3，y1=y2。

假设减速器为刚体，齿轮不变形，则减速器传动比为

3 振动系统微分方程的建立

根据图7建立的动力学模型及第2节中各参数之间的关系，采用带阻尼的拉格朗日方程：

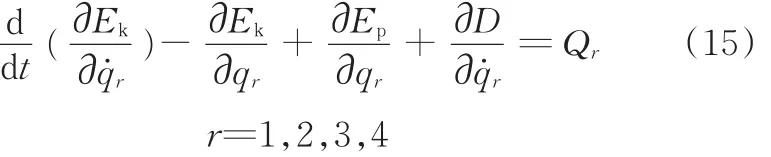
式中，Ek为振动系统的动能，J；Ep为振动系统的势能，J；Qr为系统的广义激振力，N；D为系统的广义阻尼力，N；qr为系统的广义坐标。

推导出该系统的运动微分方程。

根据系统的动力学模型和各部件运动参数之间的关系得到系统的动能、势能及阻尼项：

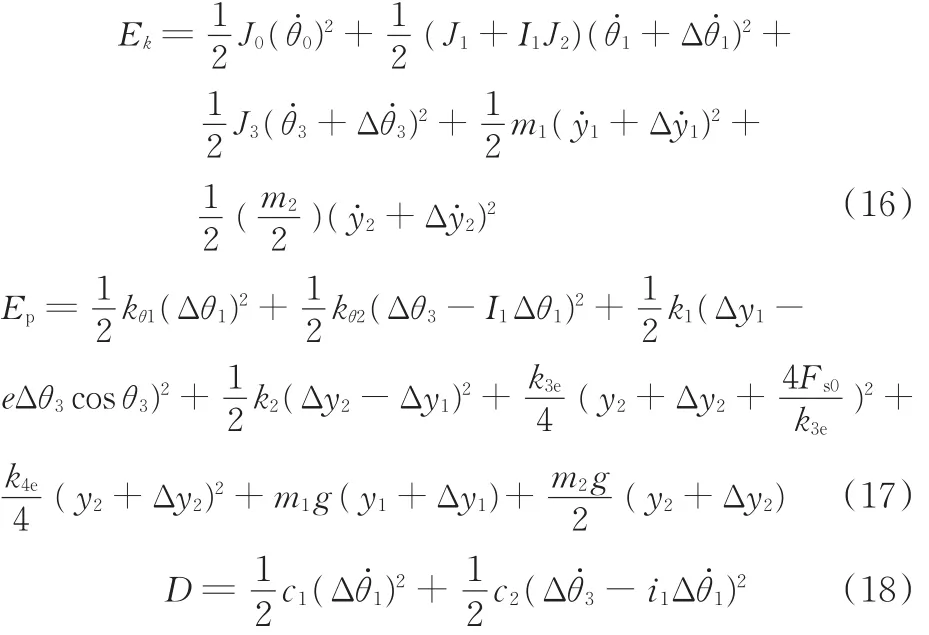
将式（16）～式（18）代入系统的微分方程式（15），得到系统受迫振动微分方程：

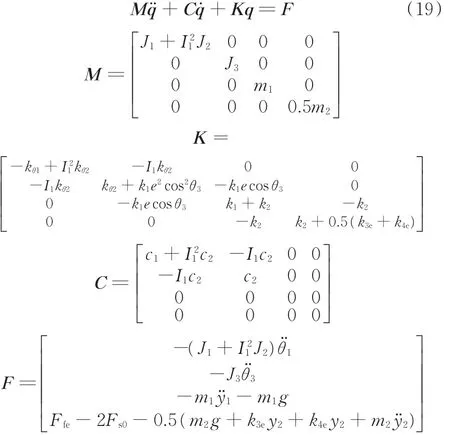
式中，M为质量矩阵；K为刚度矩阵；C为阻尼矩阵；F为广义力向量；g为重力加速度，m/s2；Fs0为缓冲弹簧预紧力，N；q 为位移向量，q=(Δθ1,Δθ3,Δy1,Δy2)T；q˙为速度 向 量 ，q˙=(Δθ˙1,Δθ˙3,Δy˙1,Δy˙2)T；q¨为 加 速 度 向 量 ，q¨=(Δθ¨1,Δθ¨3,Δy¨1, Δy¨2)T。

由动力学参数之间的关系可知，伺服电机驱动结晶器非正弦振动系统的质量矩阵为常量，刚度矩阵、阻尼矩阵和激励矢量都是随时间周期变化的。

4 动力学分析

线性定常系统可采用多刚体系统动力学方法来求解其特征值和特征向量。双伺服电机驱动结晶器非正弦振动装置为周期时变参数系统［10⁃11］，可通过瞬时机构凝固法求解其固有频率。将转角θ3在某一瞬间凝固，则系统的刚度矩阵变为常系数矩阵，采用结构动力学的方法来计算系统的固有频率。计算所需系统的特征参数见表1。

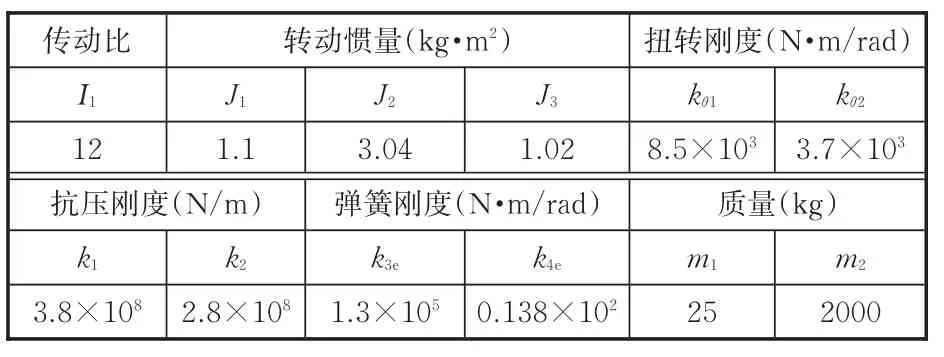
表1 系统的特征参数Tab.1 Characteristic parameters of the system

4.1 非正弦振动系统固有频率

将式（19）转变为如下的无阻尼自由振动系统：

即

式中，ωj为振动系统的固有角频率，rad/s；fj为振动系统的固有频率，Hz；φj为振动系统的特征向量。

本文采用瞬时机构凝固法对式（21）进行编程求解，得到系统的固有频率。由非正弦振动系统动力学模型可知，固有频率为偏心轴的转角及振幅的函数，与结晶器振动的频率及波形偏斜率无关。

4.1.1 偏心轴的转角和振幅对固有频率的影响

由图8可以看出，系统的固有频率是周期时变的，振幅较小时，各阶固有频率的波幅并不大，且随振幅的增大，波幅变大。由于系统的固有频率不受频率和波形偏斜率的影响，因此调节频率和波形偏斜率，可避免固有频率的变化，扩大了参数的选取范围，更有利于实现结晶器的最佳振动模式。

4.1.2 系统惯性参数对固有频率的影响

对于非正弦振动系统，当结晶器振幅h=5 mm时，只改变各构件的惯性参数，其他参数保持不变，系统的固有频率也将发生变化。以系统1阶固有频率为例进行说明。由图9a可以看出，减速器的主动齿轮、从动齿轮的转动惯量及连杆的质量对非正弦振动系统的固有频率影响较小；结晶器及振动台质量减小时，固有频率略有增大。由图9b可以看出，偏心轴的转动惯量减半后，系统的固有频率增加幅度较大，若要提高系统的固有频率，只需适当减小偏心轴的转动惯量。结晶器振动频率远离系统的固有频率，有利于高效连铸。

图8 系统的固有频率Fig.8 Natu ral frequency of the system

4.1.3 构件的刚度对固有频率的影响

由图10可以看出，偏心轴的刚度对系统的固有频率改变较大，其他参数对固有频率影响很小。

4.2 系统的振型

图11给出了装置的前3阶振型，可以看出，系统的各阶振型同固有频率一样，也是周期变化的，且在系统的传动部分，振型变化较为剧烈。因此应增大传动系统轴的刚度，减小传动系统的转动惯量，以提高系统固有频率，降低传动系统的波动。

图9 固有频率与系统惯性参数的关系Fig.9 Relationship between natu ral frequency andinertia param eters of the system

图10 构件刚度减半后系统固有频率Fig.10 Natural frequency of the system w ithcom ponent stiffness halved

5 结论

（1）设计出一种新型双伺服电机驱动结晶器非正弦振动装置，该装置可以实现波形偏斜率和频率的在线调节、振幅的停机可调。

（2）采用集中参数法建立了双伺服电机驱动结晶器非正弦振动系统动力学模型及动力学方程。分析表明，固有频率是周期时变参数，且不受结晶器振动频率及波形偏斜率的影响，因此参数的选择范围扩大了，更有利于实现结晶器的最佳振动。

（3）偏心轴的转角、惯性参数、刚度对系统的固有频率影响较大，而其他参数影响较小；由振型显示可得传动部分的刚度对固有频率影响较大。

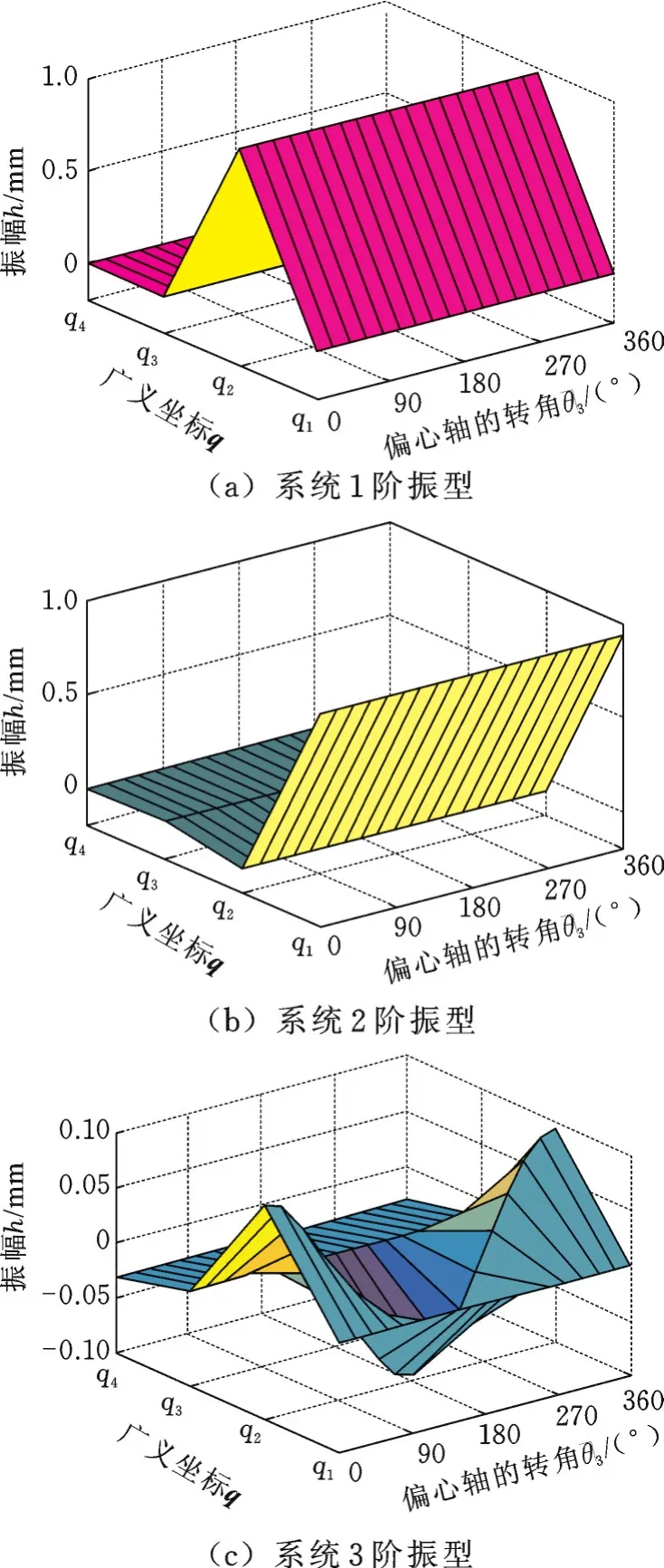
图11 系统的振型Fig.11 System m ode shape