基于改进限幅法的变换域通信峰均比抑制算法

尚 影，时鹏飞

（1.阜阳幼儿师范高等专科学校 科学与健康系，安徽 阜阳236015；2.中国电子科技集团公司第十四研究所，江苏 南京210013）

作为一种认知抗干扰通信技术，变换域通信（transform domain communication，TDC）利用电磁环境中实时感知的空闲频谱信息，通过多载波调制构造与干扰正交的波形，实现了频谱聚合通信。但这种基于频谱感知的设计使得TDC波形具有较高的峰均比（peak to average power ratio，PAPR），既不利于信号的低检测性能，也会损失前端功率放大器的效率，进而限制通信传输距离。目前，源于传统正交频分复用（orthogonal frequency division multiplexing，OFDM）系统的PAPR抑制算法可以降低高PAPR信号对TDC性能的影响。

限幅类算法是通过利用窗函数对时域信号的超过设定门限的峰值进行幅度限制[1]，是一种最简单的PAPR抑制方法。但该类方法对信号进行非线性处理，这会带来严重的带内失真和带外干扰。TDC的时域基函数是建立在频谱正交的基础上，时域限幅会导致带外干扰会影响其他通信信道的通信性能，带内失真会导致TDC通信比特误码率的损失。为此，Jean等人提出了限幅滤波法（clipping filter，CF）有效地解决了带外干扰问题[2]。针对限幅滤波法带来的带内失真，Chen等人提出了噪声消除算法，从频域的角度预测限幅噪声[3-4]。然而，这些基于时域限幅的改进算法并不能完全解决对TDC造成的非线性失真问题。为此，本文提出了无失真的限幅调制方法，并且在解调端不会产生信噪比损失。

1 变换域通信及其峰均比

发射端通过宽带频谱感知、生成频谱幅度序列、随机相位调制和逆快速傅里叶变换（inverse fast fourier transform，IFFT）等几个过程后得到TDC的时域基函数序列，然后通过循环码移键控（cyclic code shift keying,CCSK）调制构造最终的发射波形，而接收端通过频谱感知生成本地的相关序列用于相关的CCSK解调。

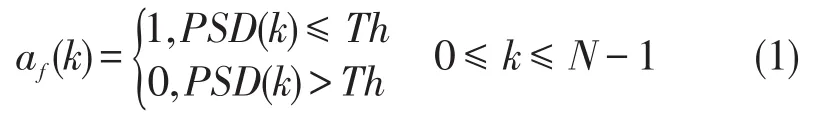
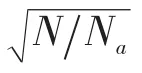
其中j是复数单位。通过IFFT将频域基函数B变换为时域基函数b=[b(0),…,b(n),…,b(N-1)]T，其中b(n)表示为：

图1 传统TDC的整体系统流程图

由于TDC的发射信号是利用CCSK循环移位来携带信息，其发射信号的PAPR和原始的基函数b=[b(0),…,b(n),…,b(N-1)]T的 PAPR 是一致的，因而TDC信号的峰均比定义为基信号b的峰值功率与平均功率的比值：

其中，E(·)表示 TDC 信号的平均功率，max(·)为TDC信号的最大功率，N是TDC信号的长度。此时，基于可用频点数Na的TDC信号的峰值功率表示为：

根据帕萨瓦尔能量守恒准则[6]，TDC信号的平均功率为：

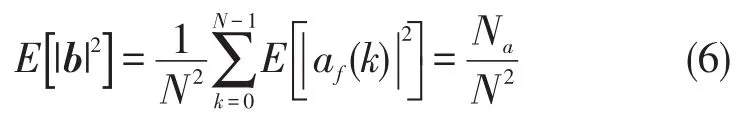
将式（5）和式（6）代入到式（4）中，则TDC信号的PAPR表示为：

由式（7）可知，在信号长度N一定的条件下，随着可用频点数目Na的增加，PAPR的最大值出现的概率也随之增加。原始TDC的高PAPR导致带内频谱扩展、与干扰正交性遭到破坏和比特误码率增加等不利影响，限制了TDC的通信传输距离，因此需要对TDC的PAPR进行抑制。

2 基于改进限幅法的峰均比抑制算法

其中 |b(n) |是b(n)的幅度，φk是b(n)的相位，A0是限幅门限值定义为[7]：

其中CR是限幅率（单位：dB），σ是信号功率的均方根，定义为：

由式（9）和（10）可知，当信号的功率一定时，CR越大，限幅门限A就越高。反之，限幅门限A0越低。

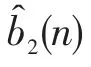
3 性能分析

图2 基于不同限幅率设计的TDC信号

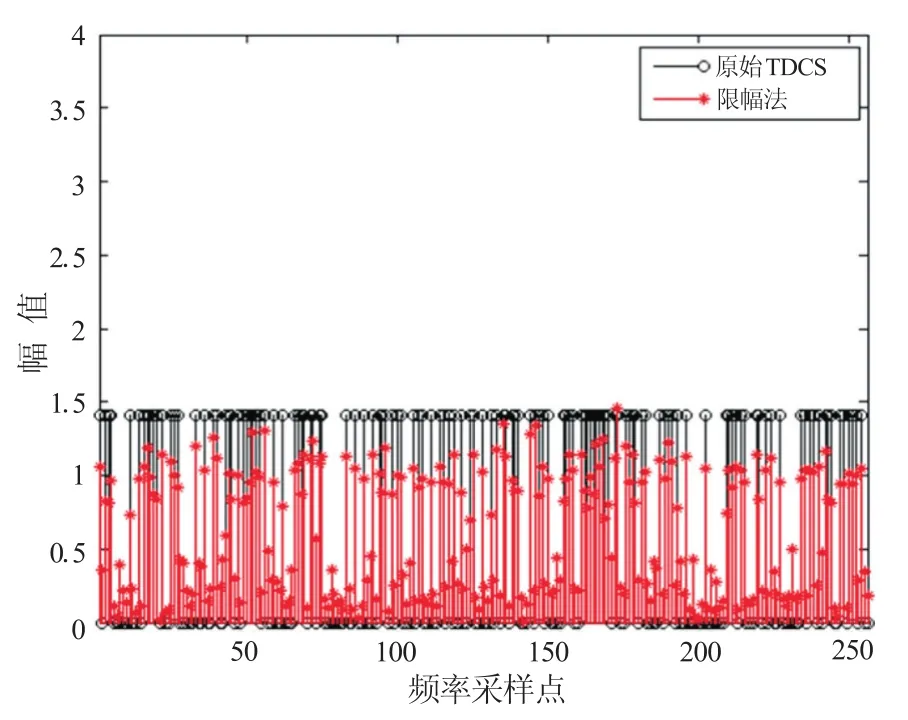
图3 限幅后的TDC信号频谱分布

图4 基于改进限幅法的TDC信号PAPR及比特误码率

4 小结

本文针对传统基于时域限幅算法导致的TDC造成的非线性失真问题，提出了无失真的限幅调制方法。该方法通过多次限幅调制和变换域频谱幅度矩阵相乘的方式产生低峰均比的波形，并在接收端采用该波形进行匹配接收，进而在降低峰均比的同时不产生信噪比损失。