定向钢纤维增强水泥基复合材料抗拉细观模拟

卿龙邦， 喻渴来， 慕 儒， 葛志明

(河北工业大学 土木与交通学院， 天津 300401)

在水泥基体中掺入适量的钢纤维，能有效阻碍基体微裂缝的衍生和发展，显著提高水泥基体的抗裂能力[1-6]及抗冲击能力[7-8].在普通钢纤维增强水泥基复合材料(SFRC)中，只有少部分钢纤维与基体主拉应力方向一致，钢纤维的阻裂增韧效率较低.在隧道管片、路面、轨枕等特定的结构中，对钢纤维进行定向，使钢纤维排列方向与受拉方向一致或者接近，则能有效提高钢纤维的增强和阻裂效率.Abrishambaf等[9-11]利用自密实混凝土在成型过程中钢纤维的分布近似旋转垂直于混凝土流动方向这一现象，制备了钢纤维环形分布的自密实混凝土板，研究了钢纤维分布方向对混凝土力学性能及断裂性能的影响.慕儒等[12-13]利用钢纤维在磁场中的磁化特性，制备了定向钢纤维增强水泥基复合材料(ASFRC)，开展了劈裂抗拉、抗折及断裂试验[14]，研究表明：定向钢纤维增强水泥基复合材料的抗裂及弯曲性能均优于普通钢纤维增强水泥基复合材料.

采用细观数值方法有利于深入揭示钢纤维水泥基复合材料的破坏机理.Qin等[15]利用递推公式生成随机数，研究了三维钢纤维混凝土生成算法，开展了钢纤维混凝土在爆炸冲击动载作用下的损伤破坏研究.刘丰[16]模拟了普通钢纤维混凝土在静载条件下的损伤破坏过程，未考虑钢纤维与混凝土之间的黏结滑移作用.Rena等[17]在确定梁跨中截面纤维分布规律的基础上，通过将不同角度钢纤维的荷载-滑移曲线换算为等效钢纤维本构关系，对普通钢纤维增强水泥基复合材料在冲击荷载作用下的三点弯曲梁断裂试验进行模拟.Soetens等[18]研究了模型截面钢纤维的角度分布规律，基于弥散裂缝模型研究了端勾型钢纤维对钢纤维增强水泥基复合材料起裂后力学性能的影响.相比于损伤和弥散裂缝模型，基于Belytschko等[19]、Moes等[20]提出的扩展有限单元法能直观反映基体裂缝的产生和发展过程，Ren等[21]考虑钢纤维与混凝土的黏结滑移作用，基于扩展有限元法，开展了钢纤维混凝土多尺度断裂破坏模拟研究.

本文采用随机数生成算法建立了定向钢纤维水泥砂浆细观数值模型，考虑钢纤维与砂浆基体的黏结滑移作用，基于扩展有限元法，开展了不同钢纤维掺量(体积分数，本文所涉及的掺量、含量等均为体积分数，特别说明除外)的定向钢纤维增强水泥基复合材料受拉断裂全过程的模拟研究，并与试验结果进行了对比分析.

1 模型生成

如图1所示，钢纤维在空间中随机分布且互不相交，其位置的随机性主要由钢纤维的中点坐标o(x,y,z)，钢纤维与z轴夹角β，钢纤维的投影与x轴的夹角α控制.

图1 钢纤维空间位置Fig.1 Space position of steel fiber

利用随机数表征钢纤维的中点坐标及其与坐标轴的夹角α和β.为避免钢纤维掺量过高时钢纤维中点坐标和夹角出现重复，采用混合同余法生成随机数，其表达式如下[15,22]：

xn+1=(λxn+c)(modM)

(1)

式中：λ为乘子；c为增量；M为模数；mod为求模算子.

钢纤维投放区域为100mm×100mm×360mm的长方体，为避免边界附近的钢纤维含量较低，选取100mm×100mm×300mm范围内的钢纤维建立数值模型.钢纤维采用圆直型，直径D=0.5mm，长度Lf=30mm.确定钢纤维的投放数量N：

(2)

式中：φsteel为钢纤维掺量；V为试件体积.

逐根投放钢纤维，对超出边界以及彼此相交的钢纤维予以删除，直到所投钢纤维掺量达到要求.图2给出了不同钢纤维掺量的投放结果.

图2 普通钢纤维增强水泥基复合材料数值模型Fig.2 Numerical model of SFRC

在定向钢纤维增强水泥基复合材料中，纤维方向与试件的主应力方向一致[23].基于普通钢纤维增强水泥基复合材料投放算法，建立定向钢纤维增强水泥基复合材料细观数值模型，尺寸为100mm×100mm×300mm(如图3所示).

图3 定向钢纤维增强水泥基复合材料细观数值模型Fig.3 Meso-scale numerical model of ASFRC

2 数值模拟

2.1 基体本构关系

钢纤维混凝土直接拉伸试验难度较大，要求加载仪器有较大刚度，若试件尺寸较大，将难以获得稳定的破坏过程.近年来国内外关于钢纤维混凝土直拉试验的研究均采用小尺寸试件，在Abrishambaf等[24]的定向钢纤维水泥基复合材料直拉试验中，试件受拉部分的尺寸为30mm×40mm×134mm.Hassan等[25]的钢纤维增强水泥基复合材料直拉试验试件截面尺寸为50mm×50mm，试件高度不超过200mm.JG/T 472—2015《钢纤维混凝土》规范中规定试件的最小边长不应小于钢纤维长度的2.5倍.本文掺杂的钢纤维长30mm(具体参数见表1)，试件尺寸为100mm×100mm×400mm.现有试验机上下两个夹头之间的净高减去夹具的长度和荷载传感器的长度，使得试件的长度不超过400mm，本文采用黏钢法进行单轴拉伸试验，为保证试件与钢板夹具的黏贴效果，经后期切割后的试件实际尺寸为100mm×100mm×300mm.

表1 钢纤维特征参数

砂浆的水灰比(质量比)为0.32，配合比见表2.采用P·O 42.5普通硅酸盐水泥；标准砂的细度模数为2.6；减水剂采用减水率18%(质量分数)的聚羧酸型；每种纤维掺量试件浇筑3组，按文献[13]所述方法制备定向钢纤维水泥砂浆试件，其制备过程如下：(1)将钢纤维与水泥砂浆搅拌均匀，浇筑至非金属模具中；(2)将钢纤维水泥砂浆拌和物置于设置了匀强磁场装置的振动台上(如图4所示)；(3)启动振动台,此时拌和物处于流体状态，基体中的钢纤维在磁场作用下旋转至与磁场方向一致或接近，以此达到定向目的.

表2 水泥砂浆配合比

图4 混凝土中钢纤维进行定向的匀强磁场试验装置Fig.4 Experimental set up for aligning steel fibers in concrete with a uniform magnetic field[13]

采用虚拟裂缝模型[26]描述水泥砂浆基体的拉伸断裂特性.在断裂过程区(FPZ)，虚拟裂缝面上分布着非均匀黏聚力(如图5所示).采用线性的黏聚裂纹型本构关系(如图6所示)，其中Gf为断裂能，ft是基体强度，随着裂缝张开位移ω的增大，裂缝面上的黏聚力σ逐渐减小，当裂缝张开位移ω达到极值ωs时，形成宏观开裂区.

Application of improved ant colony algorithm in optimization design of sewage pipe network

图5 虚拟裂缝模型Fig.5 Fictitious crack model

图6 水泥砂浆本构关系Fig.6 Constitutive of cement mortar

2.2 钢纤维与基体的黏结滑移本构关系

将钢纤维与砂浆基体的黏结滑移作用等效为钢纤维的拉伸作用，其本构关系通过钢纤维拉拔试验得到的荷载-滑移关系曲线换算得到[17-18,21].钢纤维的截面应力σf[17]：

(3)

式中：P为钢纤维拉拔荷载.

钢纤维的应变εf[17]：

(4)

式中：Sf为钢纤维滑移长度.

通过开展单根钢纤维拉拔试验，可有效了解钢纤维与水泥砂浆基体的黏结滑移作用机理，试件为100mm×100mm×100mm的立方体(如图7所示)，水泥砂浆配合比同表2.纤维嵌入长度为20mm，钢纤维拉拔试验结果如图8所示.开展有限元模拟分析时，采用理论荷载-滑移关系曲线(如图8所示).

图7 钢纤维拉拔试件Fig.7 Pull-out test specimen

图8 钢纤维的荷载-滑移关系曲线Fig.8 Pull-out curves for steel fibers

2.3 数值模拟结果

建立2种钢纤维掺量(φsteel=1.2%，φsteel=2.0%)的定向钢纤维增强水泥基复合材料有限元模型，模型所含钢纤维数量分别为6111，10186 根；为避免荷载直接施加于模型两端造成应力集中，在模型两端施加垫块，尺寸为100mm×100mm×30mm；采用8节点实体等参单元对模型进行网格剖分，砂浆基体单元尺寸为5mm，加载板单元最大尺寸为10mm，如图9所示.钢纤维采用2节点杆单元，将划分好网格的钢纤维嵌入砂浆基体中，各相材料力学参数如表3所示.基于扩展有限元法，采用位移加载方式模拟单轴拉伸作用下定向钢纤维增强水泥基复合材料的断裂破坏全过程.

图9 ASFRC有限元模型Fig.9 Finite element model of ASFRC (size:mm)

MaterialElastic modulus/GPaPoissons ratioTensile strength/MPaFracture energy/(N·m-1)Cement mortar300.2 3.2148Steel fiber2100.31150.0

图10 ASFRC的拉伸应力-应变全曲线Fig.10 Tensile stress-strain curves of ASFRC

φsteel=1.2%φsteel=2.0%SimulationTestSimulationTest4.804.447.206.93

对钢纤维进行定向，使其分布方向与试件的主拉应力方向一致或接近，可显著提高钢纤维水泥砂浆的抗拉强度和韧性(如图11所示)，钢纤维掺量2.0%的普通钢纤维水泥砂浆(SFRC)抗拉强度平均值为4.41MPa，相同钢纤维掺量的定向钢纤维水泥砂浆(ASFRC)抗拉强度平均值为6.93MPa,钢纤维定向后的试件抗拉强度提高了57.14%.

图11 SFRC和ASFRC的拉伸应力-应变全曲线Fig.11 Tensile stress-strain curves of SFRC and ASFRC(φsteel=2.0%)

定向后的钢纤维水泥砂浆试件的截面纤维含量显著提高，钢纤维与砂浆基体的黏结滑移作用增强，钢纤维脱黏拔出过程主要发生在全曲线的软化下降段，此时水泥砂浆基体已经开裂，裂缝处的砂浆基体不再承受拉伸荷载，由钢纤维与砂浆基体的黏结滑移抵抗外荷载作用，定向后的钢纤维相比普通乱向钢纤维可显著提高水泥砂浆基体起裂后的韧性.

图12给出了钢纤维掺量为2.0%的模型在单轴拉伸作用下的最大主应力云图.相比普通试验，采用细观数值模型，可有效研究钢纤维的增强作用过程.从图12可看出定向钢纤维增强水泥基复合材料在单轴拉伸作用下呈现多裂缝扩展破坏(如图12(a)所示)，这与试验观察到的结果吻合(如图13所示).当拉伸应力达到基体的抗拉强度时，基体开始产生裂缝，随着外荷载的不断增大，裂缝处的砂浆基体逐渐退出工作，由钢纤维抵抗主拉应力作用；随着裂缝张开位移增大，钢纤维承担的拉应力逐渐增加，砂浆基体虽已失效，但试件仍可承受拉应力作用，且主要由主裂缝处的钢纤维承载(如图12(b)所示)；随着外荷载的增大，微裂缝不断扩展，主裂缝处的钢纤维最终拔出，试件失去承载能力，沿着主裂缝破坏.

图12 ASFRC的最大主应力云图Fig.12 Maximum principal stress nephogram of ASFRC

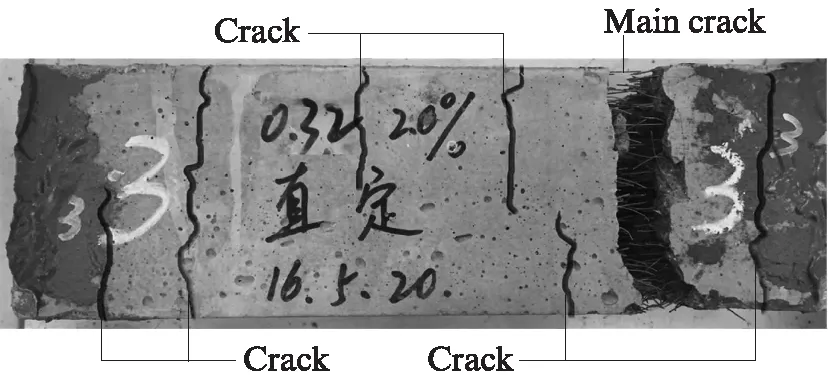
图13 拉伸破坏图Fig.13 Uniaxial tensile failure

图14给出了不同加载时刻定向钢纤维增强水泥基复合材料模型内部最大主应变云图.在加载初期基体主应变较小，砂浆基体还未开裂，当外荷载达到70%Pmax左右时，基体沿着主拉应力方向(x轴)出现裂缝(如图14(c)所示)，随着基体主应变增大，基体主拉应力达到峰值时已形成多条裂缝(如图14(d)所示)，基体进入软化阶段，此时由裂缝处的钢纤维与基体的黏结滑移发挥主要承载作用.

图14 模型内部不同加载时刻的最大主应变云图Fig.14 Maximum principal strain nephogram of model at different loading moments

3 结论

(1)细观模拟得到的拉伸应力-应变全曲线与试验结果吻合较好，在全曲线软化阶段，砂浆基体失去承载能力，由钢纤维与砂浆基体的黏结滑移作用抵抗外加荷载.主裂缝处的定向钢纤维承担主要的拉应力作用，从而显著提高了水泥砂浆起裂后的韧性.

(2)模拟得到定向钢纤维增强水泥基复合材料在单轴拉伸作用下呈现多裂缝扩展破坏，细观模型的破坏结果与试验结果较为吻合.当外荷载达到抗拉强度Pmax的70%左右时，基体开始产生裂缝.由于钢纤维与砂浆基体的黏结作用，当基体承受的外加荷载继续增加时，裂缝附近的基体出现开裂扩展.进入软化阶段，随着钢纤维的拔出，试件逐渐丧失承载能力，沿着主裂缝破坏.