神奇的四数之和

◎ 文、图︱孙守全（业余魔术师）

现象：

表演者在一张纸上画好4行4纵的格子，然后写上数（见图1），请一位观众任意从这16个数中随便选一个数圈掉，然后划掉和这个数同一行及同一列的各数，如果观众圈出6，应该将5、7、8及2、10、14都划去（见图2）。这轮完毕，再请观众在剩下的九个数中任意圈掉一个，划去和它同一行及同一列的各数（见图2），如果观众圈出9，应该将11、12及1、13都划去，这轮完毕，请观众再从剩下的四个数中圈划一次，最后只剩下一个数了，将它也圈起来，如第3轮观众圈出16，应划去15，4，最后剩的3也圈起（见图2）。表演者把圈划的方法教给观众后，就让他们重新去选择进行圈划，表演者不用看最终图上圈的是哪4个数，但是他仍可快速猜出这4个数的总和必定是“34”。

说明：

这个魔术巧妙利用了加法交换律，在我们的圈划规则下，观众圈出的4个数将不在同行同列，用图3示意，在图3表格的顶上写上1、2、3、4，边上写上0、4、8、12，图中每格数字的填写，要将它所在列中的顶上数和所在行中边上数加起来，比如打了圈的那一格在第三列，顶上是3，边上是8，这个格就应该填3加8等于11。按此规则将16个格子都填满就是图1，于是你就可以发现，无论观众最终圈出哪四个数，这四个数都是用顶上和边上的数加在一起后稍加交换，总可以写出（1+2+3+4）+（0+4+8+12）这种形式，而这个式子总等于34。所以数不变的情况下，这个魔术只能变一次。

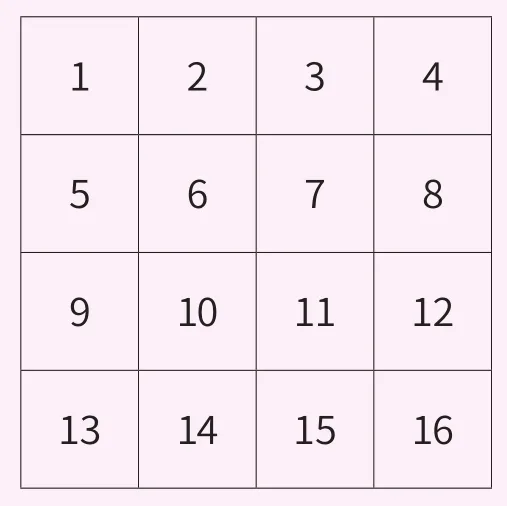
图1

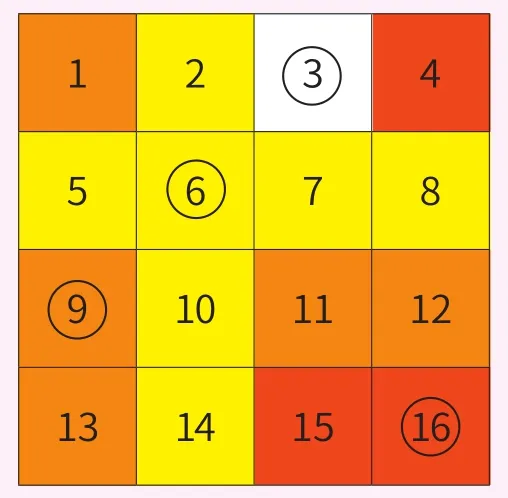
图2

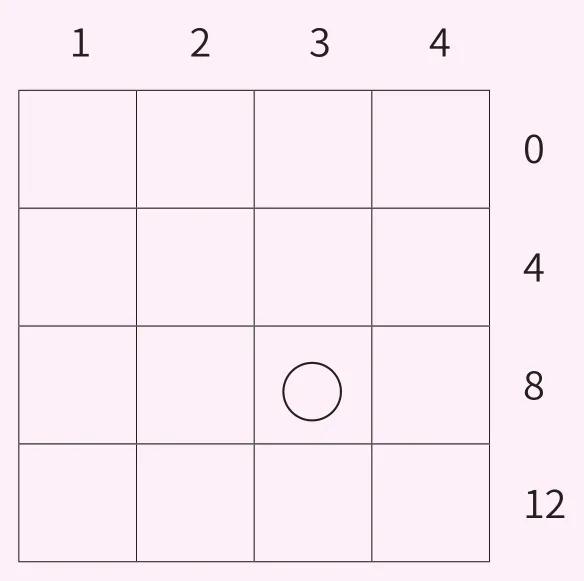
图3

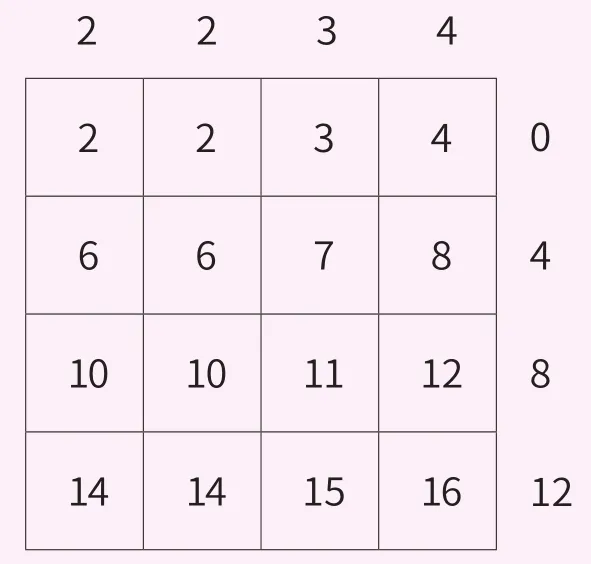
图4

如果变第二次，办法即为改画图1，比如将第一行第一纵第一个顶数由1改为2，将出现图4的情形，而这一次四数相加的和将不再是34，而是35。

按上述方法，你能自造很多图，先用铅笔在顶上和边上各写4个数，按对应相加的方法将16个格子填满，再把顶上和边上的数字擦掉，即可表演新的本节目，你甚至可在外面的8个数中加上几个负数，数字中有正有负，结果就更多样了。■