托卡马克边界局域模的初步模拟研究

吴彦斌

（安庆师范大学科研处，安徽安庆246133）

寻找环保清洁、储量丰富的新能源是整个世界共同面对的问题。核聚变就是把两个轻的原子核聚合成一个较重的原子核，然后释放出能量。与核裂变相比，核聚变具有反应产生的能量更高、反应的产物无放射性污染、主要原料储量更丰富等优点，因此核聚变受到众多国家的广泛关注，被认为是解决能源问题的最佳方法。

托卡马克是一种环形磁约束聚变装置。20世纪50年代，苏联库尔恰托夫研究所最早开展了托卡马克实验研究。经过半个多世纪的探索，托卡马克已经成为受控热核聚变最有可能成功的装置。在托卡马克实验中，等离子体约束一般分为3种状态，即欧姆模式、低约束模式（L模）和高约束模式（H模）。1981年，在德国ASDEX装置上得到了H模的实验结果[1]，等离子体的约束时间比L模预期的高了一倍。H模的简单描述是：在对真空室壁进行处理以后，当加热功率达到某个临界值，发现约束比L模有很大的提高。这类改善约束的主要特征是边界区的反常输运有了大幅度减小，因而边界等离子体的密度和温度都比L模时的约束有了很大提高，形成较陡的密度和温度梯度垒。

H模等离子体在边界具有一个陡峭的压强剖面，压强和自洽产生的自举电流会使边界处产生不稳定性。如果这个不稳定性足够强就会引发边界局域模（ELM），它会把约束区内的热等离子体从边界以丝状的形式抛洒到偏滤器靶板和第一壁上，这种能量对靶板的损害是致命的。因此了解ELM的结构以及特性对于未来聚变反应堆非常重要。

ELM物理机制非常复杂，通常采用数值模拟的方法来研究，BOUT++程序就是其中之一。它由原始的边界流体程序BOUT发展而来，已与一些主流的边界磁流体力学（MHD）程序（ELITE，GATO）校准过。它模拟了台基的崩塌，得到的线性增长率以及模式结构的结果都与之前ELITE程序的结果非常吻合，而抗磁效应、电阻效应和电子粘滞等非线性效应对不稳定性增长率的影响，则是本文主要解决的问题。

1 ELM的基本物理图像和特征

等离子体放电从L模转换为H模，加热功率需大于触发L-H模转换的功率阈值[2]。在从L模转换到H模的放电过程中，等离子体边界区的反常输运被抑制，在磁分界面内侧形成边界输运垒，边界等离子体参数（如密度、温度）空间分布的梯度增大，从而形成等离子体台基（Pedestal），如图1所示。

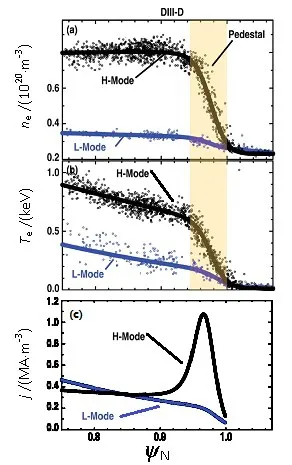
图1 DIII-D装置上典型的H模和L模密度(a)、温度(b)和电流密度(c)剖面

台基区等离子体压强梯度很大，由此产生的自举电流为表面模或气球模的不稳定性增长提供能量，这些MHD扰动激发了ELM，使边界等离子体的压强梯度不能超过一个极限值。

ELM一般表现为多个间歇的瞬时边界能量和粒子损失[3]，其MHD不稳定性的本质使得边界磁面破裂，造成大量的能量与粒子脱离磁约束而作用到边界和器壁，对边界的再循环以及器壁的热负荷造成影响。虽然ELM利于控制等离子体密度和排出杂质粒子从而实现H模放电的稳态运行，但是ELM爆发携带的大量粒子和能量会对装置的第一壁材料造成很大的损坏。

从实验现象上来说，ELM的爆发在偏滤器Dα辐射信号上表现最为明显，边界输运垒的瞬时破裂造成的粒子和能量损失使Dα信号瞬间增强，出现一系列尖峰，并伴随着储能下降和边界台基梯度变平。之后台基继续积累，直到触发下一次ELM。从高速CCD诊断可以看出，ELM具有丝状的空间结构[4]，如图2所示。

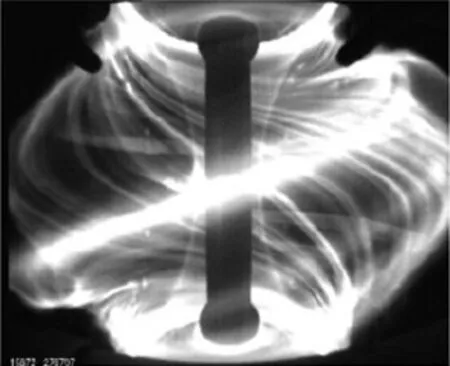
图2 MAST装置上的ELM丝状结构（可见光成像）

ELM爆发的物理机制尚未完全理解。目前广泛认可的理论认为ELM是由剥裂—气球模（peeling-ballooning mode）所激发产生[5]，其中剥裂模由平行电流密度梯度驱动，气球模由压强梯度驱动。

2 BOUT++程序简介

BOUT++由美国劳伦斯•利弗莫尔国家实验室（LLNL），英国约克（York）大学以及其他合作伙伴（包括中国科学院等离子体物理研究所、核工业西南物理研究院、北京大学）共同开发，它是由C++语言写成，使用真实具体的托卡马克的位型，包含三维边界条件，用双流体架构描述边界湍流的模拟程序[6]。

最简单的3场（压强，电流，磁通）剥裂—气球模型包含了抗磁漂移，E×B漂移，电阻率和电子粘滞等非理想物理效应。具体方程如下[7]：

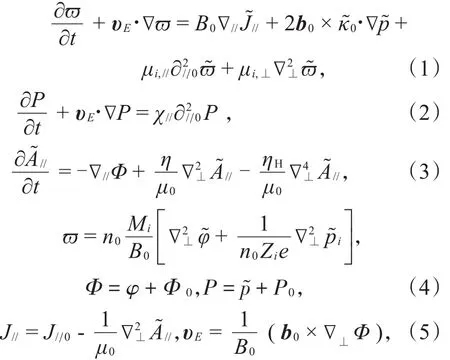
这里υE是E×B漂移速度，Φ是电势，J//是平行电流，B0是平衡磁场。∇//F=B∂//(F/B)中的F是任意的，b0·∇，κ0=b0·∇b0。虽然超电阻ηH，即电子粘滞在碰撞等离子体中可以被忽略，但是在碰撞率较低的等离子体中，它的作用是非常明显的。在这个模型中，理想MHD中的不稳定源来自电阻率或者电子粘滞。

3 模拟结果与分析

求解方程（1）～（5）使用的是场向坐标系，如图3所示。定义如下：

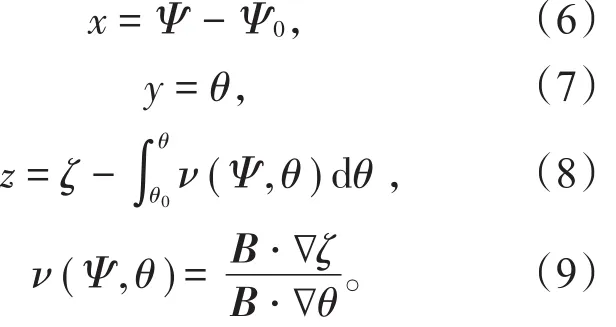
图3 场向坐标系

在BOUT++的3场模型中，对径向（x）的微分需要转换到磁面坐标系，然后再转回场向坐标系。插分方法用的是4阶中央插分以及3阶WENO平流插分方法。

为了研究剥裂—气球模的动力学过程，选择使用TOQ平衡程序[8]生成的圆截面环形平衡（cbm18_dens8），平衡位型如图4所示。模拟的参数如下：小半径a=1.2 m，大半径R0=3.4 m，磁轴上环向磁场强度B0=2 T。BOUT++三场模型，是按照剥裂—气球模型优化的，即研究ELM的最简模型。因此只要有ELM产生，就可以从这个模型中解出不稳定性的增长率。

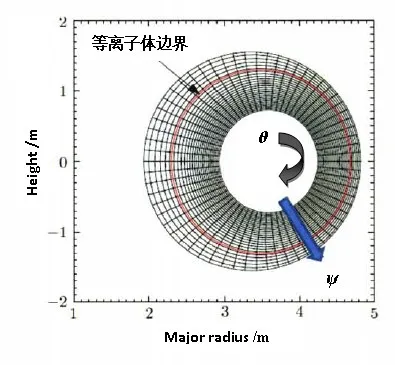
图4 TOQ程序生成的圆截面位型

图5 为抗磁效应对不稳定性增长率的影响。从图中可以看出，理想情况（无抗磁）下，不稳定性增长率随环向模数的增大而逐渐增加；而添加了抗磁效应后，增长率在环向模数较小时缓慢增加，当n≥15时，增长率开始减小，直至n=40时减小为0。这说明抗磁效应抑制了不稳定性的增长，即抗磁效应对于剥裂—气球模有致稳作用，这与理论预测一致[9]。

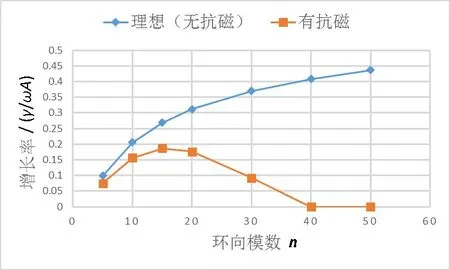
图5 抗磁效应对不稳定性的影响

接下来探讨剥裂—气球模不稳定性与无量纲参数S以及SH的关系。S=μ0R0vA/η，称为Lundguist数，是阿尔芬波横越磁场时标与磁场的电阻性扩散时标之比，其中vA是阿尔芬速度，η是电阻率。类似的，SH= μ0R30vA/ηH，称为超Lundguist数，是阿尔芬波横越磁场时标与超电阻性电流扩散时标之比。图6是加入了电阻效应对不稳定性的影响。与图5比较可得，加入电阻效应之后，不稳定性增长率整体有所增加，这说明电阻会增加剥裂—气球模的不稳定性，形成阻性剥裂—气球模。

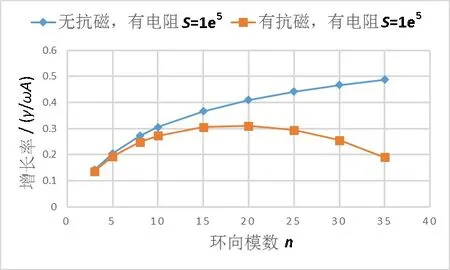
图6 电阻对不稳定性的影响

图7 则是电子粘滞对不稳定性的影响。与图5比较可得，电子粘滞会增加剥裂—气球模的不稳定性，形成粘滞剥裂—气球模。虽然电子粘滞ηH在碰撞等离子体中都是可以被忽略的，但是在碰撞率较低的等离子体中，它的作用是非常明显的。对比图6和图7可以看到，加入电子粘滞之后，不稳定性增长率得到明显的抑制，降低了大约50%。

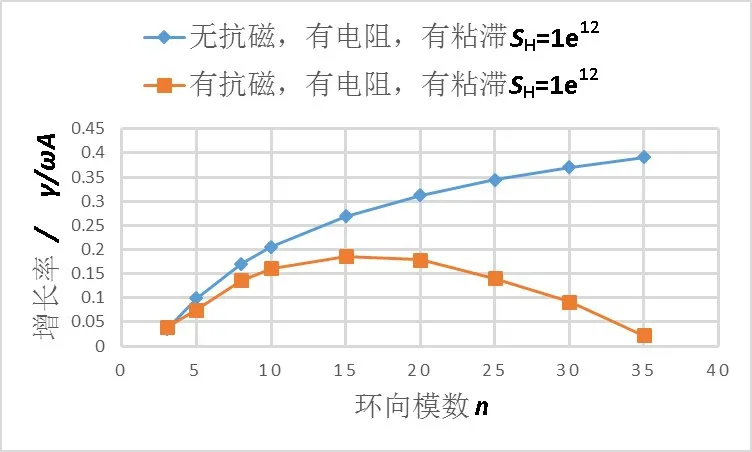
图7 电子粘滞对不稳定性的影响

4 总结

本文分析了托卡马克高约束模式下自发产生的边界局域模的基本特征，基于研究边界局域模的BOUT++三场模型，按照剥裂—气球模型优化，可以解出不稳定性的增长率。模拟结果发现，抗磁效应能显著降低不稳定性的增长率，而电阻效应会增大不稳定性的增长率。压强，电流，磁通等3场线性模拟可以解决产生ELM的剥裂—气球模不稳定性的具体驱动源、不稳定性产生的位置以及空间分布。而为了能够研究湍流和能量输运，ELM是如何崩塌，ELM的能量损失能有多少，就需要在方程中加入新的物理量，在程序中加入新的模块，这将是接下来的研究重点。