基于自适应密度聚类非线性流形学习降维方法研究与实现
陈晋音,郑海斌,保星彤
(浙江工业大学 信息工程学院, 杭州 310023) E-mail:chenjinyin@zjut.edu.cn
1 引 言
流形学习的方法基于数据是采样于一个高维的外围欧式空间的一个低维子流形的假设,流形存在一定的低维内在结构.由于它们在寻求嵌入在高维空间中低维流形表现出突出的结果,并且在实际应用中具有灵活性,因此吸引了大量学者研究.目前具有代表性的流形学习算法有等距映射(Isometric Mapping,ISOMAP)[1]、局部线性嵌入方法(Locally Linear Embedding,LLE)[2]、Laplacian特征映射(Laplacian Eigenmap,LE)[3]等.
但当前普通降维方法降维后对流形产生扭曲,展开后结构发生“畸形”的情况,因此本文希望找到一种方法,这个方法中流形的全局结构可以通过迭代合并相邻局部模型得到,从而得到流形的低维结构.为了克服普通降维方法降维后对流形产生扭曲,展开后结构发生“畸形”的情况,本文提出了一种新颖的流形学习方法,用分段线性模型来近似流形.
2 基于自适应密度聚类的非线性流形学习降维算法
本流形学习降维算法可以分为四个主要步骤,算法流程图如图1所示.

图1 非线性流形学习降维方法的流程图Fig.1 Flow chart of nonlinear manifold dimension reduction algorithm
2.1 形成局部线性模型
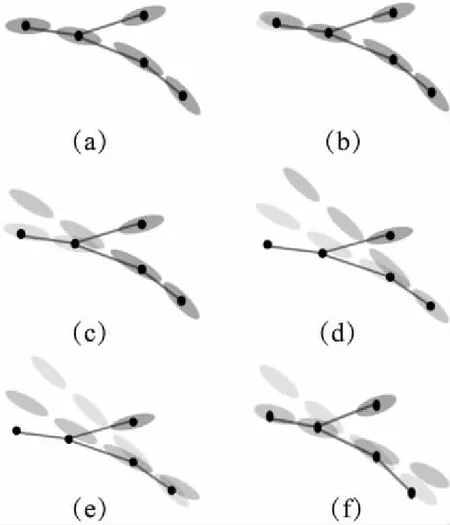
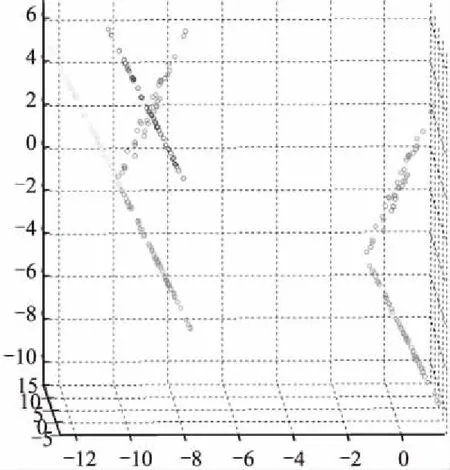
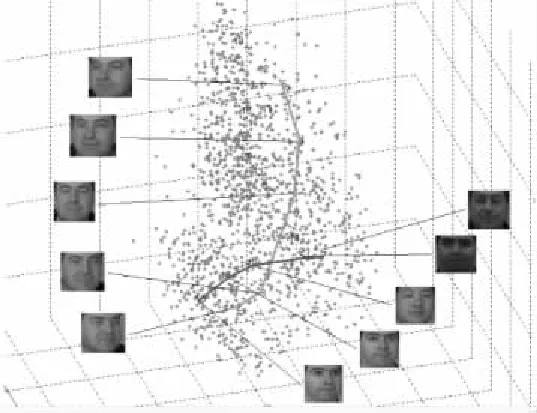
有高维样本M,M的每一个样本为一个点x,这个点通常是一个数学表示的对象.从嵌入了的低维流形(n< 算法的初始步骤是对流形M中的数据对象运用自适应密度聚类算法进行聚类[4],自动确定初始的聚类中心a,并且把M分成c个类,每个类为Cn(n⊂c).一旦X被分割成c个类簇,就可以形成局部线性模型.第k个簇的线性模型为Ck类中所有的数据点XCk投影到超平面,其中超平面的基向量由在数据XCk上运行局部ICA得到的特征向量定义.在每个聚类上运行ICA,将聚类样本映射到n+1维且不改变聚类的关联情况,形成局部低维线性模型. 由于在这个阶段,数据是局部n维的,下一步是对齐局部线性模型建立全局一致的全局模型.这种全局模型仍将被嵌入N维空间,但在局部模型和全局模型是n维的,所以简单的ICA转换将数据的维度降低到n维. 全局遍历的步骤通过将相邻模型的基本向量迭代地遍历合并,并将先前访问的点投影到当前模型的基向量上来执行,如图2所示是按照一定顺序迭代每个模型的过程示意图. 图2 迭代过程示意图Fig.2 Iteration process illustration 对每个线性模型线性模型,采用其聚类中心作为线性模型代表,将所有聚类中心建立一个MST树.MST遍历起点的选择和当存在多个子节点时遍历顺序的选择,对本方法设计结果的影响为零.通过将访问模型合并成全局数据表示,迭代地形成全局模型.最小生成树(MST)提供了局部模型拓扑的表示,因此形成模型访问顺序的基础.模型MST的定义如公式(1)所示. (1) 其中d(ai,aj)是两个聚类中心ai和aj的欧式距离,也是MST树的连边.判断是否能够将聚类中心间连线看作MST树的条件是,要求MST消除所有首尾连接且连边权重最小. 针对已构建的MST,由于在流形上构建的MST不同于普通二叉树每个节点只有两个子树,先序遍历等遍历无法满足本方法的要求,因此设计了一种能够简便遍历含有两个以上子树的MST的方法,该方法实现在遍历过程中能同时对当前和下一个遍历节点进行平行映射.按MST树为基础遍历顺序的具体流程如图3,其中由于返回映射的流程较为复杂,本文单独在图4的流程图中展示. 图3 遍历流形的全局MST流程图Fig.3 Flow chart of MST global manifold process 图4 返回映射的流程图Fig.4 Flow chart of backward mapping 对于前向映射,已访问的模型被投影到当前模型上,使得它们位于相同的坐标空间中.为了减少失真,需要两个模型先平行,这是本流形学习降维算法中关键概念之一的投影的平行化. 前向映射的主要原则是,如果两个模型的法向量对齐,意味着两个模型是平行的,相当于两个模型之间的二面角等于零.因此,目标是找到已访问模型与当前模型对齐所需的旋转角度,使得它们能够旋转后平行.给定两个模型的基向量Vi和Vj,目标是找到将Vi与Vj对齐所需的旋转矩阵Φ,然后应用该旋转矩阵将已访问模型的所有数据点XCi映射到由Vj定义的子空间上.对于每个类的基向量,有子空间的法向量作为基向量组的第(n+1)个向量,因此,矩阵Vi的大小为N×(n+1). 找到旋转矩阵Φ后可以很容易将模型的映射变为点集的映射问题.假设基向量现在为Vi=[v1,v2,...,vn+1],应用公式(2)对每组基向量乘以缩放系数,其中相同向量前的系数的绝对值选取不影响旋转结果,再并上求反的向量组.这样做是为了排除两个轴在相反的方向的情况,并且缩放确保了求得的旋转矩阵唯一. Vi=[v1,2v2,…,(n+1)vn+1,-1.5v1,-2.5v2,…,-(n+1.5)vn+1] (2) Φ=YVT (3) 求出旋转矩阵后对XCi应用公式(4)将两个模型做平行化处理: (4) 其中-Φ为Φ的求反.两个模型平行后将更新Ppre的轴Vi=ViΦ,更新后的V取前n维.然后利用公式(5)将已访问的模型映射到当前模型: (5) 两个模型的旋转及映射步骤分解过程如图5所示. 图5 模型的旋转及映射步骤分解Fig.5 Model rotation and its mapping steps (6) 返回映射和前向映射,都需要对所有之前遍历过的线性模型都施行. 一旦在上述遍历中访问了所有节点,将获得嵌入在N维空间内的流形的n维表示.通过在全局超线性模型上运行ICA再对高维空间的低维线性模型降维,将低维线性模型在低维空间中显示,也就真正实现了对数据高维到低维的降维. 所采用的三个评估条件中的两个涉及到嵌入的局部稳定性,一个用于测量拓扑稳定性(可信度),另一个用于测量几何稳定性(错误率).第三个评估条件是关于数据的全局距离以及此全局结构的维持程度(残差方差误差). 3.1.1 可信度 可信度(TW)衡量邻居在高维空间和低维空间之间的保留.值得信赖的高价值是衡量当地社区在低维空间中的重建程度的一个很好的衡量标准.按照与[6]相同的术语和方法,嵌入在邻域大小区域k的可信度定义为公式(7): (7) 其中Ck是在低维空间中但不在高维空间中的xi的k邻域中的数据样本集合.d(xi,xj)是根据在高维空间中与xi的距离的排序中的数据样本xj的等级.可信度值为1时表示流形学习没有发生局部邻域失真. 3.1.2 映射错误率 映射错误率(PE)测量由于流形学习而引入的局部失真.由于该误差度量是基于Procrustes分析,它测量高维空间中的邻域与低维空间中相同邻域之间的旋转变化.错误度量被定义为公式(8): (8) 其中K(xi,xj)为围绕xi和xj的邻域的Procrustes统计量.PE为0表示在高空间和低维空间中的给定邻域之间的旋转没有变化.函数Rk对缩放敏感,因此会突出那些规范化数据或引入局部尺度变化的技术. 3.1.3 残差方差误差 残差方差误差(RV)测量高维和低维空间中所有点之间距离的差异[7].误差测量为公式(9): R=1-V2(Bx,By) (9) 其中Bx是包含高维空间中所有点之间的距离的正方形对称矩阵(由k个最近邻居形成的测地距离图测量).By是低维空间中的点之间的欧几里德距离矩阵.V2取自Bx和By的所有线性相关系数.RV值为0将表示两个距离矩阵之间的完美相关. 3.1.4 数据集密度分析 处理稀疏数据的能力是多元学习中的开放性问题之一.设置四种不同的数据集大小用于表示数据从稀疏到密集的变化.使用瑞士卷数据集作为测试数据集取样,数据集大小分别设为n=250,500,1000和2000个数据点. 从表1中可以看出,当数据密度低(n<1000)时,特别是当考虑残差时,所有的算法性能都大幅下降,因为稀疏数据中包含的局部和全局信息通常不足以正确地近似流形的形状.当n≥1000时,本算法表现最佳,因为它能够恢复流形的局部和全局属性.通过值的变化,可以看出本算法的性能随着密度的增加而提高.密度低时,本流形学习降维算法的性能将降低,但不会导致算法不可用.因此,只要数据被很好地采样,本降维算法的性能胜过其他流形学习算法. 3.1.5 噪声分析 在实验中使用的噪声模型是平均值为0的高斯噪声,σ=[0,1]范围内的标准偏差.尽管在σ=1的情况下,瑞士卷数据集并不会完全降级,但是许多流形学习算法仍然难以用这种噪声量来获取流形的真实结构. 表1 本算法与典型降维算法针对不同密度数据集的比较Table 1 Comparison between proposed algorithm and baselines 从本流形学习降维算法来看,噪声会影响聚类步骤,因此不仅会导致不正确的模型形成,而且还会产生不正确的MST.如果聚类步骤无法产生准确的数据本地模型,则本流形学习降维算法算法不可能恢复流形的真实嵌入.使用数据集大小为n=2000来排除密度的影响,保证变量仅仅集中在噪声的影响上.图6中表示使用n=2000和σ=1的本算法创建的MST. 图6 用n=2000和σ=1的本流形学习降维算法创建的MSTFig.6 MST generation for proposed manifold dimension reduction algorithm when n=2000 and σ=1 可以看到,跨越流形的MST中出现了短路.这些短路将导致嵌入的失真和重叠,因为合并步骤将合并两个不是拓扑相邻的模型.这就是可信度降低的原因:重叠导致点在非连接邻居之间跳跃. 3.2.1 人工数据 该方法已在瑞士卷(Swiss Roll)人造数据集上测试算法的性能,并将该方法与五个同样数据集上的其他领先算法进行比较.ISOMAP[7]和LLE[8]被用来代表全局和本地的多元化学习方法.由于本流形学习降维算法是局部到全局方法,因此使用三种领先的局部或全局算法分别为局部切空间排列算法(Local Tangent Space Alignment,LTSA)[9],流形学习图表(Manifold Charting)[10]和局部线性协调(Locally Linear Coordination,LLC)[11],降维结果如图7. 图7 (a)至(g)分别为原瑞士卷数据集和ISOMAP、LLE、LTSA、Manifold Charting、LLC及本算法的流形学习降维算法应用于瑞士卷数据集时的结果Fig.7 From (a) to (g),they are switch roll data set,dimension reduction results based on ISOMAP,LLE,LTSA,Manifold Charting,LLC and proposed algorithm respectively 根据降维结果所示,本文可以看出本论文降维算法不仅能完成数据集降维处理的目标,并且相较于其它算法,不会产生数据内在结构的畸形,极大程度保证了本算法结果的正确率和可信度. 3.2.2 COIL-20数据集 COIL-20数据集由围绕一个轴旋转的3维物体的72张图像组成.每个图像的大小为128×128像素,该72个样本形成的流形等同于嵌入在16384维空间内的圆形流形.因此COIL-20数据集在实验中形成的MST的排序没有分支,是一个一维链状模型.同样,可以在MST中的首位两个模型之间建立连接,按照相同顺序在MST的任意一处断开,并不会影响实验结果.由于COIL-20数据集本身是一个封闭的圆柱流形,因此本算法会导致环形流形中某部分断开分裂到低维嵌入的两边,如图8所示是将COIL-20数据集降至二维的低维嵌入,流形的低维嵌入结构并不明显. 图8 将COIL-20数据集降至二维的低维嵌入结构Fig.8 Two dimension mapping structure for COIL-20 data set 进一步将COIL-20数据集视为一维流形,嵌入到一维空间中.使用本算法将COIL-20数据集嵌入一维空间的量化结果如图9所示.通过将数据嵌入到一维空间中,本算法能够较准确的捕获数据的结构,并清楚地按照对象的旋转度显示.因此,在二维嵌入中不明显的结构在一维表示中能被识别. 图9 将COIL-20数据集降至一维的低维嵌入结构坐标图和结果图Fig.9 One dimension mapping location and results based on proposed algorithm for COIL-20 data set 3.2.3 FERET数据集 FERET人脸数据集包括200个人,每个人7张80×80的照片,即一个1400个样本的6400维数据集,每组照片存在不同的肤色、姿态、光照和表情变化.为了找到人脸图片中最重要的几个变化参数,使用本算法降维到三维后结果如图10所示. 图10 将FERET数据集降至三维的低维嵌入图Fig.10 Three dimension mapping based on proposed algorithm for FERET data set 可以看出,根据姿势变化,沿垂直轴移动的路径从上到下表示从向右看到正视到向左看的姿势;根据亮度不同,水平路径表示照明条件发生变化而姿势保持不变. 在本文中,提出了一种基于自适应密度聚类的非线性流形学习降维方法.针对当前普通降维方法降维后对流形产生扭曲导致流形展开后结构发生“畸形”的情况,运用平面的平行映射克服原数据集因为通过降维而产生的畸变.设计算法性能评估指标,针对流形学习参数对降维的影响,设计实验分别并对不同数据集密度和噪声对算法结果影响展开分析,最终验证了提出方法的有效性.并且通过实验测试,证明在人造和实际图像数据集上,本流形学习降维算法与现有最先进的流形学习算法相比,产生良好的降维效果,同时对实验中揭示出的算法在实际应用范围做出相应阐述和分析.2.2 建立最小穿越树MST


2.3 遍历流形的全局MST
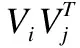

2.4 找到低维嵌入结构
3 性能评价及实验分析
3.1 性能评价及分析


3.2 仿真实验与分析



4 总 结

