BLKF方法抑制MEMS惯性传感器随机噪声

赵 新，赵忠华，曹一文，鲁兴龙

(1.上海交通大学电子信息与电气工程学院，上海 200240; 2.中国华阴兵器实验中心, 华阴 714200)

0 引 言

航姿参考系统(AHRS)是不受外部环境因素干扰，给导航定位提供位姿信息的机载传感器。在AHRS中，受传感器精度等因素的影响， MEMS惯性传感器输出数据与真实数据存在较大误差。为减小误差，提高输出数据精度，在传感器输出数据过程中应用KF算法。为获得误差更小的数据，如文献 [1-8]对卡尔曼滤波算法进行了改进。

在KF过程中，传感器受温度、加速度等因素变化的影响，随机噪声发生变化，根据以往经验取值产生偏差，影响滤波结果。为此文献 [9-16]提出蒙特卡罗随机噪声逼近法、变分贝叶斯测量误差逼近法，它们都能较好地对随机噪声进行修正。同时也存在不足之处，蒙特卡罗随机噪声逼近法在采样过程中需要消耗大量时间；变分贝叶斯法提供了精确的点估计，然而点估计限制了后验分布的范围[17]。针对上述不足，本文提出利用拉普拉斯变换对贝叶斯边缘分布逼近，该方法能够有效避免迭代过程消耗大，同时给出更为准确的近似边缘分布，提高后验精度。

1 模型建立

根据KF原理建立MEMS惯性传感器的滤波方程组，如下所示：

(1)

式中：xn为状态变量，即估计角速度；yn为测量值，即陀螺仪测量角速度；wn为服从正态分布的状态噪声，均值为0，方差为Qn，wn～N(0,Qn)；Vn为服从正态分布的测量噪声，均值为0，方差为Rn,Vn～N(0,Rn);A为动态模型的过渡矩阵；H为测量模型矩阵。

2 理论算法

2.1 贝叶斯滤波

式(1)MEMS惯性传感器卡尔曼滤波方程组用概率形式表示为：

(2)

式(2)的贝叶斯滤波方程形式，由先验分布、似然函数、边缘分布和后验分布四部分组成。其中先验分布表达式为[18-19]：

(3)

似然函数表达式为：

p(yn|xn)=N(Hxn,Rn)

(4)

后验分布表达式为：

p(xn|y1:n)=N(mn,Pn)=

(5)

式中：x0～N(m0,P0)。

2.2 拉普拉斯逼近法

在计算贝叶斯后验分布时，由于边缘分布维数高、数据量大等原因造成其难以计算，本文采用拉普拉斯逼近法对其近似逼近求解，获得有效的边缘分布值[20]。

拉普拉斯逼近方法如下所示：

(6)

(7)

(8)

当λ相当大时，b的积分相当于高斯分布。

(9)

(10)

从上述推导获得拉普拉斯逼近：

(11)

3 BLKF滤波

本文将测量噪声作为随机变量、估计参数，可获得联合先验分布：

p(xn-1,Rn-1|y1:n-1)dxn-1dRn-1

(12)

代入贝叶斯公式中，得到如下方程：

p(xn,Rn|y1:n)=

(13)

上述式(12)和式(13)分别表示贝叶斯卡尔曼滤波预测方程和更新方程。

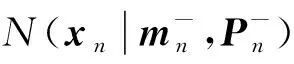
(14)

式中：

(15)

式中：

xn|n-1=Axn-1

(16)

Pn|n-1=APn-1AT+Qn-1

(17)

(18)

(19)

(20)

式中：

通过上述表示，可以获得测量噪声更新步骤。下一步将推导得到的噪声贝叶斯拉普拉斯表示形式代入卡尔曼滤波步骤中。

构建BLKF滤波过程，步骤如下式：

(21)

4 实验室实验

本实验采用的微惯性姿态测量系统是法国SBG公司生产的航姿参考系统。SBG航姿参考系统是法国制造的高精度姿态测量系统，能够为载体提供精准的姿态信息。本文以SBG航姿参考系统输出的角速度信息作为实验数据。

4.1 单角速度旋转转台实验

转台实验中，SBG航姿参考系统单轴以20°/s的角速度随转台旋转，随机噪声项初始值服从正态分布N(0，1)。用KF和BLKF分别对AHRS旋转输出角速度进行滤波，滤波结果如下所示：

惯性传感器在转台旋转时，应用KF和BLKF处理角速度数据后，获得相应的滤波曲线。滤波结果与真实旋转角速度求差，再求均值和方差，结果如表1所示。

4.2 多角速度旋转转台实验

转台在水平面内以-10°/s 、-20°/s、-30°/s、

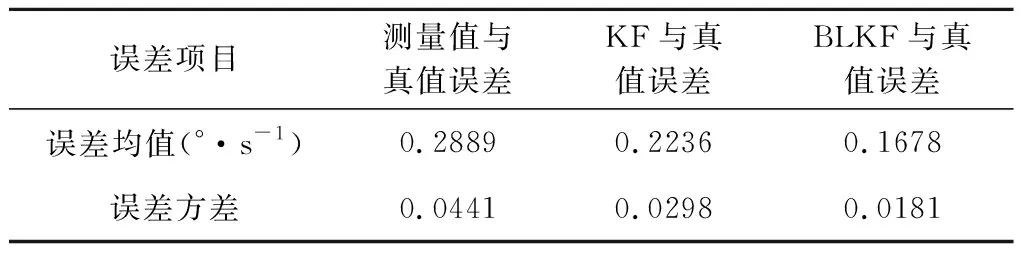
表1 测量值、KF和BLKF与真实角速度误差对比Table 1 Comparison of observed values, KF and BLKF, and true angular velocity errors

-40°/s、-50°/s的角速度旋转，随机噪声项初始值服从正态分布N(0，1)。用KF和BLKF分别对AHRS旋转输出的角速度进行滤波处理，滤波结果如图3、4所示：

惯性传感器在转台旋转时，应用KF和BLKF处理角速度数据后，获得相应的滤波曲线。滤波结果与真实旋转角速度求差，再求均值和方差，结果如表2所示：

4.3 转台实验结果分析

通过对单角速度实验和多角速度实验分析，获得如下结论：当角速度恒定不变时，通过表1中的误差均值和方差可发现，BLKF比KF滤波后的数据更接近真值；当角速度发生改变时(该情况更接近AHRS的真实使用环境，在此过程中无法获知随机噪声的改变)，如图4所示AHRS在长时间使用后, KF无法及时响应，出现使用时间越长滤波误差越大的现象，而BLKF则无该现象出现，说明BLKF能更好的适应角速度改变的情况，获得更为精准的数据；如表2所示，BLKF在变角速度的情况下比KF的误差均值和方差更小，更接近真值。

表2 多角速度测量值、KF和BLKF与真实旋转角 速度误差对比Table 2 Comparison of observed values, KF and BLKF, and true angular velocity errors of any angular velocity

5 结 论

针对MEMS惯性传感器数据处理应用KF时，滤波方程中随机噪声根据以往经验选取，造成滤波结果不准确的问题。本文研究了一种基于BLKF对随机噪声更新的方法，该方法以贝叶斯更新随机噪声为基础，运用拉普拉斯近似算法对边缘分布求解，改进了KF滤波过程，使随机噪声实时更新，增强了滤波后数据的准确性。实验结果表明，该方法能够有效地对随机噪声进行抑制，获得更为准确的滤波信息；同时AHRS动态使用时，BLKF也能对未知随机噪声精准估计滤波，获得准确的滤波信息，为AHRS后续使用提供技术支持。