高斯混合模型优化的四元数约束CKF姿态估计

戴 卿，隋立芬，田 源，曾 添，田翌君

(信息工程大学地理空间信息学院，郑州 450001)

0 引 言

姿态估计技术的基础是姿态表征方法，常见的有欧拉角法、方向余弦矩阵法、姿态四元数法和罗德里格斯参数法。其中欧拉角法表述简单，参数无冗余，但存在奇异现象，且计算量大；方向余弦法可全姿态工作，但参数较多，求解复杂；罗德里格参数描述姿态运动学具有非线性，但会在180°和360°处出现奇异值[1]。四元数法具有全局非奇异和计算量小的优点，逐渐成为GNSS/SINS(Global Navigation Satellite System/Strap Down Inertial Navigation System)姿态更新算法的研究热点。为此文献[2]讨论了基于误差四元数GNSS/陀螺组合姿态确定的数学描述问题及滤波算法，并取得较好成果。而姿态四元数表述的系统常为非线性的，且需顾及归一化约束，否则会引起滤波精度降低，甚至导致协方差矩阵奇异[3]。为解决上述问题，文献[4]提出乘性四元数拓展卡尔曼滤波(Quaternion based Extended Kalman Filter，QEKF)，但该近似线性化的次优滤波存在高阶截断误差影响。文献[5]中四元数无迹卡尔曼滤波(Quaternion based Unscented Kalman Filter，QUKF)，进一步提高了非线性估计的精度，但计算中出现负权值的sigma点，难以确保协方差阵的正定性，且迭代中频繁地与修正罗德里格斯参数进行切换，计算负担偏大。容积卡尔曼滤波(Cubature Kalman Filter, CKF)利用三阶球面—相径容积规则求取非线性函数的后验分布，相比QUKF具有更严谨的理论基础[6]，文献[7]将其与增益修正理论结合，提出了四元数约束的容积卡尔曼滤波(Quaternion based CKF, QCKF)，稳定性和精度更好，较适合高维系统。

以上研究均基于随机模型为高斯白噪声的假设，而实际SINS状态噪声和GNSS量测噪声并非是理想高斯分布，如随机模型失配，就会影响估计精度，严重时导致发散[8]。因此，讨论非高斯噪声下的四元数非线性姿态更新算法，对GNSS/SINS组合测姿应用具有重要意义。为此有学者提出基于乘性误差四元数的抗差自适应滤波，通过构造自适应因子改进估计可靠性[9]。文献[10]用渐消记忆处理量测新息协方差，增加四元数卡尔曼滤波的稳健性。文献[11]提出基于Huber改进的稳健四元数无迹卡尔曼滤波，对量测更新修正，提高算法自适应能力。解决非高斯噪声的另一可行途径是源于高斯混合模型的多模近似方法，将复杂的非线性非高斯系统通过高斯混合滤波进行任意精度近似[12]。比传统处理噪声采用膨大方差的高斯分布近似方法，具有更高的精度。近年来逐渐被认同为一种较好方式，在图像处理、语音识别、信号分析和导航完好性监测等方面研究引起重视[13]。基于此，本文针对GNSS/SINS中噪声随机模型的非高斯分布特性，在多模近似和QCKF算法的基础上，提出基于高斯混合模型的四元数约束容积卡尔曼滤波算法。最后通过仿真测试和实测分析，表明该算法具有更好的自适应性和稳定性。

1 问题描述

xk|k-1=f(xk-1)+gw

(1)

式中：f(·)为非线性系统状态传播函数；g为噪声系数阵；w为系统噪声；详细设置见文献[2]。

GNSS观测数据经卫星钟差、对流层延迟和电离层延迟改正后，整理得量测方程

zk=hk(xk|k-1)+vk

(2)

文献[14-15]通过小波变换和Allan方差对SINS噪声和GNSS噪声残余项进行统计特性分析，发现其不符零均值高斯白噪声特征，是高斯与非高斯的混合分布。因此，为改进滤波算法性能，就必须对其随机模型作进一步精化处理。

2 算法原理

2.1 四元数加权均值算法

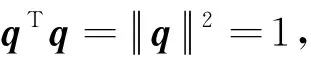
(3)

2.2 高斯混合容积卡尔曼滤波算法设计

引理1. 高斯混合模型可通过分量I的数值，对矢量x的概率密度函数p(x)达任意精度的近似。

(4)

式中：ωi为分量权值；N(x:μi,Pi)为均值μi和方差Pi的高斯分布。将其与QCKF算法结合，得到高斯混合容积卡尔曼滤波。

2.2.1高斯分量建模

非高斯噪声可依据非线性程度和协方差矩阵最大特征值两种方式进行高斯混合模型建模[12]，本文按照后者

(5)

2.2.2时间更新

令状态量、过程噪声及观测噪声建模后的高斯分量数分别为I、J和L，构造容积点ξc,k-1，c代表容积点个数，进行非线性传递

ξc,k|k-1=f(ξc,k-1)

(6)

计算状态预测及其协方差矩阵

(7)

式中：

r=(i-1)·I+j

(8)

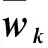
2.2.3量测更新

使用时间更新中产生的容积点，对量测方程进行非线性传递

εc,k|k-1(r)=h(ξc,k|k-1(r))

(9)

计算观测预测及其协方差矩阵

(10)

(11)

状态更新，并计算其协方差矩阵

(12)

(13)

(14)

(15)

式中：n=(r-1)L+l，其中l表示量测噪声中第l个高斯分量。

3.2.4滤波器合并

(16)

(17)

式中：ωk(n)表示第n个高斯分量的权值，其更新方程为

(18)

(19)

2.2.5高斯分量缩减

(20)

(21)

(22)

经由上述计算，可得到状态量的I个高斯分量作为下一时刻滤波递推计算输入。

2.3 两步投影理论

姿态四元数状态量需满足归一化限制，滤波中如不考虑其约束条件，就会降低精度，甚至导致协方差奇异。文献[17]采用四元数强制性约束将姿态估计直接投影到四元数约束表面，未顾及姿态估计方差和四元数等式约束的非线性问题。鉴于此，本处采用两步投影法来解决。在状态变量xk中，误差四元数δq满足c(xk)=δqTδq-1约束条件，则将无约束状态投影到约束表面

(23)

第一步投影，将无约束的状态估计式(21)和(22)投影到约束表面，得到约束的状态分布均值和方差。

(24)

(25)

2.4 算法实现流程

(1)利用式(4)和(5)对SINS过程噪声和GNSS观测噪声进行非高斯建模。

(2)状态预测。根据系统方程式(1)和式(6)～(8)估计滤波器在k时刻的状态预测值，其中四元数加权均值由式(3)求解。

(3) 观测更新。通过观测方程式(2)，利用式(9)～(15)进行量测更新，并完成高斯分量的合并与缩减后，最后根据式(24)～(25)对四元数状态量进行规范化约束，得出当前时刻的姿态估计信息。

3 仿真校验

为验证算法的有效性，采用GNSS/SINS紧耦合仿真平台。部分仿真参数设置如下：陀螺仪刻度系数0.2%，随机游走2°/h， 零偏0.1°/h；加速度计刻度系数0.3%，随机游走30 μg/h，零偏0.1 mg；初始姿态误差协方差20″，初始速度协方差10 cm/s, 初始位置由伪距单点定位确定，误差协方差3 m。 基于2017-1-23的卫星星座分布和当前历元姿态仿真GNSS观测数据，GNSS接收机钟差和钟漂协方差分别为10 m和10 m/s，由0.9 N(0,0.52)+(1-0.9) N(0,0.82)模型产生非高斯噪声。采用三种不同滤波方案，对高斯白噪声和非高斯噪声污染两种情形处理，选取1000个历元解算结果分析。(计算平台：华硕Inter Core i5-4460, CPU 3.2 GHz, RAM 6 GB，Matlab R2014a)

方案1：乘性四元数的扩展卡尔曼滤波

方案2：四元数约束容积卡尔曼滤波

方案3：高斯混合四元数约束容积卡尔曼滤波

图1和图2对比两种情形下不同滤波方案的姿态估计效果。由计算结果可以看出：

(1)在高斯白噪声假设条件下(图1)，以上方案均达到较好的姿态估计结果。其中方案1略低，因为QEKF在含有初始姿态角误差的情况下，其高阶截断误差对滤波精度和稳定性产生了影响。而后两种方案是基于CKF框架的，其多元函数代表的思想能够以更高的精度逼近后验均值和方差，使计算精度进一步提高。

(2) 当GNSS/SINS中噪声受非高斯噪声污染时(图2)，方案1和方案2稳健性较差，姿态估计误差明显增大。而方案3是一种基于高斯混合模型的自适应滤波算法，对随机模型精化处理，未出现明显的发散现象，算法收敛精度较高，性能较为稳定，明显优于前两种算法。

为体现算法比较的公正性，在仿真条件不变的情况下，进行了50次蒙特卡罗实验，用俯仰角、横滚角和航向角的均方根误差(RMSE)来衡量精度，用平均耗时衡量计算效率，结果如表1所示。方案3估计精度优势明显，但计算负担偏大。因为容积变换产生的每个sigma点本质上都将进行一次导航解算，状态维数越大，产生的sigma点越多，导航解算的次数也就越多，算法占用的时间也就比方案1基于模型线性化的多。且采用多模近似方法精化处理随机模型，由高斯混合模型分若干子滤波器对状态参数进行更新，计算量则进一步增加。

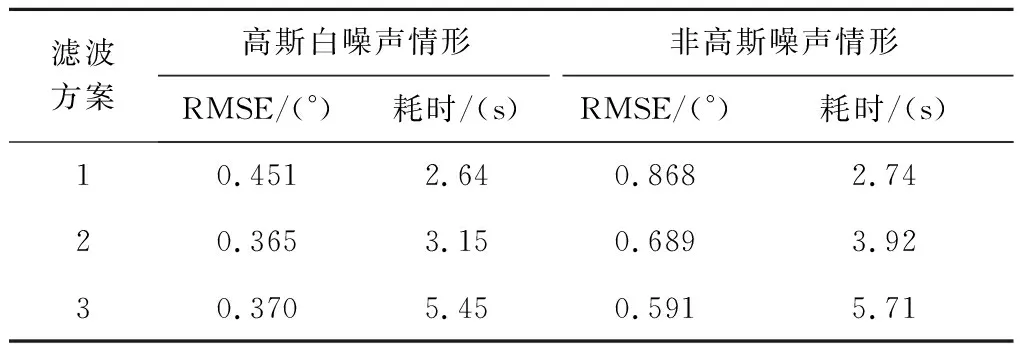
表1 三种方案性能比较Table 1 Comparison of different filter performance

4 试验数据测试

试验场地位于郑州市，GNSS接收机可接收GPS和BDS双系统信号，采样率1 Hz；惯导精度较高，标称陀螺零漂小于0.02 °/h，采样率200 Hz，设备均安装于汽车上，将高精度的GNSS RTK/SINS数据作为参考真值进行比较。轨迹沿途有建筑物、树林和水面，数据采集环境较为复杂，可导致明显的多路径误差，使得GNSS观测噪声失去高斯白噪声特性。选取1000个历元数据，采用仿真校验中的方案2和方案3进行滤波处理。表2分析了卫星高度角较高的SV2和较低的SV8噪声特性，发现SV8观测噪声峭度远小于3，呈现负峭度，表现出较明显的非高斯特性。图3分析了陀螺Allan方差，发现惯性元件是含有角度随机游走、量化噪声、零偏不稳定性和速率斜坡等的复杂噪声项。

表2 GNSS伪距噪声分析结果Table 2 GNSS observation noise analysis results

图4至图6中方案3的姿态估计变化范围的最大值小于方案2，由此可知，当载体处于机动状态或多路径效应下受非高斯噪声影响时，本文提出的滤波算法能显著提高姿态估计精度。对于定量的精度比较见表3，方案3的估计精度优势明显，尤其在航偏角上比方案2的估计精度提高了约27%。

表3 两种滤波算法的姿态估计性能比较(RMSE)Table 3 Attitude estimation performance comparison (RMSE)

为进一步验证算法的性能，选取不同长度的数据分析。表4所示随数据量增加，滤波解算精度逐渐降低，但方案3精度始终优于方案2。在试验数据为1000组时，姿态估计精度上方案3较方案2提高约31%，在3600组时，新算法精度改善更为明显，约为39%。因为位置解算跟姿态精度相关，姿态角精度对定位的影响也是明显，因此方案3的位置估计性能也优于方案2。由此可见，本算法在多路径环境下表现出较高的精度，且在长时间的导航计算中，也具有更好的稳定性。

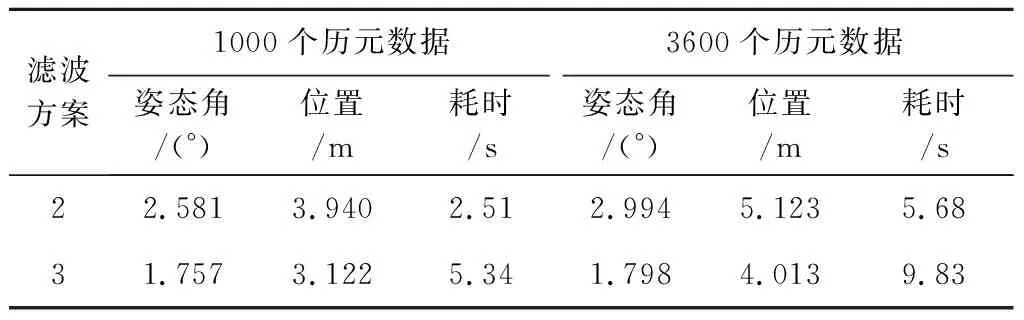
表4 精度和耗时分析Table 4 Analysis of RMSE and calculation time

5 结 论

针对GNSS/SINS紧耦合中四元数更新算法在高斯白噪声假设情况下产生的估计精度下降问题，将四元数约束算法与容积卡尔曼滤波结合，并在高斯混合滤波框架下，提出了一种基于高斯混合模型的四元数约束容积卡尔曼滤波算法。本算法以四元数CKF为基础，解决了四元数姿态的确定问题，并通过高斯分量对GNSS/SINS噪声多模近似，将过程噪声和观测噪声建模为多个分量的形式，精化了滤波的随机模型。最后通过数据测试，验证了GM-QCKF的有效性，表明了将该算法用于非高斯噪声影响下的导航解算中，具有更好的姿态估计精度和自适应性，对于长航时滤波解算具有更好的稳定性。