考虑地层伤害影响的钻井液侵入模拟研究

范宜仁,王小龙,巫振观,吴俊晨,贾建涛

(1.中国石油大学(华东)地球科学与技术学院,山东 青岛 266580;2.海洋国家实验室海洋矿产资源评价与探测技术功能实验室,山东 青岛 266071;3.中国石油大学CNPC测井重点实验室,山东 青岛 266580;4.中国石油技术开发有限公司,北京 100025)

0 引 言

在过平衡钻井中,钻井液固相及其滤液在正向压差作用下侵入渗透性地层,导致电测井模型构建及储层评价困难。为明确钻井液侵入机理及测井响应钻井液侵入校正方法,国内外学者开展了大量的研究工作。钻井液侵入物理模拟方面,Jiao等[1-2]利用柱塞岩心进行钻井液动、静滤失实验来研究钻井液滤失规律;陈福煊等[3]建立了砂槽物理实验来研究钻井液侵入对地层电阻率的影响;Ferguson等[4-5]采用模拟井研究钻井液侵入现象。钻井液侵入数值模拟方面,张建华等[6]对钻井液侵入过程进行了一维数值模拟。当考虑重力作用时,常文会等[7]对钻井液侵入过程进行了二维数值模拟。为研究斜井钻井液侵入储层的井周岩石物理特征,邓少贵等[8-9]开展了斜井钻井液侵入数值模拟,Salazar等[10]比较了油基和水基钻井液侵入对储层的影响,Wu等[11]对水基钻井液性质和岩石物理参数对泥饼生长和侵入速率的影响进行了数值模拟。

受限于实验条件,前期工作多集中于储层性质及泥饼影响,而没能考虑钻井液固相颗粒及其滤液的侵入导致的储层性质变化及对钻井液侵入规律的影响。本文在泥饼动态生长模型的基础上,结合地层模块尺度钻井液侵入物理模拟系统[12-13]观测数据,建立了近井眼储层孔隙度渗透率模型,研究考虑地层伤害影响的钻井液侵入规律,以期为提高电测井模型构建及储层评价提供依据。

1 钻井液侵入有限差分数值模拟

1.1 差分格式推导

当地层中仅含油相和水相,忽略重力与毛细管压力,钻井液侵入过程中符合等温达西渗流,则近井壁区域中的孔隙压力和含水饱和度可由油水两相渗流方程求解[14]

(1)

(2)

pw=po

(3)

So+Sw=1

(4)

式中,ρw和ρo分别为水和油的密度,kg/m3;K为地层绝对渗透率,μm2;Kro和Krw分别为油和水的相对渗透率;μo和μw分别为油和水的黏度,Pa·s;pw和po分别为水相和油相的压力,Pa;φ为储层孔隙度;Sw和So分别为地层含水饱和度和含油饱和度;t为侵入时间,s。

式中,rw为井径,m;re为计算模型半径,m;pe为地层原始压力,Pa;pw为井内钻井液压力,Pa;Swin为初始含水饱和度;Sor为残余油饱和度。

柱坐标系下,式(1)和式(2)化为

(11)

(12)

对于油相方程,对式(11)进行差分离散,得

(13)

同理,对于水相方程,对式(12)进行差分离散,得

(14)

由式(4),将式(13)和式(14)进行合并,可得

(15)

式中,

(16)

(17)

式中,cf、co、cw分别为孔隙、油和水压缩系数,Pa-1。

(18)

式(18)可表示为

(19)

当j=2时,结合边界条件式(7),有

(20)

当j=M-1时,结合边界条件式(8),有

(21)

将式(19)、(20)、(21)写成矩阵形式为

(22)

钻井液侵入过程中,当地层水矿化度与侵入的钻井液滤液水矿化度存在差异时会发生盐分混溶,采用离子对流扩散方程求解水的矿化度[15]

(23)

式中,Cw为水的矿化度,mg/L;kD为弥散系数,m2·s-1。公式左边第1项因式反映了流体流动产生的矿化度变化,即对流部分;第2部分因式反映了盐分浓度差引起的矿化度变化,即扩散部分。

初始条件和边界条件为

式中,Cwin为原始地层水矿化度,mg/L;Cmf为钻井液滤液矿化度,mg/L。

柱坐标系下,式(23)化为

(27)

对式(27)进行差分离散,得

j=3,…,M-2

(28)

当j=2时,结合边界条件式(25),有

(29)

当j=M-1时,结合边界条件式(26),有

(30)

将式(28)、(29)、(30)写成矩阵形式

(31)

钻井液滤液侵入到渗透性地层的同时,钻井液中的固相颗粒逐渐沉积在井壁上形成一层渗透性很差的泥饼,泥饼参数是影响钻井液侵入的主要因素之一。泥饼渗透率、泥饼孔隙度随时间的变化可表示为[11]

(32)

(33)

式中,Kmc和φmc分别为泥饼渗透率和孔隙度;pmc为泥饼内外压差;Kmco和φmco分别为泥饼参考渗透率和参考孔隙度;ν和δ分别为泥饼压缩指数和相渗关系因子。计算时,渗透率取mD*非法定计量单位,1 mD=9.87×10-4 μm2,下同为单位,压力取psi*非法定计量单位,1 psi=6 894.76 Pa,下同为单位,其他参数无量纲。

为了将泥饼动态生长模型和油水两相渗流模型进行耦合,将泥饼作为第1个网格变量,整个模拟区域在径向上采取非均匀网格,内外边界均采取定压边界条件,实现钻井液侵入模拟。

式(22)和式(31)都为三对角方程的线性方程组,为提高求解效率和减少对内存的占用,采用“追赶法”进行求解,即可得到不同侵入时间的压力、含水饱和度和地层水矿化度的径向分布,进而通过阿尔奇公式可确定相应的地层电阻率径向分布[16]

(34)

式中,Rt(r,t)、Rw(r,t)、Sw(r,t)分别是某一时刻地层电阻率径向分布、地层水电阻率径向分布、含水饱和度径向分布;m是孔隙度指数;n是饱和度指数;a为岩性指数。

其中,地层水电阻率Rw(r,t)采用式(35)计算

(35)

式中,Cw(r,t)为某一时刻地层水矿化度径向分布;T为地层温度,℃。

1.2 模型验证

为验证模型正确性,与已发表文献[10]的模型在相同参数设置下进行计算对比(见图1)。基本的储层和流体参数见表1。

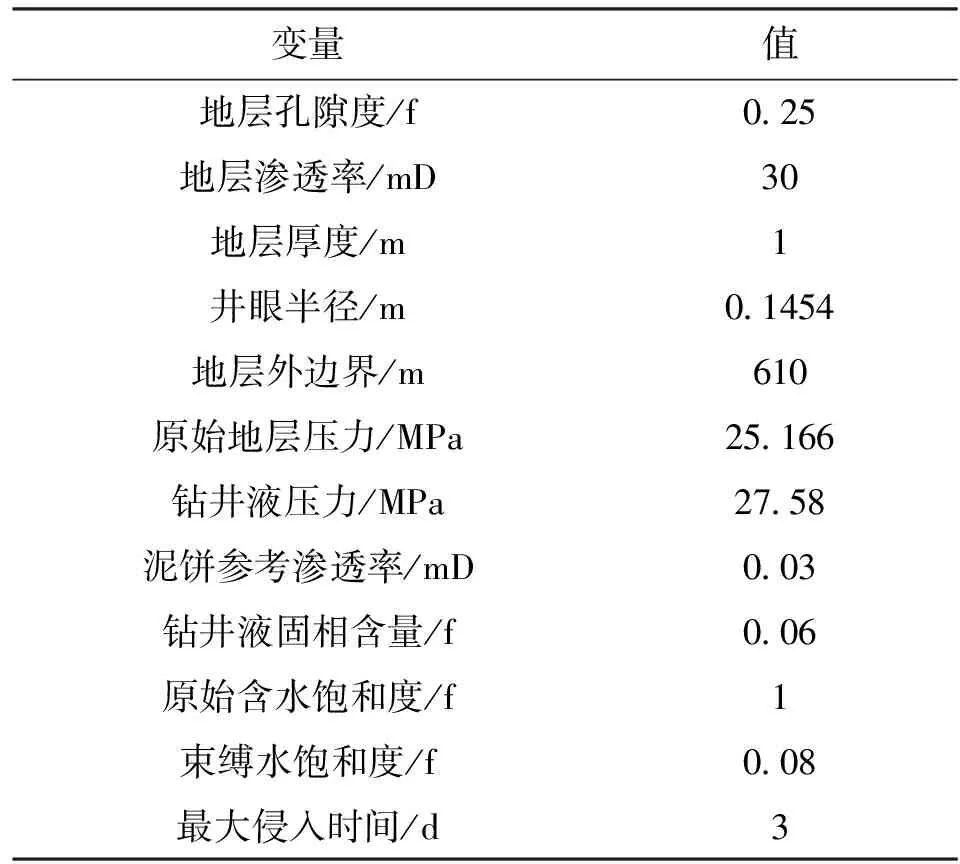
表1 部分地层和流体参数

对比发现,用本文程序得到的不同时间的含水饱和度径向分布和已发表文献[10]中对应的曲线基本吻合,从而证实了本文自主开发的数值模拟程序的准确性。

2 钻井液侵入储层孔隙度渗透率模型

2.1 模型建立

图1 侵入剖面含水饱和度分布

钻井液滤失过程中,虽然钻井液固相颗粒在井壁上逐渐沉积并形成一层渗透性很差的泥饼,但钻井液中更小的颗粒和滤液还会侵入地层造成内部地层伤害,使近井眼储层孔隙度和渗透率降低[17]。

考虑到不同径向深度处地层伤害程度不同,越靠近井眼边界,地层伤害越严重,而越靠近原状地层,地层伤害越轻微,采用线性插值近似计算从井壁地层到钻井液侵入前沿地层不同径向深度处的储层孔隙度和渗透率,如式(36)和式(37)。

(36)

(37)

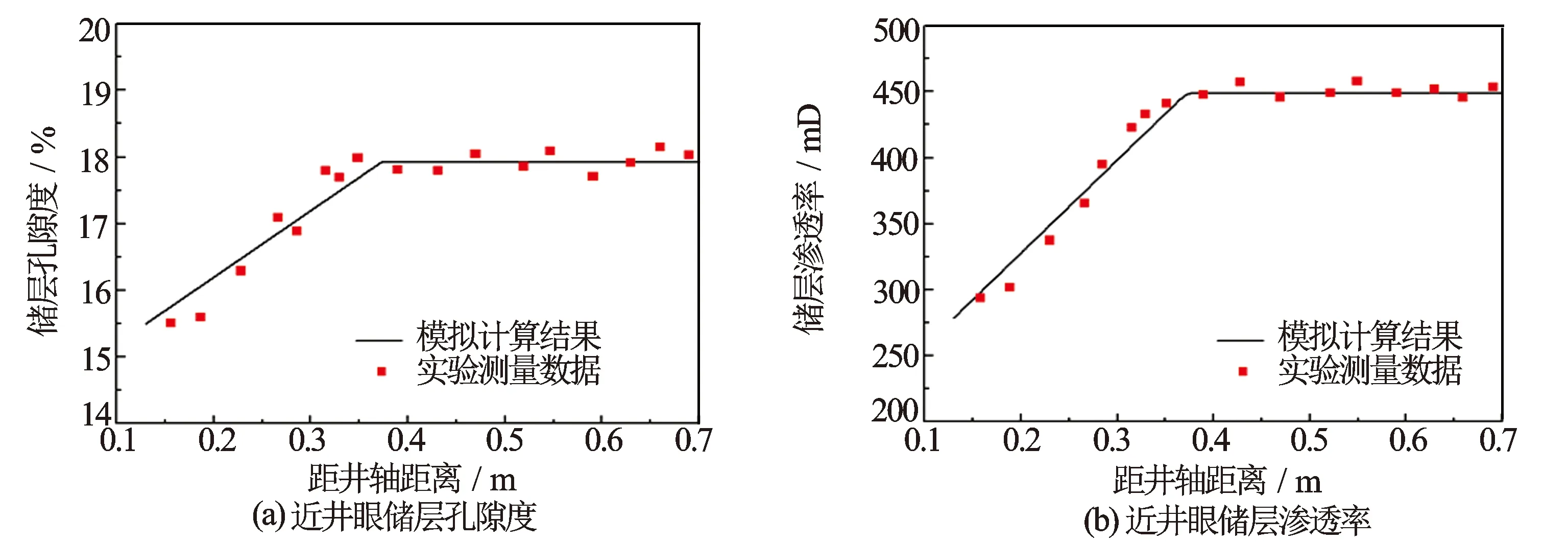
图2 近井眼储层孔隙度渗透率模型验证

式中,rw为井眼半径,m;r为径向侵入深度,m;ri为侵入半径,m;φ0为地层伤害后靠近井壁处地层孔隙度,%;φf为原状地层孔隙度,%;K0为地层伤害后靠近井壁处地层渗透率,μm2;Kf为原状地层渗透率,μm2。

钻井液滤液侵入地层造成地层电阻率在径向上的变化,这种变化是渐变的、连续的。根据地层电阻率径向变化的特点,求解出地层压力、含水饱和度、矿化度的径向分布,再通过阿尔奇公式求得地层电阻率的径向分布,以此确定侵入半径ri,其标准为

|Rt-Rri|/ri<β

(38)

式中,Rt为原状地层电阻率;Rri为径向半径ri处电阻率;β为百分数,可取5%,10%,…,50%等值。根据研究区的地层特征选取β值,即可算出满足这个标准的侵入深度ri,本文模拟中选取β为10%。

2.2 模型验证

将本文提出的近井眼储层孔隙度渗透率衰减模型的计算结果与实验测量结果进行对比,以验证钻井液侵入储层孔隙度渗透率模型的准确性。实验以新型钻井液侵入多功能物理模拟系统[12]为平台,以大尺寸扇形块状结构的砂岩地层模块为实验对象。与传统柱塞岩心尺度下的实验相比,实验保证了钻井液滤液侵入的渗流形态与井下实际情况相同,井眼水动力环境、泥饼形成条件与实际钻井过程更接近,实验规律更为真实可靠。砂岩地层模块的原始孔隙度为17.92%,原始渗透率为449.44 mD。地层水矿化度为30 g/L,钻井液压差4.0 MPa,滤失类型为动滤失,实验温度为25 ℃。实验中所采用的钻井液配方:膨润土42.0 kg/m3,高黏乙烯1.6 kg/m3,聚丙烯酰胺2.1 kg/m3,聚丙烯酸钾1.1 kg/m3,金属熬合聚合物1.1 kg/m3,成膜树脂防塌剂1.1 kg/m3。实验结束后,钻取侵入179 h后不同径向深度处的岩样,测量其孔隙度和渗透率。图2为模型计算结果与实验测量数据对比图,钻井液侵入后离井壁最近处的地层孔隙度减小为15.5%,渗透率降低为278.65 mD。可以看出,模型计算结果与实测规律基本吻合:靠近井壁处地层伤害较严重,储层孔隙度和渗透率衰减较多,而远离井壁地层伤害越来越轻;在未受钻井液侵入段,地层没有受到伤害,储层孔隙度渗透率与原状地层一样。

3 钻井液侵入特征分析

基于建立的近井眼储层孔隙度渗透率模型进行不同物性储层、不同侵入时间下数值模拟,并与相同条件下无地层伤害时的数值模拟结果进行对比,不同物性储层、不同侵入时间的含水饱和度和电阻率径向剖面如图3至图5所示,其中实线表示无地层伤害时的数值模拟结果,虚线表示考虑地层伤害时的数值模拟结果。数值模拟时的地层含油饱和度为50%,地层温度为100 ℃,地层水矿化度为30 000 mg/L,钻井液滤液矿化度为2 000 mg/L,钻井液侵入时间为0.5、1、2、4、8 d和16 d。

图3为储层孔隙度为0.03,渗透率为0.1 mD时不同侵入时刻含水饱和度和电阻率剖面。考虑地层伤害时的侵入深度比不考虑地层伤害时的侵入深度更浅,且侵入时间越长,两者差异越大。图4为储层孔隙度为0.05,渗透率为1 mD时不同侵入时刻含水饱和度和电阻率剖面。考虑地层伤害时的侵入深度与不考虑地层伤害时的侵入深度的差异很小,可以忽略不计。图5为储层孔隙度为0.1,渗透率为10 mD时不同侵入时刻含水饱和度和电阻率剖面。考虑地层伤害时的侵入深度与不考虑地层伤害时的侵入深度完全一致。

为进一步研究地层渗透率对侵入深度的影响,计算了不同渗透率条件下考虑地层伤害影响的侵入深度和不考虑地层伤害影响的侵入深度(见图6)。当地层渗透率大于1 mD时,考虑地层伤害影响的侵入深度与不考虑地层伤害影响的侵入深度一致,而当地层渗透率小于1 mD时,考虑地层伤害影响的侵入深度比不考虑地层伤害影响的侵入深度浅,且地层渗透率越低,两者差异越大。分析认为这主要是因为泥饼在不同物性储层中的形成快慢存在较大差异决定的,当地层渗透率大于1 mD时,泥饼在几分钟甚至几秒钟内就可形成,钻井液侵入将完全由泥饼性质决定,而不是地层;而当地层渗透率小于1 mD时,泥饼形成需要数小时,比在高渗透率地层中的形成速度慢得多。

图3 储层孔隙度为0.03,渗透率为0.1 mD时不同侵入时刻含水饱和度和电阻率剖面

图5 储层孔隙度为0.1,渗透率为10 mD时不同侵入时刻含水饱和度和电阻率剖面

图6 不同渗透率条件下钻井液侵入16 d时的侵入深度

4 结 论

(1) 基于油水两相渗流方程,结合泥饼形成机理,建立了含泥饼动态生长的钻井液侵入数值模型,并与已发表文献的模型进行了计算对比,验证了本文模型的正确性。

(2) 充分考虑钻井液固相颗粒及其滤液侵入对井周地层造成的伤害,建立了近井眼储层孔渗衰减模型,模型结果与地层模块钻井液侵入实验数据具有较好的吻合性。

(3) 当地层渗透率大于1 mD时,考虑地层伤害影响的侵入深度与不考虑地层伤害影响的侵入深度一致;而当地层渗透率小于1 mD时,考虑地层伤害影响的侵入深度比不考虑地层伤害影响的侵入深度更浅,且侵入时间越长,两者侵入深度的差异越大。