如何在大学工科数学教学中强化基础知识的教学
付 瑶 宋东哲 赵玉娟
(吉林大学数学学院公共数学教学与研究中心,吉林 长春 130012)
众所周知,在大学工科众多课程中,数学是一门非常重要的基础课。一般包含:高等数学、线性代数、概率论与数理统计。一方面,数学理论、方法是学生学习后继课程的基础;另一方面,在数学近两学年的教学中,在传授知识的同时,逐步培养学生抽象思维、逻辑推理、创新创造能力也是大学培养人才的一个重要的教学环节。
而数学的特点是概念抽象、推理严谨、内容衔接紧密、逻辑性强。这也给学生学习带来很大困难:前面概念理解不透,后面定理就很难深刻透彻地把握;而基本定理掌握不好,定理的推广应用也就无从谈起。
那么,如何强化基础知识教学,使学生深刻理解掌握基本概念、基本定理,进而在解题中能融会贯通举一反三呢?本文从以下几个方面做了一些尝试和探讨。
一、从四种命题的不同角度,反复讨论同一知识点
大家知道,原命题、逆命题、否命题、逆否命题知识是中学数学逻辑的内容。而许多同学,对四种命题关系还不够清晰,或是不能应用到大学数学具体问题中去。我们要学生掌握好基本概念,并不是要求其如何背得滚瓜烂熟,而是能深刻透彻理解、并会应用。如数列{xn}收敛和有界的关系。原命题是:“如果{xn}收敛,则{xn}一定有界”,则其逆否命题:“如果{xn}无界,则{xn}发散”一定成立,教师可引导学生根据数列无界去判别它一定发散。例如一定发散。同时强调,该命题的逆命题、否命题并不成立,即“有界未必收敛”、“发散未必无界”,例如{(-1)n+1}是有界的,因│(-1)n+1│≤1,而它是发散的。
又如,在高等数学中,数列极限的四则运算法则是一个重要的知识点。如“和”的运算法则是:“如果数列{xn}收敛于A,数列{yn}收敛于B,则数列{xn+yn}一定收敛于A+B ”,这个定理告诉我们的是:“如果两个数列都收敛,则相加以后的新数列仍收敛”。在教学中,教师可引导学生通过例子分析其逆命题并不成立,即{xn}、{yn}均收敛是{xn+yn}收敛的充分条件,而不是充分必要条件。如数列{(-1)n+1}、{(-1)n}都是发散的,但{(-1)n+1+(-1)n},各项全为0,是收敛的,进而启发学生去思考两个数列,如果都收敛,则其和一定收敛;如果都发散,其和也可能收敛;如果一个收敛、一个发散和的敛散性怎么样?更深一层,要求学生能将此结论引申推广,比如尝试讨论更复杂的两数列乘积的极限情况,另一方面能举一反三,能把这部分结论方法应用到其它,如连续性、可导性、可积性等诸多类似问题中去。
二、将抽象问题形象化、具体化
如在线性代数课程中,矩阵的秩是一个非常抽象的概念,而定理“矩阵和的秩小于等于矩阵秩的和”,即“R(A+B)≤R(A)+R(B)”的理解和证明也是学生学习的一个难点。一般教材都是在讲完向量组的秩后利用矩阵的秩就是其行(或列)向量组的秩,再将A+B的行(或列)用A、B的行(或列)线性表示出来,然后利用向量组秩的结论才能给出这个定理的证明。所涉及的几个定理都很抽象,不易理解;而如果利用矩阵行列式秩的概念,即矩阵的秩是其非零子式的最高阶数,再构造矩阵则显然 R(C)=R(A)+R(B),再对 C 进行初等变换,将C的后m行依次加到前m行,后n列依次加到前n列上,即因A+B为D的一个子块,同样利用较形象的行列式秩定义,则显然R(A+B)≤R(D)=R(C),这个结论就容易理解和把握了。
三、引导学生掌握各概念、定理的实质,借助图表等来揭示其中的本质联系
在多元函数微分学中,函数可微、连续、可偏导等概念之间的关系涉及的知识点很多,学生容易混淆,而借助如下关系图:

从上至下是函数可微、连续、有极限的关系,一元函数、多元性函数性质相同;从左至右是二元函数和一元函数的相应的关系。所涉及的十多个结论就一目了然了。
四、在处理较难的知识点时,注意启发学生抓问题的关键点
如学生易将一元函数“可导一定连续”用到多元函数,得到“偏导存在一定连续”。如上图,这是不成立的,关键在于“偏导”是x或y的一元函数(平行x轴或y轴特殊方向)的导数,而“连续”是多元函数“全面连续”,即当动点 P(x,y)依任何方式趋于定点P0(x0,y0)时,二元函数f(x,y)的极限都存在并且为f(x0,y0),问题的关键在于“特殊”和“一般”,“偏”和“全”,不能以偏概全!
五、借助典型例题,帮助学生理解和记忆
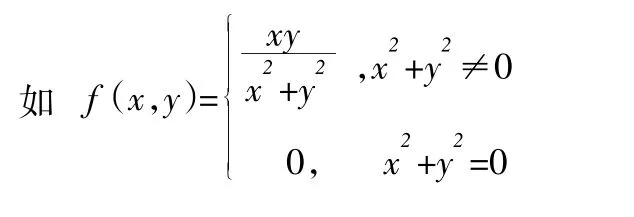
在多元函数微分学中就是一个很典型的问题,它在O(0,0)处二重根不存在,从而不连续;但一元函数f(x,0)、f(0,y)连续,且fx(0,0)、fy(0,0)都存在,可以用来帮助同学来理解和记忆一元函数和多元函数的关系,偏导存在函数不一定连续等重要结论。又如二元函数z=xy的图形是双曲面抛物面(鞍形曲面),原点O(0,0)是它的驻点,但非极值点,借助其图形帮助学生理解驻点未必为极值点,结论就直观、形象容易把握了。
六、将综合问题分解、通过阶梯训练强化基本知识点的教学
所谓难题,一类是技巧性强,解题思路不好把握;另一类就是综合性强,一个题涉及好几个知识点,而每个知识点都是我们强调的基本问题。对这种问题,我们要引导、启发学生深入细致审题,将所涉及的知识点逐层分解,找到各知识点解决的关键点、整个题目也就迎刃而解了。如下体是非数学专业大学生数学竞赛的试题,求极限:
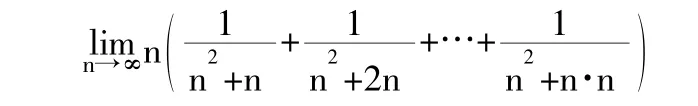
给出题目,要注意引导、启发学生该类求n项和极限问题解题思路。
首先看看能否恒等变形,如能,先变形;不容易恒等变形的,试试两边夹准则,将其放大、缩小,看两端的极限是否相同,本体放缩以后极限不同,所以也不能直接有两边夹准则得出极限;然后考虑能否用定积分定义处理特殊数列的极限……。而本题就是综合两边夹准则和定积分定义得出。
本文虽是从六个方面探讨了如何在工科数学教学中强化基本概念、基本定理等基础知识的教学,将其应用在各门课程,并取得了较好的教学效果。但数学课程本身的特点和工科整体教学要求也决定了在这些方面分作为老师还有很多工作要做,要进一步研究探索。工科数学,其抽象性、严密性也决定了它是诸多课程中最锻炼人思维的一问学科,而如何在教学中深入浅出、循序渐进地传授基础知识,同时注重学生数学思维方式方法的掌握,逐步锻炼培养学生分析解决问题的能力也是摆在广大数学教师面前一项永远也做不完的课题!

