推导“可倒摆实验”原理的新方法

张诺亚

（郑州外国语新枫杨学校，河南 郑州 450000）

重力加速度是物理中一个非常重要的物理量，通常g是指地球地面的物质受到引力的作用在真空中下落的加速度。随着重力发现，学者也开始对它进行更深入的研究，第一个问题就是怎么对它进行测量。

随后，伽利略发现了摆的等时性，惠更斯发现摆的摆动周期和当地的重力加速度成反比和摆长的平方根成正比。于是，人们就利用测定摆的摆动周期的方法，来测量重力加速度。1818年，由凯特（Kater)提出一种新的测量方法，设计出了一种物理摆，即凯特摆（也称“可倒摆”，本文称为“可倒摆”）。波斯坦大地测量研究所曾花了8年测得当地重力加速度是g=(981.274±0.003）cm/s，因达到6位有效数字，故各地对g的相对测定，均以此为依据，很多地区的g值都曾以此为根据，进行相对测量而得到。

以往，一些对于“可倒摆实验”的研究多集中在对实验装置的改进和实验过程的优化，使整个实验更易于操作。在实验原理上，学生需要先理解复摆相关知识才能进行推导。本文从实验中的“可倒摆实验”的整个运动过程出发，应用能量的观点进行分析研究最终得出正确结果。本文的推导过程在关注整个运动过程的同时，也应用更加基础的知识点，使更多不同知识储备的实验者都能很好地理解，结合对实验过程的优化，将更利于“可倒摆实验”的推广。本文将先介绍传统对“可倒摆实验”原理的推导过程，然后使用能量观点对实验原理进行推导解释。

1 从复摆到 “可倒摆实验”原理的推导

首先介绍单摆概念。如果把尺寸很小的物体悬于一端固定的长度为 l且不能伸长的细绳上，使细绳和过悬点铅垂线成角度小于10°（此时应用到数学上的小角近似的概念），放手后可以观察到摆锤周期振动，其周期摆的长度以及重力加速度g有关，其运动状态可用简谐振动公式表示，这样的摆称为单摆。单摆的周期公式为：

其中：T为摆动周期；l为摆长；g为重力加速度。可见，摆的运动周期与摆的长和所在地的重力加速度相关。

然后介绍复摆相关概念，已知质量为m的一个刚体，重心G到转动轴O的距离为h，绕O轴的转动惯量为I。在这里，我们引入小角近似，当摆幅足够小时，刚体绕O轴的摆动周期T可以被近似表示为：

复摆绕通过重心G的转动轴的转动惯量为IG，当G轴与O轴平行时，有：

代入式（1）得：

对比单摆的周期公式(1)，可得：

其中，l称为复摆的等效摆长。因此测出周期T和等效摆长l可求得重力加速度g。

图1 “可倒摆实验”摆杆示意图

图1 是“可倒摆实验”摆杆的示意图，对“可倒摆实验”而言，两刀口间的距离就是摆的等效摆长l。确定两刀口位置后，调节摆锤位置可使正、倒悬挂时的摆动周期T1和T2保持近似相等，即T1≈T2。由公式（3）可得：

其中，T1和h1为摆绕转动轴O轴的摆动周期和旋转中心到重心G的距离。当T1≈T2时，h1+h2=l即为等效摆长。由式（5）和（6）消去IG，得：

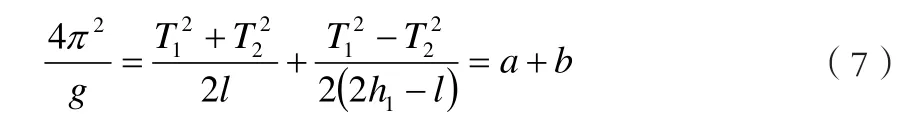
式中，a项可以精确求得，b项无法精确求得。当T1＝T2以及|2h1-l|的值较大时，b项的不精确对测量结果产生的影响忽略不计。具体数据分析不是本文论述重点，请参见相关实验介绍和文献。

2 用能量观点对实验原理进行的推导

以下应用能量观点推导实验原理。

实验中，摆锤运动过程为周期运动。在这里，所关注的分析整个运动周期的能量转化，是接下来推导过程的基础。

在“可倒摆实验”中，当把摆锤正挂时，即将刀口E挂起时(文中加粗的量表示该量是矢量)，此时选择E所在的平面为零势能面。将摆拉动小角度放手，让摆做周期性摆动，此时关注两个特殊的位置，即“可倒摆”运动到最高点和最低点。当摆锤摆动到最低点时，由机械能守恒公式可得：

然后将摆锤倒挂时，由机械能守恒公式可得：

与单摆公式推导过程中使用的公式：sinθ≈θ不同，在本节中使用的小角近似公式为：

同时，将角速度的形势进行代换为：

此时，需要特殊说明的是：在“可倒摆实验”中需要保持正挂摆锤和倒挂摆锤时的周期近似相等，即T1≈T2。又由等时性原理可知，此时正挂和倒挂时的等效摆长一致。当等效摆长一致，保持正挂和倒挂的最大摆角一致时，两个过程中经过最低点时的角速度以及角速度的导数是一致近似的。所以，在接下来的推导中，为了进一步优化公式，本文将摆锤正挂和倒挂时的摆角、最低点角速度以及角速度的导数不作区分。

通过(10)和(11)进行化简操作，将(10)和(11)代入(8)和(9)，可得：

当最大对公式进一步地处理，对上两式进行时间求导可得：

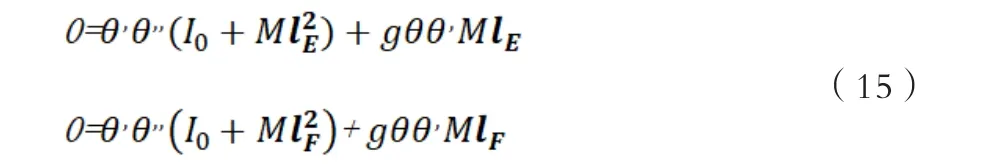
将其与(15)式中第一个公式联立可得：

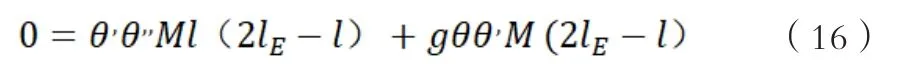
以上为实验原理推导过程。通过调节摆锤的位置可以实现实验正挂和倒挂的周期大致相等，即T1≈T2时。当正挂和倒挂的周期相等时，便可以通过实验数据使用(19)式来实验测出重力加速度g。在本节推导出的公式中所需要的实验限制条件是保持“可倒摆”正挂时和倒挂时的摆角一致，对原实验过程中|2h1-l|项同样进行要求。本文的实验中，在其他实验条件一致时，增加了实验限制，即保持正挂和倒挂的最大摆角一致。在定性上，这个限制减少了实验误差。

需要特别说明的是，上述推导过程中应用到的小角近似概念、摆的等时性概念（或者等效摆长概念）和转动惯量的平行轴定理都属于拓展知识点。对比两种推导过程，两者都提供了比较正确的思路，但后者是在前者的基础上进行另外一种思路的尝试。

在实验操作上，可以对比这个方法与传统方法。

相同点：两种方法都是通过测量等效摆长，摆的周期来计算重力加速度，且测量摆长和时间的仪器与方法都相同；实验约束条件中都需要保持“可倒摆”正挂和倒挂时的等时性T1＝T2以及|2h1-l|的值较大。

不同点：此方法的推导对于实验过程加了一个约束条件，即正挂和倒挂时最大摆角一致，减少了实验误差，可以较容易地实现T1＝T2。且此约束条件可以通过在实验过程中用铅垂线、角度尺或其他类似工具实现，操作起来并不难。

3 结语

“可倒摆实验”是用来测量重力加速度的一种非常巧妙的方法，减少了空气阻力的影响，极大地提高了实验的精确度。本文对转动惯量的推导部分进行了介绍，不同于传统通过复摆原理对“可倒摆实验”周期公式的推导，文中从能量的角度对其进行推导解释。关于其他的实验步骤，后者与前者与保持一致。另外，本文的方法增加了原实验限制条件，减少了实验误差。这种方式对于深入地理解“可倒摆实验”原理提供了一种新的思路，更便于从能量守恒的本质上理解该实验。同时，由于推导过程与单摆的周期公式推导过程存在紧密联系，一定程度上也增强了对复摆知识的理解。